Table of Contents
Uncertainty in observations
“Wrong ideas and theories are vital to science… Wrong data, on the other hand, are deadly.” — Chromey.
1. Accuracy and precision
“The alternative to divinity is variety.” — Chromey.
Accuracy and precision might sound synonymous in everyday language, but they are different in science. Accuracy is always less than Precision. Accuracy is the deviation from the true value which could be caused by systematic and stochastic errors. Systematic errors come from the instrument or atmosphere and will be the same for each trial or change with each trial in a predictable fashion. Stochastic error (random, accidental) will vary with each trial. Take the example set by Chromey in his book To Measure the Sky.
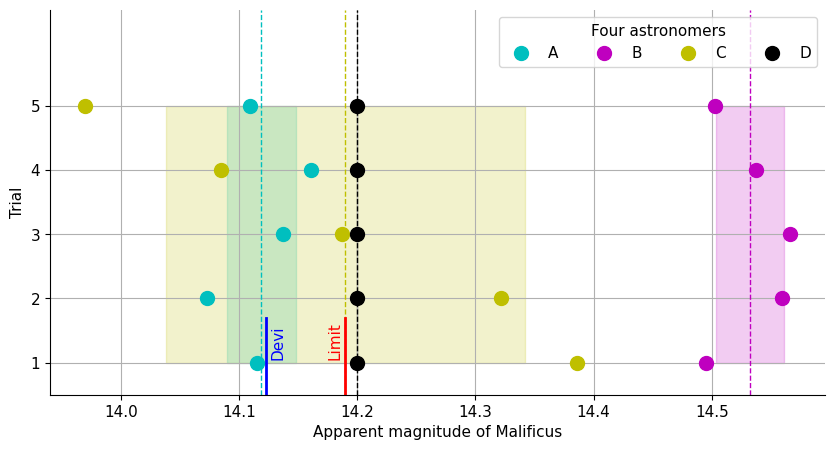
In the United Stars of Milky Way (USM) in the far far future, a smart theoretical astrophysicist determines that the star Malificus will soon implode and become a black hole killing the 10 million people living in the planet Magnificus orbiting the star completely unaware of their fate because they are still in the stone age. Astronomers of earth find out that if the apparent magnitude of the star is fainter (greater) than 14.190 by July 24 as seen from an Interstellar Space Station (ISS) orbiting Pluto, then the star will not implode and, hence, the Government of USM will not need to evacuate the people of Magnificus.
Four astronomers start taking data from the Plutonic ISS and a Devi comes to their assistance by giving them the accurate ‘true’ value: $14.123010$. So according to the Devi, the magnitude is smaller (brighter) than the limit and, hence, the star will implode, so the people should be evacuated asap. The crazy astronomers insist on measurements even after hearing this from the Devi. Each of them perform five observations (trials) and plot their data along with the divine value.
Each of them get 5 values. Which value to take as THE measured value of an astronomer. In this case, we are taking the average or mean, but there are other ways to take the actual value from multiple measurements, to be discussed later. Each astronomer can also determine the deviation of their individual measurements from this mean. They can either calculate spread as $x_L - x_S$ where $x_L$ and $x_S$ are the largest and smallest trial values, or the estimated standard deviation of the sample
$$ s = \left( \frac{1}{N-1}\sum_{i=0}^{N-1} |x_i-\overline{x}|^2 \right)^{1/2}. $$
Precision is often measured using just this $\sigma$, lower the standard deviation higher the precision. Accuracy is impossible to know because in reality devis do not help astronomers. But the accuracy can also be estimated from the precision. An imprecise value is seldom accurate.
| Astronomer | Precision | Accuracy | Decision |
|---|---|---|---|
| A (cyan) | Precise | Accurate | Evacuate |
| B (magenta) | Precise | Inaccurate | Stay |
| C (yellow) | Imprecise | Accurate | Uncertain |
| D (black) | Imprecise | Inaccurate | Uncertain |
Systematic errors are more important and dangerous for astronomy than stochastic errors. Astronomers A and B have the same precision, but after all the measurements B realizes that her values differ from the values of everyone else and, hence, unlikely to be true. Another reason for her inaccuracy is that her deviation from others is much greater than her precision. Astronomer C sees a systematic errors in his stochastic errors because his values decrease with time predictably.
A “result is useless until the size of its uncertainty is known.”
If $c$ is the true value and $u$ the uncertainty, than there is a 50% probability that the value will be $c\pm u$.
According to statistical theory, the uncertainty of the mean
$$ u = \frac{\sigma}{\sqrt{N}}. $$
Both A and B are confident because of their high precision and small uncertainty. They should confront each other. But C has enough precision (albeit very low) to cast doubt on B, but not enough to confirm A. There must be some systematic error separating A and B by such a large amount. They should spend all their energy to analyze their instrument and environment to find this systematic error.
What about D whose values are all the same? The problem with him is that he used an imprecise instrument that can only measure to the nearest 0.2 magnitudes. Because his instrument only measures every 0.2 magnitudes, he can say there is a 100% chance the true value is within $\pm 0.1$ of his mean. And there is a 50% chance that the value is within $\pm 0.05$ of his mean. In this case, the stochastic error is so small compared to the systematic error that it cannot be investigated at all.
The significant digits to quote will depend on the uncertainty.
- A’s result: $14.12\pm 0.013$.
- B’s result: $14.53\pm 0.013$.
- C’s result: $14.19\pm 0.07$.
2. Population and sample
A population contains all the measurements of a specific quantity, for example the life expectancy of the around 8 billion people of the world. A sample is a subset of the population taken for some specific purpose. The overall population can never be selected as it is too large. In almost all experiments of science, we select a sample, a subset from the population and try understand the characteristics of the overall population from the behavior of the selected sample.
Let us say I want to know the average (read ‘mean’) weight (read ‘mass’) of all Bangladeshis. I cannot measure the weight of all 170 million people. I have to choose a sample, and my estimate of the ‘average weight’ will be as good as my sample. If I select only chubby people, my estimate will skewed toward larger weight. If I select only skinny people, the estimate will be skewed toward smaller weight. To get a better estimate, I could select 100 people at random from all 64 districts of Bangladesh and then perform my statistics over the 6400 weights. This is what we do in astronomy as well, for example, while measuring the average of mass of stars in the Milky Way.
When I have multiple measurements of a quantity, I have to find a way to quote a single central or representative number based on all my measurements. Most of the times we use mean, but sometimes median and mode could be more meaningful. Let me introduce these terms in the context of a population.
The mean of a population
$$ \mu = \frac{1}{M} \sum_{i=1}^{M} x_i $$
where an individual member is denoted by $x_i$ and $i$ can range from $1$ to the total number of members $M$ in the population. The median $\mu_{1/2}$ is the middle value; as many members have values above the median as there are below, mathematically
$$ n(x_i\le \mu_{1/2}) = n(x_i\ge \mu_{1/2}) \approx \frac{N}{2}. $$
The mode $\mu_{max}$ is a third statistic giving the most common or frequent value.
$$ n(x_i = \mu_{max}) > n(x_i=y, y \ne \mu_{max}).$$
Let us say the following is the salary structure of the employees at a future company of the USM given in USD (United Stars Dollar) per year.
| Job title | Number of employees | Salary (thousand USD) |
|---|---|---|
| President | 1 | 2000 |
| Vice president | 1 | 500 |
| Software engineer | 3 | 30 |
| Astronomer | 4 | 15 |
There are 9 employees and the central values are as follows. Mean $\mu=294$ USD, median $\mu_{1/2}=30$ USD and mode $\mu_{\text{max}}=15$ USD. A capitalist would quote the mean, a socialist the median, but a communist would probably quote the mode.
Along with the central value, we will need to find a measure of the dispersion or scattering from the mean which will give the measure of uncertainty as well. The average of all the deviations from the mean is zero by the very definition of mean. The positive and negative deviations would be exactly equal and cancel each other. However, if we square all the deviations, the average will not be zero, but a reasonable estimate of the actual dispersion.
So the dispersion of a population is measured using the population variance
$$ \sigma^2 = \frac{1}{M} \sum_{i=1}^M (x_i-\mu)^2 = \frac{1}{M} \sum_{i=1}^M (x_i^2-\mu^2) $$
which tracks the spread of a dataset nicely. The square root of this number is the standard deviation of the population
$$ \sigma = \sqrt{\frac{1}{M} \sum_{i=1}^M (x_i-\mu)^2}. $$
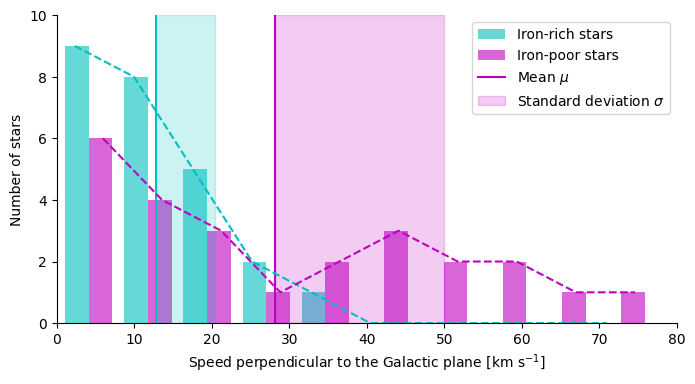
In this example, the velocities of 50 stars perpendicular to the Galactic plane are plotted as a bar-chart histogram. The stars are divided into two sets: 25 stars are iron-rich and the other 25 stars are iron-poor. The iron-poor stars have a greater dispersion of velocities as evident from the plot. The mean and the standard deviation are shown as vertical lines and shades, respectively.
Standard deviation is sometimes better than variance in describing physical phenomena because $\sigma$ has the same unit as $\mu$, but the units are squared in $\sigma^2$ statistic. In this example, the variance among iron-rich stars is $57.25$ km$^2$ s$^{-2}$ whereas the standard deviation is $7.57$ km s$^{-1}$.
In real life, we can never quite measure the whole population, but only a subset or sample of it. The mean of that sample $\bar{x}$ is not the same as the population mean $\mu$, but $\bar{x}$ approaches $\mu$ when the number of members in the sample $N$ is infinity or very large:
$$ \mu = \lim_{N\rightarrow \infty} \bar{x}, \ \text{ where } \ \bar{x} = \frac{1}{N} \sum_{i=1}^N x_i. $$
The sample variance similarly approaches population variance when $N$ is very large, but there is an important difference with the example of the mean as sample variance
$$ s^2 = \frac{1}{N-1} \sum_{i=1}^N (x_i-\bar{x})^2. $$
The factor $(N-1)^{-1}$ is very important; we are not dividing the variances by $N$ (number of samples from $M$) but by $N-1$. Again if $N$ is very large $N\approx N-1$, but $N\ne N-1$ if $N$ is small. One special case occurs when $N=1$ and this is exactly the case in cosmology. In cosmology, we have just one sample, the one universe. If $N=1$, then $(N-1)^{-1}$ becomes undefined and gives rise to the problem of cosmic variance. Wish we had more universes to sample from?
The standard deviation of the sample
$$ s = \sqrt{\frac{1}{N-1} \sum_{i=1}^N (x_i-\bar{x})^2} $$
which again approaches the standard deviation of the population $\sigma$ when $N$ is large.
3. Probability distributions
“The most important questions of life are, for the most part, really only problems of probability.” — Pierre-Simon Laplace
Because astronomical observations always select a sample from a given population (e. g. mass of 100 stars from 100 billion), it is important that we understand how to construct a sample from a population.
Imagine a jar full of metal balls with differing diameters. Stir up the jar and reach into it to take a ball without looking. This operation is called a ‘trial’ and the result of the trial is a ‘diameter’ $x$, a random variable. No matter how randomly you choose the balls, there is a function that describes the probability to get a diameter $x$ at a single trial. If the $x$ sample is taken from a population $Q$, then the function is $P_Q(x)$ called the probability distribution function because it gives the probability of finding the value $x$ at a single trial from a population $Q$.
Probability distributions can be continuous or discrete. Continuous distributions allow all integer and fractional values, but the discrete distributions allow only a discrete set of values. For the continuous case, $P_Q(x)(dx)$ is the probability of the value of $x$ being between $x$ and $x+dx$. And in the discrete case, $P_Q(x_j)$ is the probability of the value being $x_j$ where $j=1,2,3,...$
The probability distributions most used in astronomy are the discrete Poisson distribution and the continuous Gaussian distribution. Read the linked Universe articles for more about them.
Here instead let us compare the two. Poisson only allows non-negative integer values describing the number of events within a duration of time. For example, the number of raindrops falling on a tin-roof in one second, the number of photons falling on the detector of the Chandra X-ray telescope and so on. On the other hand, Gaussian distributions allow any positive or negative value and can describe the multiple measurements of any given quantity. For example, if you measure the magnitude of a star 100 times and get rid of all systematic errors, then the stochastic-error-dominated final results can be described using a Gaussian.
Gaussian is symmetric with respect to the mean $\mu$ and the standard deviation $\sigma$ is completely independent of the mean. Poisson is not symmetric and its variance is exactly equal to its mean: $\sigma^2=\mu$.
In case of Poisson, the fractional uncertainty $\sigma/\mu$ in measuring $N$ events is proportional to $N^{-1/2}$.
The Maxwell-Boltzmann distribution is another widely used function in physics and astronomy.
If a distribution $P(x,\mu,\sigma)$ is known, its mean and variance can be calculated easily. For the continuous case
$$ \mu = \frac{1}{N} \int_{-\infty}^{\infty} xPdx \text{ ; } \ \sigma^2 = \frac{1}{N} \int_{-\infty}^{\infty} (x-\mu)^2Pdx $$
and for the discrete case
$$ \mu = \frac{1}{N} \sum_{i=-\infty}^\infty x_i P(x_i) \text{ ; } \ \sigma^2 = \frac{1}{N} \sum_{i=-\infty}^\infty (x_i-\mu)^2 P(x_i). $$
4. Estimation
Estimation is the effort of determining the characteristics of a population based on some samples. The central limit theorem is the most important concept here, so try to focus on this first.
Let us go back to the example of a jar full of metal spheres. The spherical balls are made of iron and there are 10,000 of them in an enormous jar. A Devi plots the true distribution of the iron spheres as the left panel of the following figure.
As evident from the left panel, the distribution has two peaks at around 3 mm and 8 mm and it is not Gaussian as a whole even though the individual peaks look Gaussian. Now assign a demigod to reach into the jar and pick up 10 spheres, measure their diameters and calculate the mean. He then puts them back and again pick up 10 spheres blindly and repeat the procedure. This way he samples the population 1000 times and creates the right panel of the figure using the means of the 10 samples in each of the 1000 trials. Miraculously the distribution of the sample means look totally Gaussian. This miracle is called the central limit theorem.
5. Propagation
If an equation has multiple variables, the error associated with each variable will contribute toward the final error. So the errors have to be propagated from the right-hand side to the left-hand side of an equation. For example, differential photometry requires us to subtract one magnitude from another:
$$ \Delta m = m_1 - m_2 $$
where $m_1$ is the measured magnitude of a standard calibrator object and $m_2$ the magnitude of our designed unknown object. Now if $m_1$ has an error of $\sigma_1$ and $m_2$ has an error $\sigma_2$, then the final variance would be
$$ \sigma^2 = \sigma_1^2 + \sigma_2^2 $$
that is the variances do not get subtracted but add up. For both addition and subtraction, the errors will always add up. For multiplication and division, the rule is different. For example the ratio of the two corresponding fluxes
$$ F = \frac{F_1}{F_2} $$
will have an uncertainty related to the variance $\sigma^2$ as follows
$$ \left(\frac{\sigma}{F}\right)^2 = \left(\frac{\sigma_1}{F_1}\right)^2 + \left(\frac{\sigma_2}{F_2}\right)^2 $$
and again you see that whether there is a multiplication or division, the fractional errors always add up. The rule of error propagation can be generalized using the following way.
If $G$ if a function of $n$ variables ($x_i$) and their standard deviations are given by $\sigma_i$, then the variance in $G$ is given by
$$ \sigma^2 = \sum_{i=1}^n \left(\frac{\partial G}{\partial x_i}\right)^2 \sigma_i^2 + \mathcal{C} $$
where $\mathcal{C}$ is the covariance which we can consider zero for the current purpose. So we have to perform a partial differentiation of the function with respect to each variable $x_i$ and multiply the square of the result with the variance of that variable ($\sigma_i^2$). The rules of propagation for subtraction (addition) and division (multiplication) shown above can be derived from this.