— P R O B L E M S —

When light interacts with an object that is not large compared to the wavelength, the wave characteristic of light becomes important. Interference can only be described using light as a wave.

In geometric optics, we assumed light as particles and path of light as straight lines or rays. While discussing interference, we will have to talk about light as a wave and the corresponding field is called wave optics or physical optics.

The Dutch physicist Christiaan Huygens devised an useful technique for determining how light propagates as a wave.

Huygens’ principle states that every point on a wave-front is a source of wavelets that spread out in the forward direction at the same speed as the wave itself.

A plane wave is propagating toward right here. The plane created by the crests of all the waves at a particular position is called a wave-front. Each point on a wave-front is the source of another wave (wavelet) which travels to the right with speed $v$ which is the speed of the wave in this medium. If the new wave-front is created a time $t$ after the old wave-front, the radius of the wavelets $s=vt$.

Huygens principle can be used to describe all properties of light including reflection, refraction, dispersion, polarization and interference.

You can already see in the figure, wavelet produced by one point is interfering with the wavelet produced by another point. Two waves produced from a single wavefront can interfere destructively or constructively.

One way of creating two waves from one is by passing the wave through two slits as shown below.

Both the rays (described in geometric or ray optics) and the wavefronts (part of wave or physical optics) are shown here. The slits act as sources of coherent waves. Two waves are coherent if they have a constant phase relationship; that is if the phase difference of the two waves $\Delta\phi=|\phi_1-\phi_2|$ does not change with time.

Two coherent waves created by the two slits interfere and the resultant wave is detected by a screen as a pattern of bright and dark points called fringes. Points of constructive interference are bright and points of destructive interference are dark. In order to understand the separation among the fringes, let us describe the interference mathematically.

Two rays (back to that again!) $\mathbf{r}_1$ and $\mathbf{r}_2$ arising from $S_1$ and $S_2$, respectively, arrive at a point $P$ on on a screen.

The lengths $r_1$ and $r_2$ differ by a length $\Delta l$. Here $d$ is the distance between the slits, $D$ the distance from the slits to the screen and $\theta$ the angle of the paths with a line from the slits to the screen.

If $D>>d$, $\theta$ can be assumed to be the same for the two rays and, then, $\Delta l=d\sin\theta$.

If two waves are shifted by a wavelength $\lambda$, they will interfere constructively. If they are shifted by $\lambda/2$, they will interfere destructively. Here, the shift occurs due to the difference in path lengths $\Delta l$. If the order of the interference $m=0,\pm 1, \pm 2, \pm 3...$, then the condition can be generalized as follows.

For constructive interference, $\Delta l = d\sin\theta = m\lambda$.

For destructive interference, $\Delta l = d\sin\theta = (m+0.5)\lambda$.

Now consider the resultant waves on the screen. The intensities of the fringes fall off with distance $y$ from the central maximum fringe. If $\theta$ is small and the distance of the $m$-th order fringe from the central fringe is $y_m$, then $\sin\theta=\tan\theta=y_m/D$. Therefore, for constructive interference,

$$ d\frac{y_m}{D} = m\lambda \Rightarrow y_m = \frac{m\lambda D}{d}. $$

It turns fringes appear even after light passes through a single slit. This phenomenon is called diffraction. How are the two interfering waves created in this case?

To answer this, we can go back to the first figure of this page and observe that even a narrow wavefront will create many different wavelets from all its points and the wavelets can interfere at a later time.

Imagine many rays passing through a slit of size $a$ as shown below. Two wavelets shifted by a $\lambda$ will interfere constructively and $\lambda/2$ will interfere destructively, just as before.

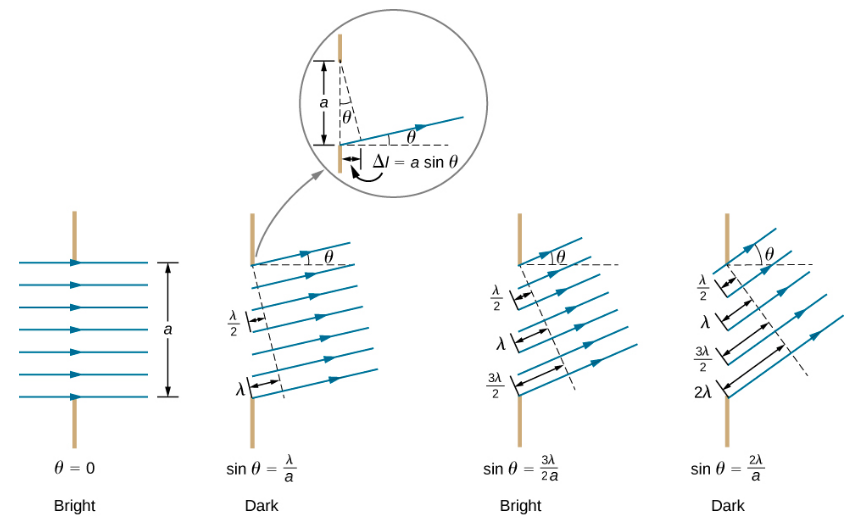
In the first figure to the left, the rays are parallel, $\theta=0$. In the next figure the ray at the bottom travels a distance $\lambda$ farther before reaching the same point on a screen as the ray at the top. So the ray through the center will have to travel a distance $\lambda/2$ shorter or larger than the rays at the bottom and top. So the interference between the rays at through the center and the edges of the slit will interfere destructively when path length difference $\Delta l=a\sin\theta=\lambda$. So the condition for having dark fringes become

$$ a\sin\theta = m\lambda $$

where $m$ is the order of the minimum in a diffraction pattern shown below (intensity as a function of $\sin\theta$).

The intensity of the central maximum is much higher than the other maxima on either sides. The central maximum is also much wider than the other maxima. The minima occurs where $\sin\theta$ is integer multiples of $\lambda/a$.