Table of Contents
3. Structure of a star
1. Equations of structure
1.1 Primary equations
The first of the equations was developed in Chapter 2. It is the equation of hydrostatic equilibrium given below.
\begin{equation}\label{1} \frac{dP}{dr} = -g\rho \end{equation}
where pressure $P(r)$, gravitational acceleration $g(r)$ and density $\rho(r)$ are all functions of radius $r$ of the star.1) This equation basically says, the net force on a volume element at any radius of a stable star should be zero. And $g(r)$ will only depend on the mass $M(r)$ of the star interior to the radius $r$.
The next equation gives the mass distribution and can be easily derived by considering a shell of thickness $dr$ at radius $r$ which will have a mass $dM=4\pi r^2 dr \rho$ because mass is volume times density. Dividing this by the thickness we get
\begin{equation}\label{2} \frac{dM}{dr} = 4\pi r^2\rho \end{equation}
which is the second of our differential equations. The third equation gives luminosity distribution $L(r)$ where the total luminosity $\mathcal{L}=L(R)$ if $R$ is the radius of the star. Note the difference between lowercase $r$ and uppercase $R$, the latter is the total distance from the center to the surface which is a constant while the former is a variable.
For deriving this, again consider the shell with mass $dM=4\pi r^2 dr \rho$ and multiply this with the energy generation function $\epsilon$ which has units W/kg. Note that $\epsilon(\rho,T)$ can be written only as a function of radius as $\epsilon(r)$ because density and temperature varies with radius. So $dL=dM\epsilon$ resulting in
\begin{equation}\label{3} \frac{dL}{dr} = 4\pi r^2\epsilon\rho \end{equation}
which is a statement of energy conservation. As mentioned in Chapter 2, the energy source function $\epsilon \propto \rho T^\beta$ where $\beta\approx 4$ for the pp chain and $\beta\approx 15$ for the CNO cycle.
The next equations are for the variation of temperature which depends on the radiative and convective transfer of heat inside a star. This is because the temperature is a measure of internal energy which changes due to heat transfer.
1.1.1 Radiative transfer
Consider two spherical surfaces at two different radii separated by one mean free path $\Delta r=(\kappa\rho)^{-1}$ where $\kappa$ is the opcaity in units of m$^2$ kg$^{-1}$, i. e. the cross-section for absorption and scattering per unit mass.

The two surfaces radiate toward each other as blackbodies with flux $\mathscr{F}=\sigma T^4$ where $\sigma$ is the Stefan-Boltzmann constant. The lower layer at radius $r_1$ has a higher temperature $T_1$. The net outward flow
$$ \mathscr{F} = \sigma T_1^4 - \sigma T_2^4 $$
in units of W m$^{-2}$. We have to multiply this by the surface area to get the luminosity $L(r)$ at a particular radius
$$ L = - 4\pi r^2 (\sigma T_1^4 - \sigma T_2^4) \approx -4\pi r^2 \Delta r \frac{d}{dr}(\sigma T^4) $$
because the $dr$ and $\Delta r$ nullify each other. Replacing $\Delta r=(\kappa\rho)^{-1}$ and taking the derivative, we find
$$ L = -16\pi\sigma r^2 \frac{1}{\kappa\rho} T^3 \frac{dT}{dr} \Rightarrow \frac{dT}{dr} = -\frac{1}{16\pi\sigma} \frac{\kappa\rho L}{T^3 r^2} $$
which is inaccurate by almost 30% because of our simplifying assumptions. The accurate equation for the temperature gradient in case of radiative transfer is
\begin{equation}\label{4} \dot{T}_r = \left.\frac{dT}{dr}\right\rvert_{\text{rad}} = -\frac{3}{64\pi\sigma} \frac{\rho}{T^3 r^2} L\kappa \end{equation}
which means high luminosity at some radius requires large temperature gradient across a length of $\Delta r$ at that radius. The temperature gradient is also proportional to opacity. The dependence of $dT/dr$ on $L$ and $\kappa$ is similar to Ohm’s law in electrical circuits. Comparing $\Delta T \propto L\kappa$ with $\Delta V=IR$, we see that luminosity is like current $I$, opcaity like resistance $R$ and temperature difference like the potential difference $\Delta V$.
1.1.2 Convective transfer

The temperature gradient also causes convective heat transfer by gas bubbles. Hot bubbles rise from lower to upper layers, become cool, sink down to lower levels and rise again upon absorbing heat, as shown above. This causes the surface of the sun (photosphere) to be fragmented into a lot of hot and cold regions called granules or convection cells.
This is a real highres video of the granular surface of the sun taken using the Daniel K. Inouye Solar Telescope (DKIST) located in Hawaii, USA. The average size of a granule is around $1''=1000$ km, almost the size of Iran.

Now, as shown above, again consider two spherical surfaces or layers at radii $r_1$ and $r_2$. As $\dot{T}_r$ is negative, temperature decreases with radius. Consider a bubble at $r_1$ with same density and temperature as its surroundings. If the bubble rises remaining in pressure equilibrium with its surroundings at every radius, it will expand and cool. if the rise is quick, we can ignore all heat exchange and consider the process to adiabatic, $\delta Q=0$.
If the bubble is cooler than its surroundings at $r_2$, it will be denser because the constant pressure $P\propto \rho T$. If it is denser, it will sink ending convection. But if the temperature of the bubble is higher than its surroundings at $r_2$, it will be lighter and keep rising, thus continuing the convection. So the condition of convection can be stated as
$$ \dot{T}_r = \left.\frac{dT}{dr}\right\rvert_{\text{rad}} > \left.\frac{dT}{dr}\right\rvert_{\text{ad}} = \dot{T}_a $$
where the subscript $\text{ad}$ stands for adiabatic convection. Stated in English, the radiative temperature gradient of the surroundings must be higher than the adiabatic temperature gradient of the bubbles, or the temperature of the bubbles should decrease less rapidly with radius than that of the surroundings. Because $\dot{T}_r\propto L$ whereas $\dot{T}_a$ is independent of luminosity, higher radial luminosity causes better convection.
Let us derive the expression for $\dot{T}_a$ using the expansion
$$ \left.\frac{dT}{dr}\right\rvert_{\text{ad}} = \frac{\partial T}{\partial P} \frac{dP}{dr} + \frac{\partial T}{\partial S} \frac{dS}{dr} = \frac{dT}{dP} \frac{dP}{dr} $$
where $S$ is entropy defined as $dS\equiv \delta Q/T$. The second term vanished because $dS/dr=0$ for an adiabatic process. The partial derivative could be replaced by total derivatives because temperature depends only on pressure through the relation $PV^\gamma=$ constant where $\gamma=C_P/C_V$. Here $C_P\equiv |\delta Q/dT|_P$ is the specific heat at constant pressure and $C_V\equiv |\delta Q/dT|_V$ is the specific heat at constant volume in units of J K$^{-1}$ mol$^{-1}$. Using $PV^\gamma=c_1$ and $PV=RT$ for one mole, it can be shown that
$$ \frac{dT}{dP} = \left(1-\frac{1}{\gamma}\right) \frac{T}{P} $$
and putting this in the expansion for $\dot{T}_a$ and remembering the expression for hydrostatic equilibrium, we see that
$$ \dot{T}_a = \left(1-\frac{1}{\gamma}\right) \frac{T}{P} (-g\rho) $$
which leads to the final form of the temperature gradient for convective transfer if we remember the EOS $P=\rho kT/m_{av}$ for non-degenerate gas:
\begin{equation}\label{5} \dot{T}_a = \left.\frac{dT}{dr}\right\rvert_{\text{ad}} = -\left(1-\frac{1}{\gamma}\right) \frac{m_{av}}{k} g \end{equation}
which is independent of luminosity as anticipated before.

In case of the sun radiative transfer is dominant up to $0.7 R_\odot$ and convective transfer is dominant in the outer $0.3 R_\odot$. In the outer parts, $L(r)$ does not vary with radius because nuclear burning is occuring far away at the core. So $\dot{T}_r\propto T^{-3}$ is mainly driven by the decreasing temperature toward the surface making it larger than $\dot{T}_a$ leading to convection.
1.2 Secondary equations
The five primary differential equations described the pressure, mass, luminosity and temperature gradients. There are two secondary equations that describe the states of the interior gas. The first one is just the ideal gas law:
\begin{equation}\label{6} P = \frac{\rho}{m_{av}} kT \end{equation}
where $m_{av}$ is the average mass of the particles in stellar gas, mainly protons and electrons. This equation depends on the chemical composition of the star via the mass. Actually four different quantities must be known as a function of density, temperature and composition ($\mathscr{C}$) for modelling a star using these equations:
- Average particle mass $m_{av}(\rho, T, \mathscr{C})$ in kg,
- Energy generation or source function $\epsilon(\rho, T, \mathscr{C})$ in W kg$^{-1}$,
- Opacity $\kappa(\rho, T, \mathscr{C})$ in m$^2$ kg$^{-1}$ and the dimensionless
- Ratio of specific heats $\gamma(\rho, T, \mathscr{C})$.
The chemical composition $\mathscr{C}$ is complicated. The opacity depends on the ionization state of the gas which can be calculated using the Saha equation (first derived by Meghnad Saha). It gives the degree of ionization of an atomic element in thermal equilibrium as a function of temperature and electron density:
\begin{equation}\label{7} \frac{n_{i+1}}{n_i} = \frac{G_{i+1}}{G_i} \frac{g_e}{n_e\lambda_e^3} e^{-E_i/(kT)} \end{equation}
where $n_i$ is the number density of atoms in the $i$th ionization state in units of m$^{-3}$. If $n_i$ is the density of atoms with 3 electrons missing, then $n_{i+1}$ is the density of atoms with 4 electrons missing. $n_e$ is the number density of electrons, $G_i$ is the partition function of the $i$th state, $g_e=2$ is the statistical weight of electron, $m_e$ is its mass, $E_i$ the ionization energy or the difference in energy between the levels $i$ and $i+1$ and, finally, the thermal de Broglie wavelength of electron
$$ \lambda_e = \sqrt{\frac{h^2}{2\pi m_e kT}} $$
where $h$ is Planck’s constant and $k$ the Boltzmann constant. For hydrogen $G_i\approx 2$, $G_{i+1}\approx 1$ and $E_i = 13.6$ eV.
2. Modeling a star
The seven equations given in Section 1, five primary and two secondary, are used to model a star. Ideally a mathematical model can be constructed using only two parameters: mass and chemical composition. Given these two, the model will automatically give the radius, luminosity and temperature. The radiative and convective zones will also be identified using the temperature gradients.
For modelling a spherical nonrotating star, $\kappa$ and $\epsilon$ are, first, determined independently from observation or theory. Then if the composition is considered uniform throughout the star, Eqn. \ref{6} can be used to eliminate $\rho$ from Eqns. \ref{1}–\ref{5}. Then the first five equations become single-variable resulting in $P(r)$, $M(r)$, $L(r)$ and $T(r)$. The boundary conditions $P(R)=0$, $M(0)=0$, $M(R)=\mathcal{M}$, $L(0)=0$ and $T(R)=0$ are specified. The solution of the first five differential equations are then carried out numerically using, for example, the Runge-Kutta methods.
One such modelling has been described in Appendix L of Introduction to Modern Astrophysics (edition 2) by Carroll and Ostlie and in this website by Michael Richmond. You have to use a python code to make a model of a star and postdict and predict its life. You can chose any type of star.
Stars are classified based on their effective temperature $T_e$ on the surface which is estimated from the absorption lines found in their spectra. The hottest to the coldest stars are assigned the spectral types O, B, A, F, G, K and M. O-type stars are divided into ten more types called by the numbers 0 to 9; B0 stars would be hotter than B9 stars. Stars also have a luminosity class given the Roman numerals I to VII. Class V stars are in the main sequence, meaning they are in hydrostatic equilibrium. Stellar classification is summarized below.
| Type | $M_V$ | $T_e$ [kK] | $M/M_\odot$ | $R/R_\odot$ |
|---|---|---|---|---|
| Main sequence stars (Class V) | ||||
| O3 | 120 | 15 | ||
| O5 | -5.7 | 42 | 60 | 12 |
| B0 | -4.0 | 30 | 17.5 | 7.4 |
| A0 | +0.65 | 9.79 | 2.9 | 2.4 |
| F0 | +2.7 | 7.3 | 1.6 | 1.5 |
| G0 | +4.4 | 5.94 | 1.05 | 1.1 |
| K0 | +5.9 | 5.15 | 0.79 | 0.85 |
| M0 | +8.8 | 3.84 | 0.51 | 0.60 |
| M8 | 0.06 | 0.10 | ||
| Giant stars (Class II) | ||||
| B0 | 20 | 15 | ||
| A0 | 4 | 5 | ||
| G5 | +0.9 | 5.05 | 1.1 | 10 |
| K5 | -0.2 | 4.05 | 1.2 | 25 |
| M0 | -0.4 | 3.69 | 1.2 | 40 |
| Supergiant stars (Class I) | ||||
| O5 | 70 | 30 | ||
| B0 | -6.5 | 28 | 25 | 30 |
| A0 | -6.3 | 9.98 | 16 | 60 |
| G0 | -6.4 | 5.37 | 10 | 120 |
| M0 | -5.6 | 3.62 | 13 | 500 |
Here $M_V$ is the absolute magnitude in visible wavelengths which is a dimensionless measure of luminosity. As you can see, the mass of main sequence stars can vary from 120 to 0.06 solar mass, but their radius varies from 15 to 0.10 solar radius. The variation in luminosity can be from 0.011 solar value to almost a million times more than the sun.

The models also provide the information about the radiative and convective zones inside a star. The lowest mass stars are completely convective and the size of central radiative zone increases with mass. In a solar-mass star only the outer envelope (30%) is convective, but a star becomes completely radiative if its mass is 1.5 solar mass. Stars more than two times heavier than the sun develop a convective zone at the core and the central convective zone keeps increasing in size with mass. So lightweight stars produce nuclear energy at the radiative core whereas heavyweight stars do that in their convective core.
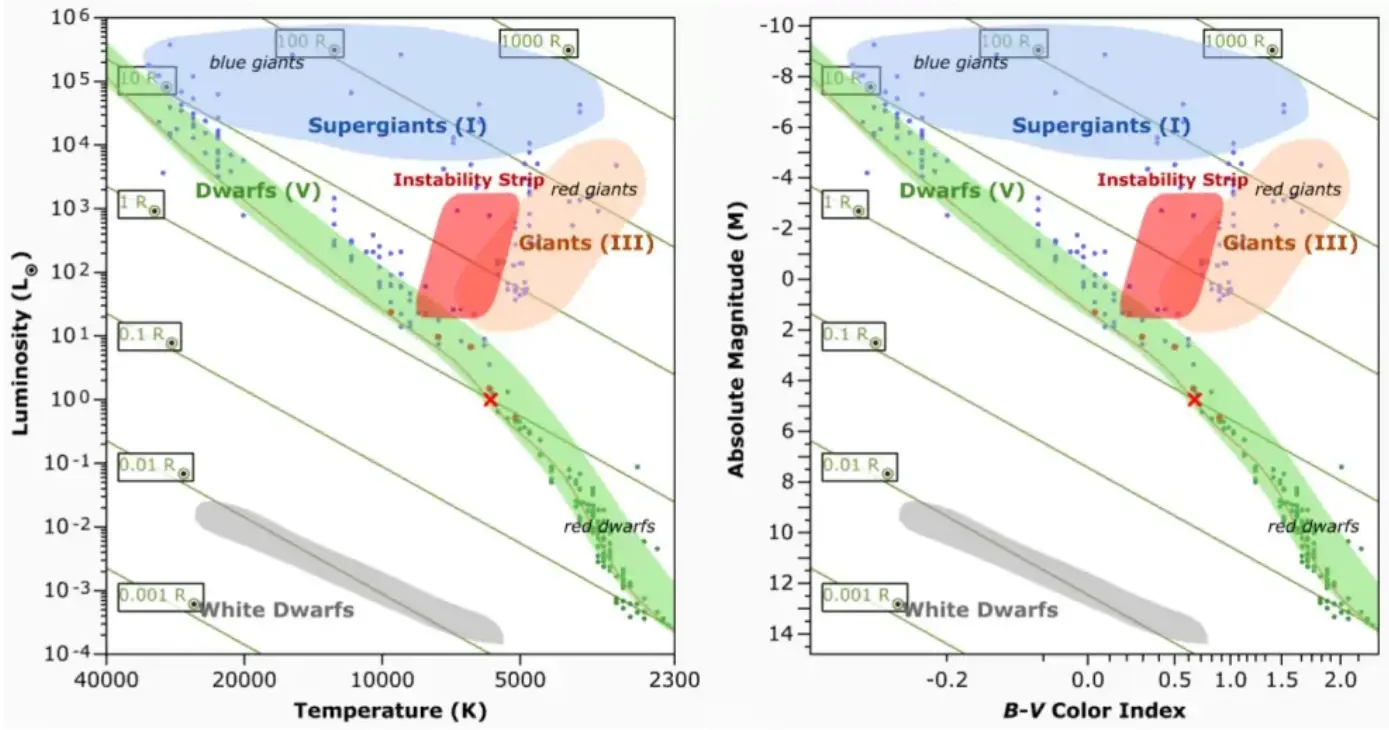
3. HR diagram
HR (Hertzsprung-Russell) diagram related the luminosity and temperature of stars. These two quantities are linked to the radius via the equation of flux we introduced before: $\mathscr{F}=\sigma T_e^4=L/(4\pi R^2)$ where $T_e$ is the effective temperature.
$$ R = \frac{\sqrt{L}}{\sqrt{4\pi\sigma}T^2} = \frac{\sqrt{L/L_\odot}}{(T/T_\odot)^2} \ R_\odot $$
which means there are diagonal constant-radius lines in the HR diagram. HR diagram can be shown using either $T$-$L$ or the corresponding observable quantities color index and absolute magnitude. Both temperature-luminosity and color-magnitude versions are shown below.
B-V color index is the difference between apparent magnitudes in the blue and visual or yellow bands, i. e. $m_B-m_V$. The absolute magnitude on the $y$-axis is the yellow magnitude $M_V$. A negative B-V index means the $m_B<m_V$ and, hence, the brightness in blue wavelengths is greater than in the visual band. Note that $M_V\propto - \log L$ and $(m_B-m_V)\propto -\log T$ which will be evident if you compare the axes of the two panels.
The green patch in the HR diagram is the main sequence where a star stays during its stable period. Before the birth a star is to the lower right hand side of the main sequence. When the equilibrium of the star is broken, it moves to the upper right hand side of the main sequence toward the giant (light red) or supergiant (blue) branches. After death stars move to the lower left hand side of the main sequence near the white dwarf patch (grey). Some massive stars oscillate periodically and they are found in the instability strip (dark red). On the main sequence the heavier stars are found in the upper part, and vice versa.