Stars like the Sun remain stable (do not expand or shrink) for almost 10 billion years. In this chapter, we will explore seven issues related to stars in equilibrium as listed below.

1. Condition for condensation
2. Requirement for equilibrium
3. Balance of kinetic and potential energies
4. Timescales for different changes
5. Nuclear reactions
6. Limiting luminosity
7. Instability and pulsations

Stars form from the condensation of gas cloud in the interstellar medium (ISM; see NASA Eyes). A condensing cloud must become dense enough for starting nuclear reactions. As a cloud condenses, it sheds angular momentum and must overcome the pressure of magnetic fields inherent in the ionized gas of the ISM.

Many bubbles of perturbation (higher density) can arise within a single cloud. The condition for such a perturbation to collapse (contract toward its own center) is simply that the magnitude of the gravitational potential energy ($E_p$) of an average atom in the cloud must be greater than its kinetic energy ($E_k$):

$$ E_k \lesssim |E_p|. $$

The average kinetic energy of an atom in a hydrogen cloud is around $(m_Hv^2)$ where $m_H$ is the mass of a hydrogen atom and $v$ its velocity. The magnitude of its gravitational potential energy is $(GMm_H/R)$ where $M$ is the mass of the cloud and $R$ its radius. Remembering from the definition of density ($\rho$) that $M\approx \rho R^3$, it can be demonstrated that a cloud will collapse if its size is greater than

$$ R \approx \frac{v}{\sqrt{G\rho}}. $$

It turns out the kinetic speed $v$ of particles in a gas is very close to the speed of sound $v_s$ in that gas. Thus we write Jeans length (click for full derivation)

$$ \lambda_J \approx \frac{v_s}{\sqrt{G\rho}}. $$

So the collapse is primarily dictated by density.

We can also find a critical mass or Jeans mass

$$ M_J \approx \left(\frac{kT}{Gm_{av}}\right)^{3/2} \frac{1}{\sqrt{\rho}} $$

which can be derived in two separate ways: either from the collapse criterion given in the beginning (replacing $mv^2\approx kT$) or from the Jeans length, replacing $v_s^2 = 5kT/(3m_{av})$. Try at home and derive in the class together. Always drop factors of order unity.

Calculate critical mass and length for the Cold Neutral Medium (CNM) of the ISM (the required values are given in the UV article) using Google Colab. What if the size of the cloud decreases hundred-fold? What is the critical mass and length in the intergalactic medium (IGM) where $n_H \sim 100$ m$^{-3}$ and $T\sim 3\times 10^4$ K?

In the CNM, Jeans length is around 60 ly, and Jeans mass more than 4000 $M_\odot$. As the CNM clouds are in reality less than 30 ly in size, they will not collapse. But if such a cloud would shrink hundred-fold, the critical mass would become only $3$ $M_\odot$. Large clouds become fragmented into many cloudlets. Each cloudlet can give rise to a star. A star cluster can form from a cloud.

For the IGM, critical mass can be almost $10^9$ $M_\odot$ which is the typical size of a galaxy.

A gas element with thickness $dr$ is at a distance $r$ from the center of a star. At this distance, the density of the gas is $\rho(r)$. If $dP=P_2-P_1$ is the pressure differential, then the net upward force on the element

$$ F_P = -A \ dP $$

where plus is outward from the center and vice versa. The condition for hydrostatic equilibrium is

$$ F_G + F_P = 0 \Rightarrow F_G = A \ dP. $$

The gravitational force on the mass element, $dm=\rho A \ dr$, would be

$$ F_G = \frac{-GM(r)\rho(r) A \ dr}{r^2} $$

where $M(r)$ is the mass within the radius $r$. Mass outside $r$ does not contribute to the force, which can be demonstrated using Gauss's law. Now replacing this force in the above equation yields

$$ \frac{dP}{dr} = \frac{-G M(r) \rho(r)}{r^2} = -\rho(r) g(r) $$

which is the most widely used form of hydrostatic equilibrium. Here the gravitational acceleration $g(r)=GM(r)/r^2$.

If a system of particles is in stable equilibrium bound by gravity, then the virial theorem relates its total kinetic and potential energy:

$$ 2\sum E_k + \sum E_p = 0. $$

So the total energy $E=0.5 \sum E_p = -\sum E_k.$ It is valid for any potential that varies inversely with distance, such as the gravitational potential.

A simple demonstration of the theorem comes from a satellite of mass $m$ orbiting the Earth of mass $M$ in a circular orbit of radius $r$. Its kinetic energy

$$ E_k = \frac{1}{2} mv^2 = \frac{1}{2} \frac{F_r}{a_r} v^2 = \frac{1}{2} \frac{GMm}{r^2} \frac{r}{v^2} v^2 = \frac{GMm}{2r} = - \frac{1}{2} E_p. $$

Total energy of a satellite decreases due to atmospheric drag. The satellite moves to lower radius, decreasing the potential energy in the negative direction (increasing in magnitude). As kinetic energy is opposite to potential energy, the kinetic energy increases and the satellite speeds up. But as kinetic energy is only half of the potential energy, the total energy still decreases.

Derive virial theorem from hydrostatic equilibrium.

If a star did not have any nuclear energy source, it would act like the satellite you saw above. Due to the loss of energy from the surface, it would shrink, $E_p$ would become more and more negative, $E_k$ would be increasing.

Temperature would rise due the increase in kinetic energy. Star heats up. The star is giving away more potential energy than is needed for decreasing the total energy, and the extra potential energy is getting converted to kinetic energy resulting in a higher temperature. The star has a negative specific heat as the removal of heat makes it hotter. This is a quasi-stable equilibrium.

The virial theorem works its magic only during the birth and death of a star. During the birth, the cloud shrinks, $E_k$ increases resulting in faster rotation, temperature increases resulting in higher pressure. The faster rotation opposes further shrinkage via centrifugal forces and the hotter gas opposes the same via higher outward pressure. The collapse may temporarily stop only to resume again when more energy and angular momentum is lost.

During the death, the star runs out of hydrogen for nuclear fusion at the center leading to the shrinkage of the core. As the core shrinks, it heats up leading to the optimum temperature for burning helium at the core. After helium runs, further shrinkage causes even heavier elements to be produced at the core.

But when a star is in a real equilibrium, the nuclear burning at its core produces as much energy as is lost from its surface in a year. And this is only ten millionth of the total energy of the sun. A star remains in hydrostatic equilibrium.

The image of the galaxy cluster SMACS J0723.3–7327 taken by JWST.

A cluster may have thousands of galaxies and much more intergalactic gas and dark matter. The total mass of a galaxy can be calculated using the virial theorem because clusters also obey the theorem. But there is a discrepancy.

The total kinetic energy of the cluster is calculated by measuring the mass and velocity dispersions of the member galaxies. Mass is measured from the luminosity. The total potential energy can be calculated by measuring the mass and position of the galaxies. Total $E_k$ should be half of total $E_p$, but we find that kinetic energy is much higher. There must be much more mass hidden somewhere in the cluster which is dubbed dark matter. More than 90% of the total mass of a cluster could be in the dark matter.

According to the virial theorem

$$ 2\sum_i \frac{1}{2} m_i v_i^2 - \sum_i \sum_{j \ne i} \frac{Gm_im_j}{r_{ij}} = 0. $$

If the cluster has $N$ identical galaxies each with mass $m$, then

$$ m \sum_i v_i^2 - G m^2 \sum_i \sum_{j \ne i} \frac{1}{r_{ij}} = 0. $$

Now multiply the first term by $N/N$ and the second term by $N^2/N^2$:

$$ Nm \left[\frac{1}{N} \sum_i v_i^2\right] - G \frac{(Nm)^2}{2} \left[\frac{1}{N(N-1)/2} \sum_i \sum_{j \ne i} \frac{1}{r_{ij}} \right] = 0 $$

where we assume $N(N-1)\approx N^2$ because $N$ is large. The factor $N(N-1)/2$ comes from the combination of two items from a total of $N$ items: $_NC_2=N!/[2!(N-2)!]=N(N-1)/2$. If total mass $M=Nm$ then

$$ M \langle v_i^2 \rangle_{av} - G\frac{M^2}{2} \langle r_{ij}^{-1} \rangle_{av} $$

and hence the virial mass of a cluster

$$ M = \frac{2\langle v_i^2 \rangle_{av}}{G \langle r_{ij}^{-1} \rangle_{av}}. $$

The velocities are calculated by measuring the line-of-sight (los) component of the velocity via Doppler shift. If all directions are equally probable, then all three components of the velocity vector can be considered equal. So

$$ \langle v_i^2 \rangle_{av} = 3 \langle v_{i,\text{los}}^2 \rangle_{av}. $$

The positions $r_{ij}$ must be corrected for projection effects.

Now that we can describe a star in equilibrium, we will check how long it takes for a star to change once its equilibrium is destroyed.

1. Thermal timescale is related to evolution in the absence of nuclear burning.
2. Dynamical timescale relates to the collapse of a star in the absence of equilibrium.
3. Diffusion timescale dictates the path of radiation from the center to the surface.

Another name for the Kelvin-Helmholtz timescale, which is the time it would take for a star to radiate away all its kinetic (thermal) energy as radiation. The thermal timescale

$$ \tau_k \approx \frac{\sum E_k}{L} $$

where $L$ is the luminosity (power) of the star. The kinetic energy is half the magnitude of the total potential energy and the total $E_p$ can be found by summing the potential energies of all the pairs of particles as in the example of galaxy clusters above. We can write

$$ \sum E_p = -2\sum E_k = -\frac{GM^2}{R} $$

where $M$ and $R$ are the mass and radius of the star, repsectively. So

$$ \tau_k \approx \frac{GM^2}{RL}. $$

If nuclear burning inside the sun sops today, it would take only around 30 My for the sun to radiate away all its energy and die. But we know that the sun is more than 4.5 Gy old because the age of earth is already 4.5 Gy. Therefore, there must be another source of energy inside the sun that is sustaining it for longer than the Kelvin timescale allows.

The timescale within which a star would collapse to its center if there was no outward opposing force. In order to derive this, assume a small test mass $m$ on the surface of a star of mass $M$ and radius $R$. If $g$ is considered constant (unrealistically) throughout the interior of the star, the inward radial acceleration of the mass

$$ a = \frac{F}{m} = \frac{GM}{R^2}. $$

The time needed to fall by a distance $R$ is found from the constant-force expression $s=at^2/2$, i. e. the dynamical timescale

$$ \tau_{in} = \sqrt{\frac{R}{a}} = \sqrt{R^3}{GM} $$

where density $\rho=M/R^3$ giving rise to

$$ \tau_{in} = (G\rho)^{-1/2}. $$

For the sun, density is around 1400 kg m$^{-3}$. So the time is around 50 minutes. It reduces to around 20 min if you consider the variation of density inside the sun.

A white dwarf with mass equal to the sun, but a size of only 1 per cent that of the sun would be almost a million times more dense than the sun. How quickly would it collapse? What about an even denser star with nuclear densities of around a billion kg per cubic meter?

The time it takes for a photon to reach the surface from the center. It takes time because of countless scattering and/or absorption-reemission (Thomson scattering). The timescale can be derived using a random walk.

Let us begin with a 1D photon random walk. Start the phtoton from $x=0$, flip a coin, move it to the right if the result is a head, to the left if it is a tail, always by a distance $\Delta x=l$. After 100 steps, $x\ne 0$ because of statistical fluctuation in the number of heads ($N_h$) and tails ($N_t$). If $N=N_h+N_t$ then

$$ x = Nl = (N_h-N_t)l $$

which is never zero. Averaging over many such 100-step trials would lead to an expected value of zero:

$$\langle x\rangle = \langle N_h-N_t \rangle l \approx 0$$

but the standard deviation (root-mean-square: rms) of $x$ is not zero. As the number of heads or tails follow Poisson distribution. If there are around 50 heads on average, $N_h=50$ and the uncertainty is $\Delta N_h = \surd{N}\approx 7$. So

$$ \Delta N = \sqrt{(\Delta N_h)^2+(\Delta N_t)^2} = \sqrt{N_h+N_t} = \surd N. $$

Even though the mean displacement is zero, the actual displacements will be distributed around the mean in a Gaussian distribution where the true displacement is the rms displacement

$$ x_{rms} = \sqrt{N} l. $$

For many 100-step trials, the photons go as far as $10l$, for 100-step trials $32l$, some in the one direction, some in another. Many photons start out from the center of a star. As time goes on, $N$ increases leading to a higher $x$. Plot various Gaussians here to understand this process of diffusion.

The number of photons required to reach a distance $x$ with $l$-sized steps:

$$ N\approx \left(\frac{x}{l}\right)^2. $$

In three dimensions,

$$ R_{rms}^2 = x_{rms}^2 + y_{rms}^2 + z_{rms}^2 = Nl^2 \Rightarrow N\approx \left(\frac{R}{l}\right)^2. $$

Factoring in the speed of a photon, we find the diffusion time

$$ \tau_{out} = \frac{Nl}{c} = \frac{R^2}{cl} $$

which cannot be calculated for the sun without knowing the typical step-size $l$ which is the mean free path, the average distance a photon remains free between any two collisions. It can be calculated from the Thomson cross section

$$ \sigma_T = \frac{8\pi}{3} r_e^2 $$

where the classical radius of an electron

$$ r_e = \frac{1}{4\pi\epsilon_0} \frac{e^2}{m_e c^2}. $$

The mean free path $l=(\sigma_T n_e)^{-1}$ where $n_e$ is the number density of scattering electrons, which is equal to the number of protons for a completely ionized gas. The mass is completely dominated by protons. So $n_e = \frac{M/R^3}{m_p}$. Thus we find

$$ l \approx \frac{m_p R^3}{\sigma_T M} $$

which results in

$$ \tau_{out} = \frac{\sigma_T}{cm_p} \frac{M}{R}. $$

For solar values, it is around 10 ky. The actual value is around 20 ky due to delays caused by absorption and emission.

The luminosity of the sun can be estimated from the diffusion time. Just divide the total amount of energy by the total diffusion time, to get the power in joules per s, or watts:

$$ L_\odot = \frac{aT^4 (4\pi R_\odot^3)/3}{\tau_{out}} \approx 10^{27} \text{ W} = 1 \text{ RW} $$

which is 1 ronna watts, or an octillion watts, or 1000 YK.

Photons have a thousand times less energy than the particles in the sun. So we need 1000 times more time to remove all energy of the sun if it was completely made of photons. A thousand times the diffusion timescale is indeed the thermal timescale.

The energy lost from the surface is in reality replaced by the energy produced via nuclear reactions at the core.

The stable equilibrium in a star is maintained by a negative feedback mechanism. If the star shrinks due to the excess of inward gravity over the outward pressure, temperature increases and nuclear energy output at the core increases due to higher particle flux and velocities. The increased energy causes the star to expand balancing the contraction due to gravity. On the other hand, if the star expands due to an excess of outward pressure over gravity, the temperature decreases reducing the nuclear energy output at the core causing the star to shrink balancing the expansion.

A star is mostly made of hydrogen which is completely ionized. So the star actually just have free protons and electrons. The main mechanism of nuclear burning is the proton-proton interaction. But it turns out the average kinetic energy of the protons is not high enough to overcome the Coulomb barrier that exists between the protons due to repulsive electromagnetic force. The kinetic energy is 1000 times less than required.

The solution is quantum tunneling. In the figures above $y$ axis is the energy of a proton and $x$ axis the distance to another approaching proton. The square-well shows the nuclear potential and the sloping sides the $r^{-1}$ Coulomb potential. Figure (a) shows the classical picture. The protons with kinetic energy $E_1$ and $E_2$ are unable to come close enough for the strong force to act, only the proton with $E_3$ can fall into the strong well classically. But protons do not have energy as high as $E_3$. Figure (b) shows quantum tunneling. At 10 MK, there are enough protons in the tail of the Maxwell-Boltzmann distribution for tunneling or leakage into the well.

Only 1 in 20 million photons can escape from the surface of the sun as radiation. So the nuclear energy has to replenish a very small amount of energy compared to the total thermal energy of a star. A star is not primarily a nuclear furnace, but a thermal furnace. The nuclear warmer of the sun has power of 400 YW (yotta watt) which is close the luminosity of the sun, 1000 YW.

Helium nuclei can be produced from hydrogen via the proton-proton or pp chain above about 5 MK. The core temperature of the sun is 1.6 MK. In the beginning, the sun had 71% H, 27% He and 2% heavier elements. Now, the amount of H at the core has been reduced to only 36%.

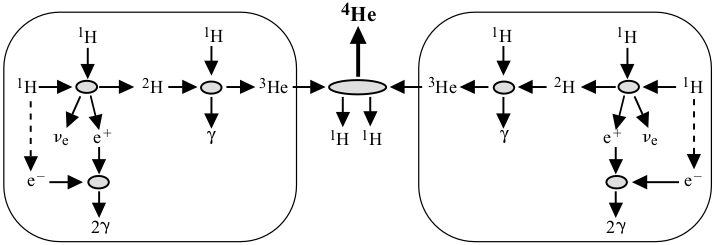
Neutrinos escape from the star. The electron and positron annihilate to create two gamma rays with energy $ E_{2\gamma} \approx 2m_e c^2 = 1.0 $ MeV. This and the motion of the deuterons contribute to the thermal energy of the star. Overall, six protons give rise to a $^4$He nucleus and two protons.

Number of baryons, leptons and charge must be conserved. We started with 6 baryons and end with 6 baryons (4 protons, 2 neutrons). We started with 6 leptons and end with 6 leptons (4 $e^-$ and 2 $\nu_e$). We started with net charge zero as there were exactly 6 protons and 6 electrons. In the end, the net charge is also zero as there are exactly 4 positive protons and 4 negative electrons left.

Conservation of energy must be true as well. In essence 4 HI atoms were converted to 1 HeI atom.

These are the less probable paths that the pp chain can take. The probability of each path is shown. THe pep process can also create deuterons, but contribute to only 0.4% of all $^4$He terminations. But the pep process emit a 1.44 MeV neutrino as opposed to just a 0.42 MeV neutrino of the pp process. Neutrino astronomers can detect the pep neutrino more easily. The highly improbable hep process creates an even higher-energy neutrino of 18 MeV.

The $\nu_e$ (standard model) from the sun is the main resource for neutrino astronomy. But only half of the expected neutrinos have been detected. The other half might have been transformed to other particles en route from the center to the surface of the sun.