কাসা ওয়ার্কশপ ১: মেঘে ঢাকা আর্টের হাজার চোখ
সেন্টার ফর এস্ট্রোনমি, স্পেস সায়েন্স এন্ড এস্ট্রোফিজিক্সের (কাসা) উদ্দেশ্য বাংলাদেশে এস্ট্রোনমির এমন একটা একাডেমিক প্রতিষ্ঠান বানানো যা আন্তর্জাতিক এস্ট্রোনমি কমুনিটির অংশ হবে। অন্য সব দেশে এস্ট্রোনমি যেভাবে কাজ করে এখানেও সেভাবেই করবে। দেশের বাইরের সাথে আমাদের কানেকশনের উপায় কাসা’র এসোসিয়েট মেম্বাররা, যাদের অনেকেই উত্তর আমেরিকায় ফ্যাকাল্টি বা পোস্টডক। তাদের সাথে আমরা দেশের ভিতরের ইউনিভার্সিটি স্টুডেন্টদের যোগাযোগ করিয়ে দিতে চাই, অর্থপূর্ণ ও প্রডাক্টিভ যোগাযোগ। কাসা হবে একটা কনফ্লুয়েন্স, যেখানে বিদেশের পুরাতন নদী এসে মিলবে দেশের নতুন নদীর সাথে, অতীতের ইনফ্লুয়েন্সে তৈরি হবে নতুন ভবিষ্যৎ।
দেশের বিভিন্ন ইউনিভার্সিটির স্টুডেন্টদেরকে এক জায়গায় এনে এস্ট্রোনমির আধুনিক বিভিন্ন মেথডের সাথে পরিচয় করিয়ে দেয়ার জন্য কাসায় থাকবে নিয়মিত ওয়ার্কশপ ও মিনিকোর্স। পাথফাইন্ডার হিসেবে আমাদের প্রথম ওয়ার্কশপ হয়েছে ২০২৫ সালের ২-৩ মে, ইনডিপেনডেন্ট ইউনিভার্সিটি, বাংলাদেশের (আইইউবি) মেইন একাডেমিক বিল্ডিঙের ছাদে কাসা অফিসে। বংলাদেশের ১৫টা ইউনিভার্সিটির মোট ৩০ জন স্টুডেন্ট দুই দিনের এই ওয়ার্কশপে লেকচার শুনেছে ও কাজ করেছে।
ওয়ার্কশপের বিষয় ছিল অ্যারে রেডিও টেলিস্কোপ (আর্ট), মানে অনেক এন্টেনার সমন্বয়ে বানানো রেডিও দুরবিন। বিষয়টা এমন হওয়ার কারণ আইইউবির ভিতরে বর্তমানে কাসা’র একমাত্র এস্ট্রোনমার আমি, আর আমার কাজের প্রধান বিষয় আর্ট। আমি নিজেকে রেডিও এস্ট্রোনমার বলি না, কারণ এক্স-রে এস্ট্রোনমি নিয়েও আমার কাজ আছে, আর বিভিন্ন কম্পাঙ্কের এস্ট্রোনমি মিলাতে না পারলে এই বিজ্ঞানের আসল আনন্দ পাওয়া যায় না। তবে ওয়ার্কশপের বিষয় আর্টে সীমাবদ্ধ রেখেছি কারণ সম্প্রতি কাসা অফিসের পাশে একটা ছোট আর্ট বানাতে গিয়ে রেডিও এস্ট্রোনমি নিয়ে আমাদেরকে অনেক ব্যস্ত থাকতে হয়েছে, এবং বেশি প্রস্তুতি ছাড়া স্টুডেন্টদের মধ্যে আমি যে বিষয়টার আনন্দ ছড়িয়ে দিতে পারব তা হলো রেডিও এস্ট্রোনমি।
ওয়ার্কশপের প্রথম দিন আমি তিনটা লেকচার দিয়েছি রেডিও এস্ট্রোনমি, আর্ট, ও রেডিও এন্টেনার বিম নিয়ে। পাশাপাশি স্টুডেন্টদেরকে চার-পাঁচ জনের মোট আটটা গ্রুপে ভাগ করা হয়েছে। বিকালে প্রত্যেক গ্রুপ তাদের প্রজেক্টের সেটাপ শুরু করেছে কাসা’র হাই-পারফর্মেন্স কম্পিউটিং (এইচপিসি) সার্ভারে, যার নাম টিমেয়াস। দ্বিতীয় দিন ভোরে একটা লেকচার দিয়েছি জের্নিকে পলিনমিয়ালের মাধ্যমে নেদারল্যান্ডের লোফার (লো ফ্রিকোয়েন্সি অ্যারে) টেলিস্কোপের একটা স্টেশনের বিম মডেল করা নিয়ে। বাকি দিন আট গ্রুপ এই মডেল নিয়েই কাজ করেছে। দিন শেষে প্রত্যেক গ্রুপকে তাদের রেজাল্ট প্রেজেন্ট করতে হয়েছে সবার সামনে।
এই লেখার উদ্দেশ্য দুই দিনের এই অভিজ্ঞতা একজন ইন্সট্রাক্টরের দৃষ্টিকোণ থেকে শেয়ার করা। পাশাপাশি লেকচারের বিষয়গুলোও এখানে সামারাইজ করব।
১। প্রথম দিন
কাসা ওয়ার্কশপ ১-এর জন্য এপ্লাই করেছিল প্রায় ১০০ জন। প্রাসঙ্গিক কোর্স, সিজিপিএ, এবং এপ্লিকেশনের আরো কিছু ক্রাইটেরিয়নের উপর ভিত্তি করে ৪৫ জনকে সিলেক্ট করেছিলাম। একটু সন্দেহ ছিল সবাই আসবে কি না, তবে ধরে নিয়েছিলাম ৪৫ জনের মধ্যে ৩০ জন আসলেই ওয়ার্কশপ সফল। আইইউবিতে সামার ২০২৪ ট্রিমেস্টারে আমার রেডিও এস্ট্রোনমি কোর্সে যে তিন জন ‘এ’ পেয়েছিল তাদেরকে রেখেছি ওয়ার্কশপের টিচিং এসিস্টেন্ট (টিএ) হিসেবে। দুই তারিখ সকাল ৯টায় কাসা অফিসে পৌঁছেছিলাম আমার বরাবরের সিক রুটিন মেনেই, মানে ৫ মিনিট লেইটে। সব সময় চাই ১০ মিনিট আগে পৌঁছাতে, কিন্তু হয়ে যায় ১০ মিনিট লেইট। গিয়ে দেখি ইতিমধ্যে অনেকে অফিসের সামনে অপেক্ষা করছে, দরজা বন্ধ থাকায় ঢুকতে পারেনি।
সকাল নয়টা থেকে দশটা ছিল আইসব্রেকিঙের সময়। সবাই আসবে, চা খাবে, একে অপরের সাথে পরিচিত হবে। হতাশ হতে হয়নি, সাড়ে নয়টার মধ্যেই বেশির ভাগ স্টুডেন্ট চলে আসে। প্রত্যেকের এরাইভাল টাইম গুগল শিটে লিখে রাখছিলাম। ত্রিশ জন চলে আসার পর প্রথমে ছয়টা গ্রুপ বানিয়ে ফেলি, প্রতি গ্রুপে থাকে পাঁচ জন স্টুডেন্ট। কিন্তু তারপর আরো প্রায় দশ জন আসে, গ্রুপ করতে হয় মোট ৮টা। আট গ্রুপ বসে অফিসের আটটা টেবিলে। আমি কাসা অফিসের ডিজাইন করেছিলাম ‘আমাদের কসমিক ইতিহাস’ কোর্সের কথা মাথায় রেখে। এই কোর্সে ৪০ জন স্টুডেন্ট থাকে যাদেরকে ৫ জনের ৮টা গ্রুপে ভাগ করা হয়, এবং পুরো ট্রিমেস্টারে জুড়ে এক গ্রুপের সবাই এক টেবিলে বসে, কারণ প্রত্যেক ক্লাসে লেকচারের পর গ্রুপওয়ার্ক করতে হয়। ক্লাসরুমের এই ডিজাইন ওয়ার্কশপের জন্যও কাজে লেগে গেলো।
১.১। রেডিও এস্ট্রোনমি
আইসব্রেকার শেষে সকাল দশটায় আমি রেডিও এস্ট্রোনমির বেসিক নিয়ে একটা এক ঘণ্টার লেকচার শুরু করি। বিষয় ছিল আলো, লাইট এমিশন ও ডিটেকশনের মেকানিজম, আলো মাপার ইউনিট, ইত্যাদি। আলোকে বর্ণনা করতে হয় ফোটন কণা হিসেবে এবং ইলেক্ট্রোম্যাগ্নেটিক ওয়েভ হিসেবে। হাই ফ্রিকোয়েন্সির এক্স-রে এস্ট্রোনমিতে আলোকে কণা হিসেবে বর্ণনা করা বেশি সুবিধাজনক, আর লো ফ্রিকোয়েন্সির রেডিও এস্ট্রোনমিতে তরঙ্গ হিসেবে। সুতরাং আলোর তরঙ্গ ধর্মটাই আমাদের ওয়ার্কশপের জন্য বেশি প্রাসঙ্গিক।
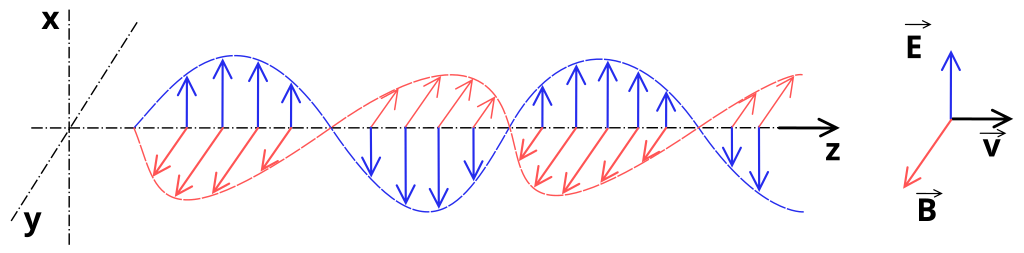
সব কম্পাঙ্কের এস্ট্রোনমাররাই আকাশের তলকে এক্স-ওয়াই প্লেইন হিসেবে চিন্তা করে, আর আকাশ থেকে দৃষ্টিরেখা বরাবর আসা আলোর দিক হয় জি এক্সিস। এক্স-ওয়াই প্লেইনে ইলেক্ট্রিক (ছবিতে $\mathbf{E}$, নীল) ও ম্যাগ্নেটিক ($\mathbf{B}$, লাল) ফিল্ডের অসিলেশনের কারণে যে তরঙ্গ তৈরি হয় তার বেগ ($\mathbf{v}$) জি এক্সিসের দিকে। আমি একটা দড়ির উদাহরণ অনেক ইউজ করি। একটা দড়ির এক প্রান্ত কোনো খুঁটিতে বেঁধে আরেক প্রান্ত ধরে যদি আমি উপরে-নিচে নাড়াই, তাহলে দড়ির মধ্য দিয়ে খুঁটির দিকে একটা তরঙ্গ প্রবাহিত হবে। আমার হাত যদি হয় ইলেক্ট্রিক চার্জ, তাহলে তরঙ্গটা হবে লাইট। হাত নাড়াচ্ছি এক্স-ওয়াই প্লেইনে, ওয়াই এক্সিস বরাবর, আর তরঙ্গ যাচ্ছে জি এক্সিস বরাবর। উপরের ছবিতে ইলেক্ট্রিক ফিল্ড অসিলেট করছে এক্স এক্সিস বরাবর, আর ম্যাগ্নেটিক ফিল্ড ওয়াই এক্সিস বরাবর। লাইটের ক্ষেত্রে ইলেক্ট্রিকের তুলনায় ম্যাগ্নেটিক ফিল্ডের মান এত কম হয় যে আমরা টেলিস্কোপ দিয়ে শুধু ইলেক্ট্রিক ফিল্ডটাই ডিটেক্ট করি।
প্রশ্ন হচ্ছে ইলেক্ট্রিক ফিল্ড অসিলেট করবে কেন? দড়িতে তরঙ্গ তৈরি হয় কারণ আমি হাত দিয়ে এক প্রান্ত নাড়াই। ইলেক্ট্রিক ফিল্ড লাইন যদি একটা দড়ির মতো হয়, তাহলে সেই দড়ির এক প্রান্ত ধরেও তো নাড়াতে হবে। কে নাড়াবে? উত্তর সোজা। ইলেক্ট্রিক চার্জ থাকলেই ইলেক্ট্রিক ফিল্ড লাইন থাকে। চার্জ থেকে অসীম পর্যন্ত ছড়ানো থাকে অসংখ্য ফিল্ড লাইন। চার্জের বেগ কন্সটেন্ট হলে এসব লাইনে কোনো তরঙ্গ থাকে না। কিন্তু চার্জের বেগ পাল্টালে, মানে তার এক্সিলারেশন (ত্বরণ) হলে, ফিল্ড লাইনের মধ্য দিয়ে তরঙ্গ প্রবাহিত হবে। চার্জ হলো উপরের উদাহরণে আমার হাতের মতো; দড়িতে তরঙ্গ তৈরির জন্য যেমন আমার হাত এক্সিলারেট করতে হয়েছিল, আলো তৈরির জন্য তেমনি চার্জ এক্সিলারেট করতে হয়। চার্জের এক্সিলারেশনই সব আলোর উৎপত্তির মূল কারণ।

সুতরাং কোনো এস্ট্রোনমিকেল অব্জেক্ট থেকে লাইটের এমিশন হতে পারে সেখানকার অনেক চার্জের ত্বরণের কারণে। তারপর সেই লাইট বা ইলেক্ট্রোম্যাগ্নেটিক তরঙ্গ আমাদের কাছে আসে এবং আমরা টেলিস্কোপ দিয়ে তা ডিটেক্ট করি। রেডিও দুরবিনের ক্ষেত্রে ডিটেকশন কিভাবে হয় তা উপরের ছবিতে দেখানো হয়েছে। যেকোনো দুরবিনের চারটা অংশ থাকে: কালেক্টর, ডিটেক্টর, প্রসেসর, ও মাউন্ট। কালেক্টর আলো প্রতিফলিত করে ফোকাল প্লেইনে নিয়ে যায়, ফোকাল প্লেইনে ডিটেক্টর আলোর ফোটনকে ইলেক্ট্রনে (চার্জ) কনভার্ট করে, বা বলা যায় ইলেক্ট্রিক ফিল্ড থেকে ইলেক্ট্রিক কারেন্ট তৈরি করে। প্রসেসর সেসব ইলেক্ট্রন বা কারেন্ট প্রসেস করে ফাইনাল ছবি বানায়। কালেক্টর ও ডিটেক্টরের সিস্টেমটা একটা মাউন্ট বা পেডেস্টালে বসানো থাকে। অনেক ক্ষেত্রে এই মাউন্টে একটা ড্রাইভ সিস্টেম থাকে যা কালেক্টর-ডিটেক্টর সিস্টেমকে কাঙ্ক্ষিত দিকে ঘুরাতে পারে। উপরের ছবিতে আমরা শুধু একটা সিম্পল ডিটেক্টর দেখতে পাচ্ছি, কারণ এটা বুঝাই ওয়ার্কশপের জন্য সবচেয়ে ইম্পর্টেন্ট।
রেডিও টেলিস্কোপের ডিটেক্টরকে অনেক সময় ফিড বলে। এক্স-ওয়াই প্লেইনের ইলেক্ট্রিক ফিল্ডের দুইটা কম্পোনেন্ট (এক্স ও ওয়াই) যদি আমরা স্বাধীনভাবে মাপতে পারি তাহলেই ফিল্ডের মোট মান বের করা যাবে। এজন্য ফিড থাকে দুইটা, এক্স ও ওয়াই। সবচেয়ে সিম্পল হচ্ছে ডাইপোল ফিড, যা হাইনরিখ হের্টস প্রথম বানিয়েছিলেন। উপরে শুধু ওয়াই কম্পোনেন্ট ডিটেক্ট করার ডাইপোলটা দেখানো হয়েছে। এরকম দুইটা ফিড একে অপরের সাথে পার্পেন্ডিকুলারভাবে থাকে এক্স-ওয়াই প্লেইনে, তাই এদেরকে একসাথে বলে ক্রস ডাইপোল। একটা ফিডে ফিল্ডের একটা কম্পোনেন্ট কিভাবে ধরা পড়ছে তা এনিমেশনে দেখানো হয়েছে। ফিল্ডের অসিলেশন ডাইপোলের দুই পাশে বিপরীত কারেন্ট তৈরি করছে; এজন্যই এর নাম ডাইপোল। এই কারেন্ট তৈরি হচ্ছে কারণ দুই পোলের মধ্যে একটা পটেনশিয়াল ডিফারেন্স আছে, যা ভোল্টেজ $V$ হিসাবে মাপা যায়। ভোল্টেজ ও কারেন্টের অনুপাত ওহমের সূত্র অনুযায়ী রেজিস্টেন্সের (R) উপর নির্ভর করে। এক্স আর ওয়াই ফিডের ভোল্টেজই রেডিও টেলিস্কোপের ডেটা; রেডিও দুরবিন আকাশের ভোল্টেজ মাপে।

এখানে লোফারের একটা হাই-ব্যান্ড এন্টেনা দেখানো হয়েছে। পার্পেন্ডিকুলার এক্স আর ওয়াই ফিড দেখা যাচ্ছে। এই দুই ফিডের ভোল্টেজকে যথাক্রমে $V_{xx}$ আর $V_{yy}$ বলা হয়। এক্স ফিড ইলেক্ট্রিক ফিল্ডের শুধু এক্স কম্পোনেন্ট ডিটেক্ট করার কথা, আর ওয়াই ফিড শুধু ওয়াই কম্পোনেন্ট, কিন্তু বাস্তবে এক্স ফিডেও ওয়াই কম্পোনেন্টের কিছুটা চলে আসে, আর ওয়াই ফিডে এক্স কম্পোনেন্টের কিছুটা। এই কারণে ভোল্টেজের আরো দুইটা কম্পোনেন্ট $V_{xy}$ আর $V_{yx}$ পাওয়া যায়; যাদের নাম ক্রস টক। এই চার কম্পোনেন্টকে একটা ২×২ জোন্স মেট্রিক্সে স্টোর করা হয়:
$$ \mathbf{V} = \begin{pmatrix}
V_{xx} & V_{xy} \\
V_{yx} & V_{yy}
\end{pmatrix}$$
যার প্রতিটা ভ্যালু কমপ্লেক্স নাম্বার। ইলেক্ট্রিক ফিল্ডের মান সব সময় রিয়েল, কিন্তু সময়ের সাথে পরিবর্তনশীল একটা ইলেক্ট্রিক ফিল্ডের সব তথ্য নিয়ে কাজ করতে হলে কমপ্লেক্স নাম্বার লাগে, কারণ এক তরঙ্গের সাথে আরেক তরঙ্গের ফেইজের পার্থক্য ইমাজিনারি পার্টে সংরক্ষিত থাকে। রিয়েল পার্ট যদি ফিল্ডের মান দেয়, তাহলে কমপ্লেক্স পার্ট দিবে তরঙ্গের ফেইজ, বা এরাইভাল টাইম। ফেইজ ডিলে বা টাইম ডিলে কেবল কমপ্লেক্স নাম্বারের মাধ্যমে স্টোর করলে হিসাব অনেক সহজ হয়ে যায়। সময়ের ($t$) সাথে পরিবর্তনশীল একটা ইলেক্ট্রিক ফিল্ড
$$ E(t) = E_0 \cos(\omega t + \phi) $$
যেখানে $E_0$ তার এমপ্লিচুড, $\omega$ হলো এঙ্গুলার ফ্রিকোয়েন্সি (ইউনিট রেডিয়ান / সেকেন্ড), আর $\phi$ ফেইজ। একেই কমপ্লেক্স নাম্বার হিসেবে আমরা লিখি
$$ \tilde{E}(t) = E_0 e^{i(\omega t + \phi)} $$
যেখানে $e^{i\omega t} = \cos(\omega t) + i\sin(\omega t)$, $e$ অয়লারের নাম্বার, আর $i=\sqrt{-1}$ ইমাজিনারি ইউনিট। রিয়েল নাম্বার দিয়ে কাজ করতে চাইলে এমপ্লিচুড ও ফেইজ আলাদাভাবে স্টোর করতে হয়, কিন্তু কমপ্লেক্স নাম্বার থাকলে এক নাম্বারের মধ্যে এমপ্লিচুড ও ফেইজের সব তথ্য নিয়ে আসা যায়। ওয়ার্কশপে একজন স্টুডেন্ট কমপ্লেক্স নাম্বারের বাস্তবতা নিয়ে ভালো প্রশ্ন করেছিল। ইলেক্ট্রিক ফিল্ড ও তাদের কারণে তৈরি ভোল্টেজ কি আসলেই কমপ্লেক্স, মানে তাদের মধ্যে কি আসলেই ইমাজিনারি নাম্বার আছে, নাকি কমপ্লেক্স নাম্বার এখানে কেবল হিসাবের সুবিধার্থে ইউজ করা হচ্ছে? যেকোনো একটা সময়ে ফিল্ড ও ভোল্টেজের মান রিয়েল, কিন্তু সময়ের সাথে তাদের ভেরিয়েশন কমপ্লেক্স নাম্বার ছাড়া ভালোভাবে বর্ণনা করা যায় না। কেউ বলতে পারে এমপ্লিচুড ও ফেইজ আলাদাভাবে স্টোর করলেই হয়, কমপ্লেক্স এনে ব্যাপারটাকে জটিল করার কি দরকার? আসলে কমপ্লেক্স নাম্বারের মাধ্যমে হিসাব এত সহজ হয় যে বাস্তবতাকে কমপ্লেক্স না ভেবে থাকা কঠিন। একটা এন্টেনার বদলে যখন অনেক এন্টেনার অ্যারের কথা আসে তখন কমপ্লেক্স নাম্বারের গুরুত্ব আরো বেশি বুঝা যায়, যা ছিল আমার পরের লেকচারের বিষয়।
তবে তার আগে আমি আলো মাপার ইউনিটের ধারণাটা নিয়ে এসেছিলাম যেকোনো দুরবিনের সবচেয়ে গুরুত্বপূর্ণ দুইটা প্যারামিটার বুঝানোর মাধ্যমে: রেজলুশন ও সেন্সিটিভিটি। টেলিস্কোপ কত ছোট জিনিস দেখতে পারে তা নির্ভর করে রেজলুশনের উপর, আর কত ফেইন্ট জিনিস দেখতে পারে তা নির্ভর করে সেন্সিটিভিটির উপর। সেন্সিটিভিটি একটা ফ্লাক্স হিসেবে দেয়া হয়। যেমন, সাউথ আফ্রিকার দুরবিন মিয়ারক্যাটের সেন্সিটিভিটি প্রায় ৫ মাইক্রো-জানস্কি, মানে ৫ মাইক্রোজানস্কির চেয়ে উজ্জ্বল যেকোনো অব্জেক্ট তার পক্ষে দেখা সম্ভব। কিন্তু জানস্কি কি জিনিস? জানস্কি রেডিও এস্ট্রোনমির সবচেয়ে মৌলিক ইউনিট, যার নাম রেডিও এস্ট্রোনমির অন্যতম ফাউন্ডার ইলেক্ট্রিকেল ইঞ্জিনিয়ার কার্ল জানস্কির নামে।
রেডিও আলো আমরা জানস্কি ইউনিটে মাপি, কারণ রেডিও আলোর তীব্রতা দৃশ্য আলোর চেয়ে অনেক কম। দৃশ্য আলোতে সূর্যের পাওয়ার যেখানে $10^{+26}$ W, সেখানে এক জানস্কি হলো $10^{-26}$ W m$^{-2}$ Hz$^{-1}$, খুবই কম। আমাদের আকাশে আনুমানিক ১ গিগাহার্জ কম্পাঙ্কে সূর্যের ফ্লাক্স ডেন্সিটি ১ মিলিয়ন জানস্কি পর্যন্ত হতে পারে, আর সূর্য ছাড়া আকাশের সবচেয়ে উজ্জ্বল রেডিও অব্জেক্ট ক্যাসিওপিয়া এ’র (ক্যাস এ) ফ্লাক্স ডেন্সিটি ১০০০ জানস্কি’র চেয়ে বেশি।
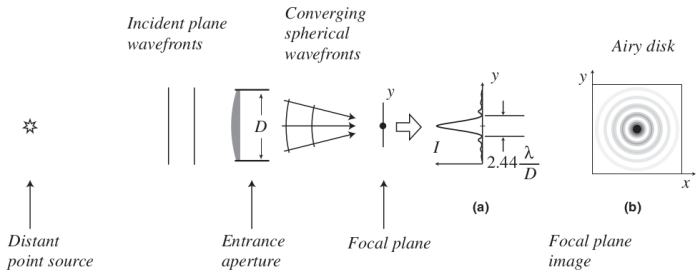
রেজলুশন বুঝানোর জন্য আমি ফ্রেডেরিক ক্রোমি’র বই থেকে নেয়া এই ডায়াগ্রাম সবখানে ইউজ করি; এখানে তারার মতো একটা পয়েন্ট-সোর্স থেকে টেলিস্কোপের এপার্চারে (এন্টেনার আরেক নাম) আলো আসার প্রসেস দেখানো হয়েছে। আকাশে সব তারা দেখতে বিন্দুর মতো, কিন্তু যেকোনো টেলিস্কোপ দিয়ে ছবি তোলার পরে ছবিটা দেখতে (b) প্যানেলের এয়ারি ডিস্কের মতো হয়। বিন্দু থেকে তরঙ্গের এই প্যাটার্ন হয় এপার্চারে আলোর ডিফ্রেকশনের কারণে। সহজ ভাষায় বললে, এপার্চারের দুই কোণায় আলো বেঁকে যায়, বা আলোর নতুন স্ফেরিকেল ওয়েভফ্রন্ট তৈরি হয়, এবং একাধিক ওয়েভের মধ্যে ইন্টারফেয়ারেন্সের কারণে ছবিটা দেখতে এয়ারি ডিস্কের মতো হয়। এই ডিস্কের একটা একমাত্রিক প্রফাইল (a) প্যানেলে দেখানো হয়েছে। এই ডিস্কের আরেক নাম পয়েন্ট স্প্রেড ফাংশন (পিএসএফ), এবং এর মাঝখানের মেইন লোবের রেডিয়াসকে বলে রেজলুশন ($\alpha$)।
মিয়ারক্যাটের রেজলুশন অনেক সময় ৫ আর্কসেকেন্ড (১ ডিগ্রির ৩৬০০ ভাগের এক ভাগ হলো ১ আর্কসেকেন্ড) হতে পারে। মানে মিয়ারক্যাট দিয়ে তারার মতো একটা বিন্দুর ছবি তুললে ছবিতে যে এয়ারি ডিস্ক দেখা যাবে তার মেইন লোবের এঙ্গুলার রেডিয়াস ৫ আর্কসেকেন্ড। তাহলে কোনো অব্জেক্টের সাইজ আমাদের আকাশে যদি ৫ আর্কসেকেন্ডের কম হয়, মিয়ারক্যাটের পক্ষে সেই অব্জেক্টকে তার আশপাশের ব্যাকগ্রাউন্ড থেকে আলাদা করা সম্ভব হবে না, মানে মিয়ারক্যাট তাকে রিজল্ভ করতে পারবে না। এজন্যই এর নাম রেজলুশন। (a) প্যানেল থেকে দেখা যাচ্ছে এয়ারি ডিস্ক বা পিএসএফের মেইন লোবের রেডিয়াস
$$ \alpha = 1.22 \frac{\lambda}{D} $$
যা $\lambda$ তরঙ্গদৈর্ঘে $D$ ব্যাসের একটা দুরবিনের রেজলুশন। দুরবিনের কালেক্টরের ব্যাস যত বাড়ানো হয়, $\alpha$ তত কমে, মানে রেজলুশন তত ভালো হয়। কিন্তু রেডিও তরঙ্গের ওয়েভলেন্থ অনেক বেশি বলে রেডিও দুরবিনের রেজলুশন বাড়াতে হলে ব্যাস অনেক হতে হয়। পৃথিবীর সবচেয়ে বড় অপ্টিকেল দুরবিনের ব্যাস ১০.৪ মিটার, আর ৬০০ টেরাহার্জ কম্পাঙ্কে তার রেজলুশন ০.০১ আর্কসেকেন্ড। কিন্তু সবচেয়ে বড় সিংগল-ডিশ রেডিও দুরবিনের ব্যাস ৫০০ মিটার, তাই ১৫০০ মেগাহার্জে তার রেজলুশন প্রায় ৮০ আর্কসেকেন্ড। রেডিওতে ৫০০-মিটার কালেক্টর দিয়েও অপ্টিকেলের মাত্র ১০-মিটার কালেক্টরের সাথে পাল্লা দেয়া যায় না। তাই রেডিওতে রেজলুশন বাড়ানোর একমাত্র উপায় অনেক দূরে দূরে রাখা অনেক এন্টেনার অ্যারে। কারণ সেক্ষেত্রে রেজলুশন একটা সিঙ্গেল এন্টেনার ব্যাসের উপর নির্ভর করে না, নির্ভর করে সবচেয়ে দূরের দুইটা এন্টেনার মধ্যে দূরত্বের উপর।
১.২। অ্যারে রেডিও টেলিস্কোপ (আর্ট)
একটা টি-ব্রেকের পর আমি সবাইকে একাধিক এন্টেনার অ্যারে বুঝানোর চেষ্টা করি। কাসা অফিসের বাইরে আমরা স্মল ট্রানজিয়েন্ট অ্যারে রেডিও টেলিস্কোপ (স্টার্ট) নামে একটা অ্যারে ডিপ্লয় করছিলাম তখন। ফ্যাব ল্যাবের শোয়েব তখনো বাইরে কাজ করছিলেন। এটা ২৪টা এন্টেনার অ্যারে, কিন্তু ওয়ার্কশপে আমরা নেদারল্যান্ডের লোফার দুরবিন নিয়ে কাজ করেছি, যার হাই-ব্যান্ড এন্টেনার সংখ্যা প্রায় ৫০ হাজার। দুই এন্টেনার কম্বিনেশনকে বলা হয় ইন্টারফেরোমিটার, এবং এমন অনেক ইন্টারফেরোমিটার মিলে হয় একটা অ্যারে।
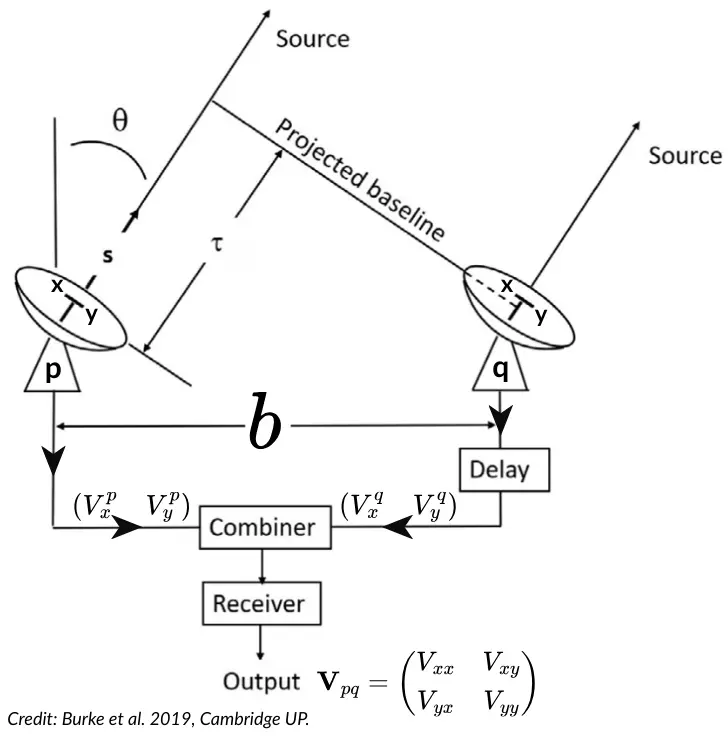
ধরা যাক দুইটা এন্টেনা $p$ আর $q$ আকাশের কোনো সোর্স থেকে ভার্টিকেল দিকের (জেনিথ) সাথে $\theta$ এঙ্গেলে আসা আলো অব্জার্ভ করছে। আলো আগে পৌঁছাবে কিউ-তে, এবং তার $\tau$ সময় পর পি-তে। এই সময়ের পার্থক্য যদি দূর করতে চাই, তাহলে কিউ এন্টেনার অব্জার্ভেশনের সাথে একটা টাইম ডিলে যোগ করতে হবে। দুই এন্টেনার ফোকাল প্লেইনেই এক্স ও ওয়াই ফিড আছে। কম্বাইনারের কাজ দুই এন্টেনার এক্স ও ওয়াই ফিডের ভোল্টেজ কোরিলেট করে রিসিভারে পাঠানো। রিসিভারে শেষে যে ডেটা তৈরি হবে তার নাম ভিজিবিলিটি $V_{pq}$ যা $b$ দূরত্বে (যার নাম বেসলাইন) থাকা দুই এন্টেনার অব্জার্ভেশনের কোরিলেশন। এটাও আগের মতো জোন্স মেট্রিক্স, কিন্তু এর প্রত্যেক এলিমেন্ট দুই এন্টেনার ডেটার কোরিলেশন। অর্থাৎ এখানে $V_{xx}$ হলো পি এন্টেনার এক্স ফিডের সাথে কিউ এন্টেনার এক্স ফিডের ভোল্টেজের ক্রস-কোরিলেশন।
নেদারল্যান্ডের পিটার হেন্ড্রিক ভান সিটার্ট এবং ফ্রিটস জের্নিকে ১৯৩০-এর দশকে আবিষ্কার করেছিলেন যে, কিছু শর্তসাপেক্ষে অনেক দূরের কোনো সোর্স থেকে আসা আলোর ইন্টেন্সিটি ডিস্ট্রিবিউশনের ফুরিয়ে ট্রান্সফর্ম সেই আলোর কমপ্লেক্স ইন্টারফেরোমেট্রিক ভিজিবিলিটি’র সমান। তার মানে দুই এন্টেনার একটা বেসলাইন থেকে পাওয়া কমপ্লেক্স ভিজিবিলিটি আকাশের সরাসরি ফুরিয়ে ট্রান্সফর্ম। অর্থাৎ একটা ইন্টারফেরোমিটার আসলে সরাসরি আকাশের ছবি তোলে না, বরং স্যাম্পল করে আকাশের ফুরিয়ে ট্রান্সফর্ম। যেকোনো ছবি বা সিগ্নালকে অনেক ফ্রিকোয়েন্সি ও এমপ্লিচুডের অসংখ্য সাইন ও কোসাইন ফাংশন দিয়ে বর্ণনা করার নাম ফুরিয়ে ট্রান্সফর্ম। নির্দিষ্ট ফ্রিকোয়েন্সি ও এমপ্লিচুডের একটা সাইনুসয়ডাল ফাংশনকে বলতে পারি একটা ফুরিয়ে মোড। একটা বেসলাইন আকাশের একটা ফুরিয়ে মোড ডিটেক্ট করে। আর্টের মাপা কমপ্লেক্স ভিজিবিলিটি যে সমীকরণের মাধ্যমে বর্ণনা করা হয় তার নাম রেডিও ইন্টারফেরোমেট্রি মেজারমেন্ট ইকুয়েশন (রাইম):
$$ \mathbf{V}_{pq}(u,v) = \iint_{l,m} \mathbf{B}_p \ \mathbf{E}(l,m) \ e^{-2\pi i(ul+vm)} \ \mathbf{B}_q^H \ dl \ dm $$
যেখানে $l,m$ আকাশের কোওর্ডিনেট, বিভিন্ন দিকে রাইট এসেনশন ও ডেক্লিনেশনের কোসাইন, $u,v$ পৃথিবীর পৃষ্ঠে আর্টের একটা বেসলাইনের কোওর্ডিনেট, $\mathbf{B}$ একটা সিঙ্গেল এন্টেনার বিম, মানে বিভিন্ন দিকে এন্টেনার সেন্সিটিভিটি, এবং $^H$ মানে হার্মিশিয়ান কনজুগেট বা এডজয়েন্ট। আকাশে আমাদের লক্ষ্যবস্তুর ব্রাইটনেস মেট্রিক্স
$$ \mathbf{E} = \begin{pmatrix} E_{xx} & E_{xy} \\
E_{yx} & E_{yy}
\end{pmatrix}$$
যেখানে $E_{xx}$ আকাশ থেকে আসা ইলেক্ট্রিক ফিল্ডের এক্স কম্পোনেন্টের অটো-কোরিলেশন। এখানে রাইমের দ্বিমাত্রিক ভার্সন দেয়া হয়েছে, এবং এই ভার্সনে আসমানের সাথে জমিনের ফুরিয়ে সম্পর্ক একদম পরিষ্কার। কিন্তু বেসলাইনের কোওর্ডিনেট বুঝতে হলে, ইউ-ভি প্লেইন ও ইউ-ভি কাভারেজ বুঝতে হবে, এবং সেজন্য আমাদেরকে দুই এন্টেনার ইন্টারফেরোমিটারের বদলে অনেক এন্টেনার অ্যারে নিয়ে ভাবতে হবে। ওয়ার্কশপে অ্যারে কনফিগারেশন আমি ফ্রেন্ডলি ভিআরআই নামে একটা সফটওয়ার দিয়ে দেখিয়েছি, এখানেও তাই করব। এটা দিয়ে পৃথিবীর সবচেয়ে বড় বেশ কিছু আর্টের মক অব্জার্ভেশন সিমুলেট করা যায় ছোট স্কেলে।

এখানে আমি ইন্ডিয়ার জায়ান্ট মিটারওয়েভ রেডিও টেলিস্কোপ (জিএমআরটি) সিলেক্ট করেছি অব্জার্ভেশনের জন্য। এই আর্টে ৩০টা প্যারাবলিক মেশ এন্টেনা আছে ওয়াই কনফিগারেশনে, একেকটার ব্যাস ৪৫ মিটার। এন্টেনাগুলির পজিশন উপরে বাম কোণায় দেয়া আছে, যেখানে এক্স এক্সিসে আছে পূর্ব-পশ্চিম বরাবর আপেক্ষিক দূরত্ব কিলোমিটারে, আর ওয়াই এক্সিসে উত্তর-দক্ষিণ বরাবর দূরত্ব। আওয়ার এঙ্গেল রেঞ্জ সিলেক্ট করেছি -৪ থেকে +৫ পর্যন্ত, মানে প্রায় ১১ ঘণ্টার অব্জার্ভেশনের সেটাপ করা হয়েছে। এরপর মডেল ইমেজ হিসেবে সিলেক্ট করেছি একটা রেডিও গ্যালাক্সির ছবি, যার মাঝখানের ব্ল্যাকহোল থেকে দুইটা লোব বের হয়েছে। এখানে গ্যালাক্সির বদলে আমার ছবি দিলেও চলত। এই সফটওয়ার যেকোনো ছবি একটা আর্ট দিয়ে অব্জার্ভ করলে কেমন দেখাবে তা বের করে দেয়। ৩০ টা এন্টেনা থেকে মোট ৩০ × ২৯ / ২ = ৪৩৫ টা ইউনিক পেয়ার পাওয়া যায়। প্রতিটা পেয়ার একটা বেসলাইন।
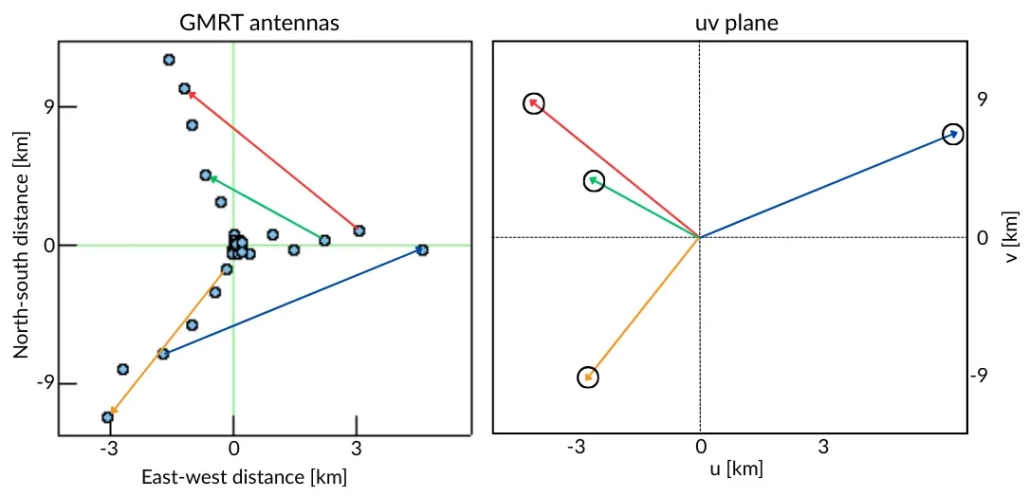
প্রতিটা পেয়ারের বেসলাইনকে একটা ভেক্টর হিসাবে চিন্তা করা যায়। উপরে চারটা ভেক্টর দেখানো হয়েছে। এই সব ভেক্টরকে একটা কমন অরিজিনে ট্রান্সলেট করলে যে প্লেইন পাওয়া যায় তার নাম ইউভি প্লেইন, কারণ তার এক্স এক্সিস ইউ, ওয়াই এক্সিস ভি। এই কোওর্ডিনেটই রাইমে ইউজ করা হয়েছে। একটা ভেক্টরের টিপ জানলেই তার দিক ও দৈর্ঘ্য জানা সম্ভব, তাই শুধু টিপগুলো সার্কেল দিয়ে দেখানো হয়েছে ছবির ডান প্যানেলে। এখন শুধু টিপ রেখে যদি ভেক্টরের লাইনগুলো বাদ দেই, তাহলে প্রতিটা টিপের ট্র্যাক বুঝা সহজ হবে। পৃথিবী যেহেতু ২৪ ঘণ্টায় একবার ঘুরছে, সেহেতু আকাশের একটা অব্জেক্টের সাপেক্ষে এই প্রত্যেকটা টিপ ২৪ ঘণ্টায় একটা কমপ্লিট এলিপ্স তৈরি করবে। আমাদের যেহেতু ১১ ঘণ্টার অব্জার্ভেশন, সেহেতু প্রত্যেক টিপের জন্য একটা এলিপ্সের প্রায় অর্ধেক পাওয়া যাবে।
এভাবে এগার ঘণ্টায় ইউভি প্লেইনে যে প্যাটার্ন তৈরি হয় তার নাম ইউভি কাভারেজ, যা নিচের ছবিতে উপরের সারির মাঝখানের প্যানেলে দেখা যাচ্ছে; ফ্রেন্ডলি ভিআরআই-এ “ডু অব্জার্ভেশন” বাটনে ক্লিক করলে নিচের ছবিগুলো তৈরি হয়।
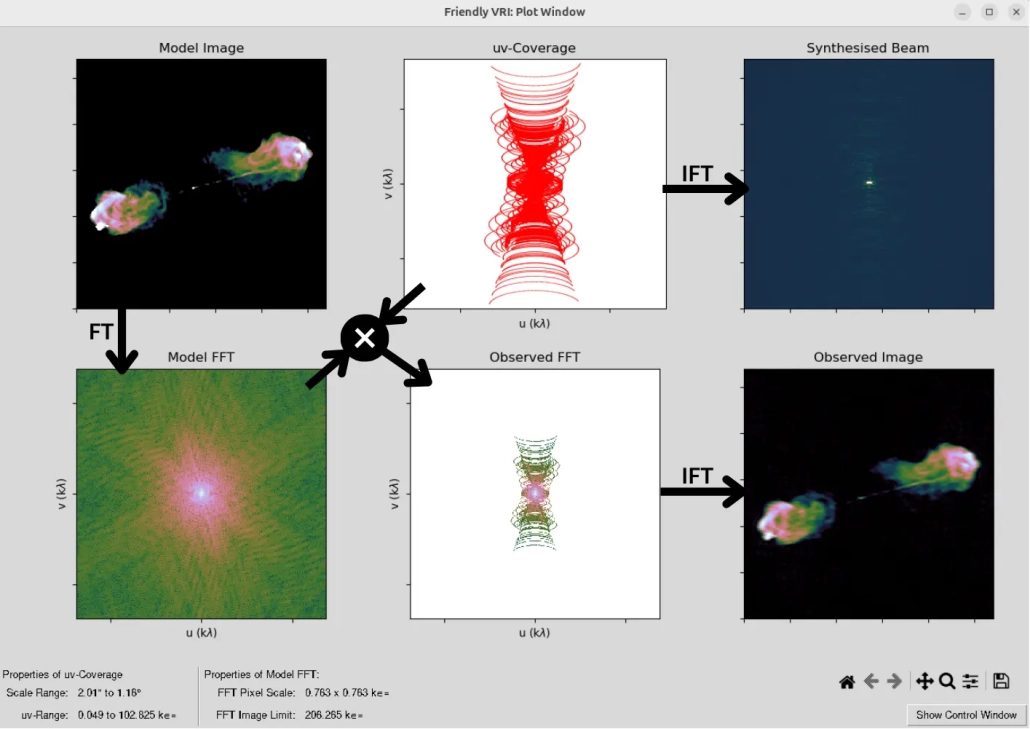
এই ছবিতে ফ্রেন্ডলি ভিআরআই-এর সিমুলেশনের প্রতিটা ধাপের ছবি আছে। মডেল ইমেজ হচ্ছে কাঙ্ক্ষিত অব্জেক্ট যার ছবি তুলতে চাচ্ছি আর্ট দিয়ে। এটার ফুরিয়ে ট্রান্সফর্ম হলো নিচের মডেল এফএফটি (ফাস্ট ফুরিয়ে ট্রান্সফর্ম)। মডেল এফএফটি’র সব ফুরিয়ে মোড আমাদের আর্ট স্যাম্পল করতে পারবে না, যেটুকু পারবে তা পাওয়া যাবে মডেল এফএফটি এবং ইউভি-কাভারেজ গুণ করলে। ফুরিয়ে প্লেইনে দুইটা জিনিস মাল্টিপ্লাই করলে আসলে যে অপারেশনটা হয় তার নাম কনভলুশন। এই কনভলুশনের রেজাল্ট হচ্ছে আমাদের অব্জার্ভড এফএফটি, যাকে ইনভার্স ফুরিয়ে ট্রান্সফর্ম (আইএফটি) করলে পাওয়া যাবে আমাদের অব্জার্ভড ইমেজ।
জেনে রাখা ভালো, ইউভি-কাভারেজের আইএফটি করলে পুরো অ্যারের বিম পাওয়া যায়, যার নাম সিন্থেসাইজড বিম। এর বিপরীতে একটা একক এন্টেনার বিমের নাম প্রাইমারি বিম। একটা আর্ট দিয়ে তোলা ছবির ফিল্ড অফ ভিউ (এফওভি) পাওয়া যায় তার একেকটা এন্টেনার প্রাইমারি বিমের মেইন লোবের ব্যাস থেকে, আর রেজলুশন পাওয়া যায় সিন্থেসাইজড বিমের মেইন লোবের ব্যাস থেকে। প্রাইমারি বিমের সাইজ নির্ভর করে একটা এন্টেনার ব্যাসের উপর ($\lambda/D$), আর সিন্থেসাইজড বিমের সাইজ নির্ভর করে সবচেয়ে লম্বা বেসলাইনের লেন্থের উপর ($\lambda/b$)। জিএমআরটি’র একটা এন্টেনার সাইজ ৪৫ মিটার হলে ২১ সেন্টিমিটার ওয়েভলেন্থে এফওভি হবে ১৬ আর্কমিনিট, মানে এই আর্টের তোলা ছবিতে আকাশের ১৬ আর্কমিনিট এলাকা একসাথে দেখা যাবে; মনে রাখতে হবে চাঁদের সাইজ প্রায় ৩০ আর্কমিনিট। আর এই আর্টের সবচেয়ে লম্বা বেসলাইন ২৫ কিমি হলে একই ওয়েভলেন্থে রেজলুশন হবে ১.৭ আর্কসেকেন্ড।
তার মানে আর্টের র ডেটা হচ্ছে কমপ্লেক্স ভিজিবিলিটি যার ইকুয়েশনের নাম রাইম। উপরের অব্জার্ভেশনের জন্য কয়টা ভিজিবিলিটি পাওয়া যাবে? ঐ ৪৩৫ টা বেসলাইনের প্রতিটা দিয়ে ১১ ঘণ্টার মধ্যে প্রতি ৩০০ সেকেন্ডে একটা করে ভিজিবিলিটি অব্জার্ভ করা হয়েছে, তাহলে মোট ভিজিবিলিটি হবে প্রায় ৫৭ হাজার। উপরের অব্জার্ভড এফএফটি প্যানেলের প্রতিটা ডটের কালার দিয়ে ঐ ইউ-ভি কোওর্ডিনেটের বেসলাইনে পাওয়া ভিজিবিলিটি দেখানো হয়েছে। এসব ভিজিবিলিটি থেকে প্রথমে ক্যালিব্রেশনের মাধ্যমে সব সিস্টেমেটিক ইফেক্ট দূর করতে হয়। তারপর সব ক্লিন ভিজিবিলিটি একটা গ্রিডের মধ্যে গড় করে আইএফটি করার মাধ্যমে চূড়ান্ত ইমেজ বানাতে হয়। ক্যালিব্রেশনের একটা বড় ধাপ হচ্ছে রাইম থেকে এন্টেনার প্রাইমারি বিম $\mathbf{B}(l,m)$ এর ইফেক্ট দূর করা। এর জন্য আমাদেরকে আগে একটা আর্টের বিভিন্ন এন্টেনার প্রাইমারি বিম বুঝতে হবে, যা আমরা শুরু করেছিলাম লাঞ্চের পরে।
১.৩। এন্টেনার প্রাইমারি বিম
লাঞ্চ ব্রেকের পর দুপুর আড়াইটা থেকে এন্টেনার প্রাইমারি বিম নিয়ে কথা শুরু হয় এবং আমাদেরকে ফোকাস করতে হয় লোফারের উপর। ওয়ার্কশপের মূল উদ্দেশ্য লোফারের একটা স্টেশনের বিম মডেল করা। এই আর্টের হাজার হাজার এন্টেনা ইউরোপ জুড়ে ছড়ানো।
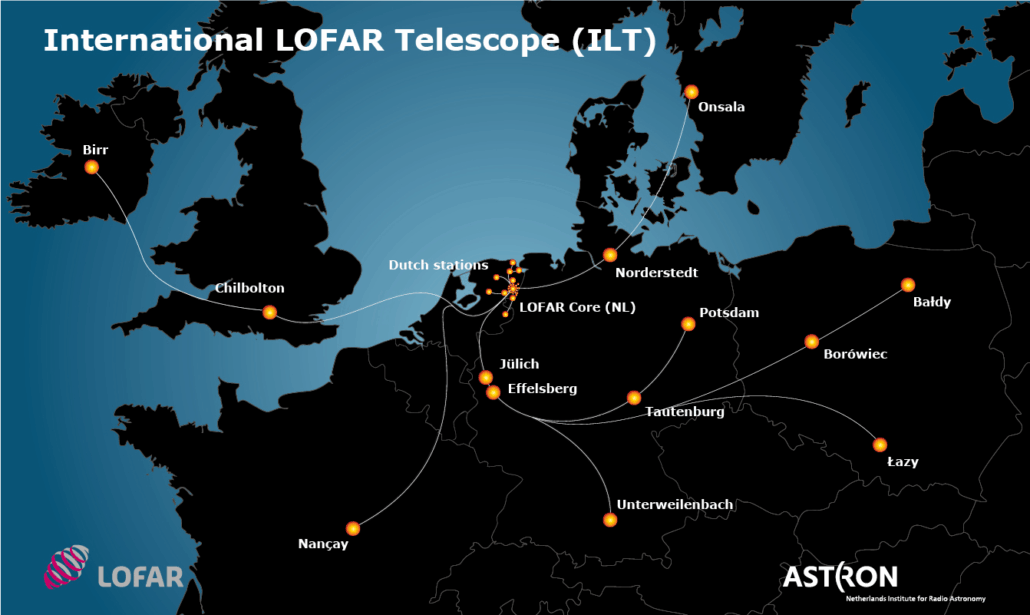
নেদারল্যান্ডে কোর থেকে চারটা স্পাইরাল আর্ম বের হয়ে প্রায় ৫০০ কিমি পর্যন্ত চলে গেছে। উত্তরে সুইডেনের ওনসালা থেকে দক্ষিণে ফ্রান্সের নান্সে ও জার্মানির উন্টারভাইলেনবাখ পর্যন্ত স্টেশন আছে, পশ্চিমে আয়ারল্যান্ডের বার থেকে পূর্বে পোল্যান্ডের বাউদি পর্যন্ত স্টেশন আছে। এই কারণে লোফারের সবচেয়ে লম্বা বেসলাইন প্রায় ১০০০ কিমি। হাই-ব্যান্ড এন্টেনাগুলো (এইচবিএ) ১১০ থেকে ২৪০ মেগাহার্জে অব্জার্ভ করে। নেদারল্যান্ডের ভিতরে লোফারের ৩০টা কোর স্টেশন আছে ৩.৫ কিমি’র মধ্যে, যার প্রতিটাতে দুইটা করে এইচবিএ স্টেশন আছে। একটা এইচবিএ কোর স্টেশনে মোট ৩৮৪টা এন্টেনা নিচের ফিগারের মতো করে সাজানো থাকে।

উপরের ছবিতে একটা এইচবিএ স্টেশনের কনফিগারেশন দেখানো হয়েছে। মোট ১৬টা ক্রস-ডাইপোল (ছবিতে নীল ক্রস) এন্টেনা নিয়ে একটা টাইল (লাল স্কয়ার) হয়, আর ২৪টা টাইল নিয়ে হয় একটা ৩০-মিটার স্টেশন (সবুজ সার্কেল)। একটা সিঙ্গেল ডাইপোলের বিমের সাইজ ১৫০ মেগাহার্জে প্রায় ৯০ ডিগ্রি (নীল সার্কেল), টাইলের বিম ২০ ডিগ্রি (লাল সার্কেল), আর স্টেশনের বিম মাত্র ৪ ডিগ্রি (সবুজ সার্কেল)। সেই পরিচিত $\lambda/D$ সূত্র মেনে এপার্চারের সাইজ যত বাড়ছে বিম তত ছোট হচ্ছে। লোফারের এমন একটা স্টেশন পুরো অ্যারের একটা এন্টেনা হিসেবে কাজ করে।
এই ব্যাপারটা নিয়ে আরো ভাবতে হবে। কাসা অফিসের পাশে আমাদের যে স্টার্ট আছে, তাতে ২৪টা এন্টেনা মিলে একটা অ্যারে তৈরি করছে, তবে প্রতিটা এন্টেনা খুব সিম্পল, তার ভিতরে একাধিক এলিমেন্ট নাই। কিন্তু লোফারের ৩০টা কোর স্টেশনে মোট ৬০টা এইচবিএ স্টেশনের প্রতিটা একটা সিঙ্গেল ডিশ এন্টেনার মতো কাজ করে, যাদের প্রত্যেকটা আবার ৩৮৪ এন্টেনার কালেকশন। এই কারণে লোফারের প্রাইমারি বিমও ৩৮৪ এন্টেনা একত্রিত করে বানাতে হয়।
এক্ষেত্রে তিনটা স্টেপ আছে যা উপরের ফিগারে (Brackenhoff et al. 2025) দেখানো হয়েছে। প্রথমে একটা ক্রস-ডাইপোলের ৯০ ডিগ্রি বিম (বাম থেকে ১ম প্যানেল) মডেল করা হয়, তারপর ১৬টা ডাইপোল বিম একসাথে করার জন্য বানানো হয় ২০ ডিগ্রি টাইল অ্যারে ফ্যাক্টর (২য় প্যানেল), এবং সবশেষে ২৪টা টাইল বিম একসাথে করার জন্য বানানো হয় ৪ ডিগ্রি স্টেশন অ্যারে ফ্যাক্টর (৩য় প্যানেল)। ডাইপোল বিমের সাথে টাইল ও স্টেশনের অ্যারে ফ্যাক্টর মিলালে পাওয়া যায় ৪ ডিগ্রি স্টেশন বিম, যা ৪র্থ ও শেষ প্যানেলে দেখা যাচ্ছে। একমাত্র ডাইপোল বিমটাই ইলেক্ট্রোম্যাগ্নেটিক (ইএম) সিমুলেশনের মাধ্যমে ফিজিকেলি মডেল করতে হয়; অ্যারে ফ্যাক্টরের জন্য জ্যামিতিই যথেষ্ট। লোফার একটা সফটওয়ার টেলিস্কোপ, একটা জিওমেট্রি মেশিন।
কিন্তু একটা ডাইপোলের বিম আসলে কি জিনিস। এটা বুঝতে সুবিধা হবে একটা এন্টেনাকে রিসিভার না ভেবে ট্রান্সমিটার হিসেবে চিন্তা করলে। একটা রেডিও এন্টেনা দিয়ে ট্রান্সমিট করার জন্য ফোকাল প্লেইনের ফিডে কারেন্ট পাঠাতে হবে, কারেন্ট মানে ইলেক্ট্রনের এক্সিলারেশন, আর আমরা জানি চার্জের ত্বরণ থাকলেই লাইট তৈরি হবে। ফিড থেকে তৈরি লাইট রিফ্লেক্টরে ধাক্কা খেয়ে আকাশে ছড়িয়ে যাবে। একটা এন্টেনার তৈরি লাইট যেদিকে যেভাবে ছড়িয়ে পড়ে তাকেই তার পাওয়ার প্যাটার্ন, রেডিয়েশন প্যাটার্ন বা বিম বলা হয়। টেলিস্কোপের ক্ষেত্রে একে ট্রান্সমিটিং বিম না ভেবে, রিসিভিং বিম ভাবতে হবে, কিন্তু দুইটা একই রকম।
এর নাম বিম, কারণ এন্টেনা একটা নির্দিষ্ট দিকে সবচেয়ে ভালো দেখে, এবং সেদিক থেকে দুই দিকে যত দূর যাওয়া যায় তার ভিশন তত খারাপ হয়। আমাদের চোখের উদাহরণ দিয়ে ব্যাপারটা পরিষ্কার করা যায়। আমরা যেকোনো কিছু পড়তে হলে আগে তা দুই চোখের মাঝখানে নিয়ে আসি, কারণ এফওভি’র ঠিক মাঝখানে আমাদের ভিশন সবচেয়ে ভালো। যেদিকে তাকাই সেদিকেই আমরা সবচেয়ে ভালো দেখি, তার থেকে দুই দিকে যত দূরে যাব ভিশন তত খারাপ হবে।

এই বিম প্যাটার্নের কারণ উপরের ফিগারে দেখানো হয়েছে। এখানে মেশ প্যাটার্নের ঠিক কেন্দ্রে একটা চার্জ আছে যার ত্বরণ $\mathbf{a}$ উপরের দিকে। চার্জের ত্বরণ যেদিকে হয় তার ঠিক পার্পেন্ডিকুলার দিকে রেডিয়েশন সবচেয়ে বেশি তৈরি হয়। পার্পেন্ডিকুলার থেকে যত প্যারালাল দিকে আসতে থাকব রেডিয়েশন তত কমবে। এক্সিলারেশন থেকে তৈরি এই রেডিয়েশনের ফ্লাক্স $S\propto \sin^2\theta$ যেখানে $\theta$ এক্সিলারেশন ভেক্টরের সাথে কোণ। এটাই সিমেট্রিক বিম প্যাটার্নের অন্তর্নিহিত উৎস।
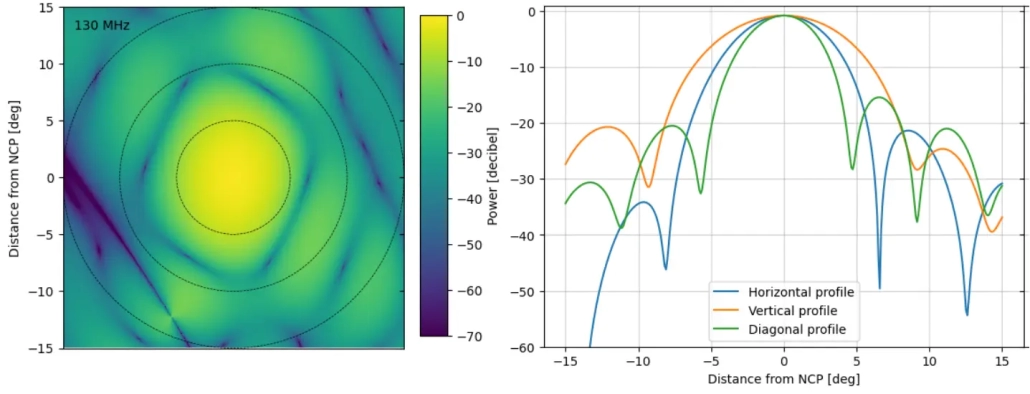
একটু উপরে লোফারের যে স্টেশন বিম দেখানো হয়েছে তার কেন্দ্রীয় ৩০ ডিগ্রি উপরে জুম করে দেখানো হচ্ছে। লোফারের স্টেশন বিম টাইম, ফ্রিকোয়েন্সি ও ডিরেকশনের সাথে পাল্টায়। এখানে নর্থ সেলেস্টিয়াল পোল (এনসিপি) বরাবর ১৩০ মেগাহার্জে বিম প্লট করা হয়েছে একটা নির্দিষ্ট সময়ে। বাম প্যানেলে আছে দ্বিমাত্রিক বিম, আর ডান প্যানেলে তার কিছু একমাত্রিক প্রফাইল। সব দেয়া হয়েছে ডেসিবেল (একটা কোয়ান্টিটির ১০-ভিত্তিক লগারিদমের ২০ গুণ) ইউনিটে কারণ এটা বিমের পাওয়ার মাপার স্ট্যান্ডার্ড ইউনিট। বিমের মান ০ থেকে ১ এর মধ্যে একটা নাম্বার, ১ মানে এন্টেনার সেন্সিটিভিটি সেদিকে সবচেয়ে বেশি, ০ মানে একদম খারাপ। উপরের ফিগারে ০ ডেসিবেল মানে ১, -২০ ডেসিবেল মানে তার চেয়ে ১০০ গুণ কম, -৩০ ডেসিবেল মানে ১০০০ গুণ কম, আর -৬০ ডেসিবেল মানে ১ মিলিয়ন গুণ কম। ডানের প্রফাইলে মেইন লোবের ব্যাস পরিষ্কার বুঝা যাচ্ছে, যা লোফারের একটা স্টেশনের এফওভি।
ওয়ার্কশপে স্টুডেন্টদের একটা প্রশ্ন ছিল এই প্রাইমারি বিম জেনে আমাদের কি লাভ। উত্তর পাওয়া যাবে রাইমের মধ্যে। রাইমে যে $\mathbf{B}(l,m)$ ছিল সেটাই বিম। রাইম আমাদেরকে কমপ্লেক্স ভিজিবিলিটি দেয়, কিন্তু তা থেকে যদি আকাশের আসল ইন্টেন্সিটি ডিস্ট্রিবিউশন $\mathbf{E}(l,m)$ বের করতে চাই তাহলে $\mathbf{V}(u,v)$ কে আইএফটি করতে হবে। কিন্তু আইএফটি করা সম্ভব না যদি ইন্টিগ্রালের ভিতরে $\mathbf{B}$ থাকে। আকাশের ইমেজের উপর বিমের ইফেক্ট বুঝার জন্য ধরে নিতে হবে, আমাদের অব্জার্ভড ইমেজ হচ্ছে আকাশের ট্রু ইমেজের সাথে প্রাইমারি বিমের মাল্টিপ্লিকেশনের ফল। সুতরাং আকাশের যে অব্জেক্ট ফিল্ডের ঠিক কেন্দ্রে থাকবে তার ইন্টেন্সিটি পাল্টাবে না, কারণ সেখানে বিমের মান ১। কিন্তু ফিল্ডের সেন্টার থেকে যত দূরে যাব, বিমের মান তত শূন্যের দিকে যাবে, এবং অব্জেক্টের ইন্টেন্সিটি গুণের কারণে ততই কমতে থাকবে। একটা ওয়াইড-ফিল্ড ইমেজে সব অব্জেক্টের, বা সব পিক্সেলের আসল মান যদি আমরা ফিরে পেতে চাই তাহলে পুরো ইমেজকে প্রাইমারি বিম দিয়ে ভাগ করতে হবে। বিমই যদি না জানি, ভাগ করব কিভাবে।
ওয়ার্কশপে আমরা শুধু লোফারের বিম মডেলিং নিয়ে কাজ করেছি, সেটা কোনো ইমেজ থেকে বাদ দেয়ার ঝামেলায় যাইনি। কারণ তার জন্য অনেক জটিল হিসাব-নিকাশ দরকার। প্রথমত আমাদের র অব্জার্ভেশন থাকে ফুরিয়ে প্লেইনে। রিয়েল প্লেইনে বিম যদি ইমেজের সাথে গুণ হয়, তাহলে ফুরিয়ে প্লেইনে বিমের সাথে ভিজিবিলিটির হচ্ছে কনভলুশন। বিম বাদ দেয়ার জন্য তাই ফুরিয়ে প্লেইনে ভাগ করা যায় না, করতে হয় ডিকনভলুশন, যা অনেক জটিল। ডিকনভলুশনের মাধ্যমে বিমের ইফেক্ট দূর করার পর ভিজিবিলিটিকে আইএফটি করলে ক্লিন ইমেজ পাওয়া যায়।
১.৪। টিমেয়াস
একটা টি-ব্রেকের পর আট গ্রুপ যার যার প্রজেক্ট শুরু করে। প্রথম দিনের টাস্ক ছিল কাসা’র এইচপিসি সার্ভার টিমেয়াসে টানেলিং করে একটা জুপিটার নোটবুকের মাধ্যমে লোফারের হামাকার বিম প্লট করা; ডাচ বিজ্ঞানী জে পি হামাকার ইএম সিমুলেশনের মাধ্যমে বিমের এই মডেল বানিয়েছিলেন, পার্ফেক্ট না হলেও এটাই এখন পর্যন্ত জানা লোফারের সবচেয়ে ভালো বিম মডেল। এটা প্লট করার জন্য আগে একটা মেজারমেন্ট সেট (এমএস) সিমুলেট করতে হয়। এস্ট্রোনমিতে রিয়েল ইমেজ যেমন .FITS ফাইল হিসেবে রাখা হয়, তেমনি কমপ্লেক্স ভিজিবিলিটি রাখা হয় .MS ফাইল হিসেবে। এমএস ফাইল সিমুলেট করার জন্য synthms এবং হামাকার বিম প্লট করার জন্য everybeam টিমেয়াসে আগে থেকেই আমরা ইন্সটল করে রেখেছি, স্টুডেন্টদের কাজ টিমেয়াসের জুপিটার নোটবুকে এগুলো ইউজ করা।
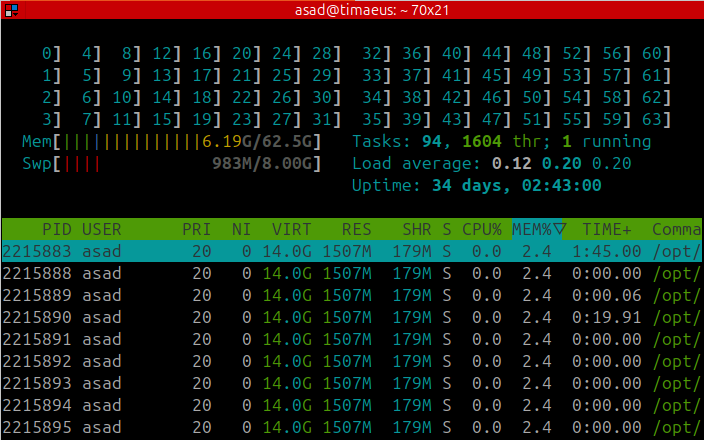
সার্ভারে লগিন করার জন্য সবার একটা কমন একাউন্ট করে রেখেছিলাম, ssh দিয়ে সবাই সেই একাউন্টে লগিন করে যার যার গ্রুপের ফোল্ডারে যেতে পেরেছে। আট গ্রুপের জন্য আটটা ওয়ার্কিং ফোল্ডার বানানোর পাশাপাশি আমরা ৮টা screen খুলে রেখেছিলাম। প্রত্যেক স্ক্রিন একটা ইউনিক পোর্টে জুপিটার ল্যাব রান করছিল। প্রত্যেক গ্রুপকে যার যার স্ক্রিনে টানেল করতে হয়েছে ssh -N -f -L ইউজ করে, টানেলিঙের পরই প্রত্যেক গ্রুপ নিজেদের ল্যাপটপে যার যার জুপিটার নোটবুক ওপেন করতে পেরেছে। সার্ভারের লাইভ তথ্য প্রজেক্টরের স্ক্রিনে দেখা যাচ্ছিল উপরের ফিগারের মতো। আমাদের ৬৪টা সিপিইউ থ্রেড আর ৬৪ গিগা র্যামের কতটা ইউজ হচ্ছে তার ট্র্যাক রাখতে বলছিলাম সবাইকে এই htop আউটপুটের মাধ্যমে।
প্রায় সব গ্রুপই ভালোভাবে শুরু করতে পেরেছিল, কিন্তু ডিজাস্টার হয়েছিল আমাদের দিক থেকে। আগে থেকে শেয়ার করা কোডে কিছু সমস্যা থাকার কারণে অনেক ফ্রিকোয়েন্সির জন্য অনেক এমএস ফাইল তৈরি হয়ে যাচ্ছিল, আর সবাই যদি সব ফ্রিকোয়েন্সির বিম আলাদা আলাদাভাবে বানাতে থাকে তাহলে যে শীঘ্রই সার্ভারের এলোকেট করা স্পেস শেষ হয়ে যাবে তা আগে ভাবিনি। প্রথম দিন শেষ হয় ৬০ গিগা র্যাম ইউসেজের মাধ্যমে, এবং আমরা জানি ৬৪ গিগা র্যামের একটা সার্ভারে ইউসেজ ৬০ গিগা অতিক্রম করলে সেই সার্ভারে আর কিছুই ঠিকঠাক করা সম্ভব না। আমরা তাই প্রথম দিন শেষ করি পরের দিন আরো ভালো সার্ভার ম্যানেজমেন্টের স্বপ্ন দেখিয়ে।
২। দ্বিতীয় দিন
দ্বিতীয় দিন সকাল সাড়ে নয়টায় (পুরো আধা ঘণ্টা দেরিতে) আমি গ্রুপ প্রজেক্টের আসল প্ল্যানটা সবার সাথে শেয়ার করি। তার আগে রাত জেগে সার্ভারে স্পেস ও মেমোরির সব সমস্যা সমাধান করেছিলাম টিএ-দের সাথে কথা বলে। আমরা সব ফ্রিকোয়েন্সির জন্য একটা কমন বিম ফাইল ক্রিয়েট করে রেখেছিলাম নাম্পাই অ্যারে হিসাবে, যাতে কোনো গ্রুপ নতুন করে ফাইল ক্রিয়েট না করে। সকালে সবাইকে সার্ভার ইউজ করার এটিকেটও কিছুটা শিখাতে হয়েছে। ফল খুব ভালো ছিল। দ্বিতীয় দিন সার্ভার নিয়ে কোনো সমস্যা হয়নি।
২.১। লোহেইজ: লোফারের হামাকার-জের্নিকে বিম
দিনটা শুরু করেছিলাম একটা লেকচার দিয়ে, যার বিষয় ছিল প্রজেক্টের প্ল্যান: জের্নিকে পলিনমিয়াল দিয়ে লোফারের হামাকার বিম মডেল করা। এটা লোফারের হামাকার-জের্নিকে বিম হবে বলে নাম দিয়েছিলাম লোহেইজ। এই প্রসঙ্গে একটু ইতিহাসও চলে এসেছিল। ফ্রিটস জের্নিকে ১৯২০-এর দশকে নেদারল্যান্ডের খ্রোনিঙেনে ইয়াকোবুস কাপ্টাইনের (যিনি প্রথম সূর্য থেকে মিল্কিওয়ের কেন্দ্রের দূরত্ব মেপেছিলেন) এসিস্টেন্ট হিসেবে কাজ শুরু করেছিলেন, পরে ফেইজ-কন্ট্রাস্ট মাইক্রোস্কোপ ইনভেন্ট করার জন্য ফিজিক্সে নোবেল প্রাইজ পান। এই মাইক্রোস্কোপের এবারেশন মডেল করার জন্যই তিনি জের্নিকে পলিনমিয়াল আবিষ্কার করেছিলেন।
আমি ইউনিভার্সিটি অফ খ্রোনিঙেনের কাপ্টাইন এস্ট্রোনমিকেল ইনস্টিটিউটে পিএইচডি করেছিলাম লোফার নিয়ে ২০১২ থেকে ২০১৬ সালে। আমাদের সায়েন্স ক্যাম্পাসের নামই ছিল জের্নিকে ক্যাম্পাস। তারপর ২০১৬’র শেষে পোস্টডকের জন্য যখন সাউথ আফ্রিকার কেইপ টাউনে মুভ করি, তখন জের্নিকে পলিনমিয়াল ইউজ করেছিলাম মিয়ারক্যাটের প্রাইমারি বিম মডেল করার জন্য। পোস্টডকের সময় আমার লেখা পাইথন প্যাকেজটাই এই ওয়ার্কশপের স্টুডেন্টরা ইউজ করেছে, তবে এবার মিয়ারক্যাটের জন্য না, লোফারের প্রাইমারি বিম মডেলিঙের জন্য।
জের্নিকে পলিনমিয়াল একটা সিকোয়েন্স যার প্রত্যেকট পলিনমিয়াল ইউনিট ডিস্কে অর্থোগনাল। সিকোয়েন্সের প্রতিটা পলিনমিয়াল চিহ্নিত করা হয় রেডিয়াল অর্ডার $n$ ও এঙ্গুলার ফ্রিকোয়েন্সি $m$ দিয়ে; পজিটিভ ফ্রিকোয়েন্সি কোসাইন ফেইজ, আর নেগেটিভ সাইন ফেইজ। উপরে প্রথম ১০ অর্ডার ও ফ্রিকোয়েন্সির জের্নিকে পলিনমিয়ালের ছবি দেয়া হয়েছে। পোলার কোর্ডিনেট $\rho,\phi$ দিয়ে সার্বিক ইকুয়েশনটা এভাবে লেখা যায়:
$$ Z_n^{m}(\rho,\phi) = R_n^{|m|}(\rho) [\delta_{m\ge 0} \cos(m\phi) + \delta_{m\lt 0} \sin(|m|\phi) ] $$
যেখানে $\delta_{m\lt 0}$ একটা ডেল্টা ফাংশন যার মান শুধু নেগেটিভ ফ্রিকোয়েন্সির জন্য ১, বাকি সব ক্ষেত্রে শূন্য, আর $R_n^{|m|}$ একটা রেডিয়াল ফাংশন যা শুধু রেডিয়াস, অর্ডার ও ফ্রিকোয়েন্সির উপর নির্ভর করে। জের্নিকে এই ফাংশন বানিয়েছিলেন মাইক্রোস্কোপের এপার্চার মডেল করার জন্য, এবং এস্ট্রোনমিতেও এপার্চার মডেলিঙের জন্য এটা ইউজ করা হয়। আগেই বলেছি, টেলিস্কোপের প্লেইন আর আকাশের প্লেইন একে অপরের ফুরিয়ে ট্রান্সফর্ম, মানে এপার্চার প্লেইন (ডিশ মিরর বা এন্টেনার সার্ফেস) আর প্রাইমারি বিম (বিভিন্ন দিকে সেন্সিটিভিটি) একে অপরের ফুরিয়ে ট্রান্সফর্ম। বিম এপার্চারের ফুরিয়ে ট্রান্সফর্ম হলেও লোফারের ক্ষেত্রে এপার্চারের বদলে বিমটাই জের্নিকে দিয়ে মডেল করা যৌক্তিক হবে। কারণ লোফারের এপার্চার সার্কুলার না, অনেকটা রেক্টেঙ্গুলার, কিন্তু বিম কিছুটা হলেও সার্কুলার যা জের্নিকের সার্কুলার সিমেট্রির সাথে মিলে।
স্টুডেন্টদের কাজ ছিল আমাদের তৈরি করা হামাকার বিম $B_H(l,m)$ প্রথমে জের্নিকে পলিনমিয়াল দিয়ে ডিকম্পোজ করা, ডিকম্পোজিশন থেকে পাওয়া সব জের্নিকে কোএফিশেন্ট সর্ট করে সেখান থেকে সবচেয়ে ভালোগুলো সিলেক্ট করা, এবং সবচেয়ে ভালো সব কোএফিশেন্ট দিয়ে একটা বিম মডেল $B_Z(l,m)$ তৈরি করা। পুরো কাজটাই তারা করেছে বিম জোন্স মেট্রিক্সের শুধু প্রথম কম্পোনেন্টের ($xx$) জন্য। ডিকম্পোজিশনের জন্য হামাকার বিমের সাথে জের্নিকে পলিনমিয়ালের সুডো-ইনভার্স গুণ করতে হয়েছে, যার ফলে পাওয়া গেছে জের্নিকে কোএফিশেন্ট
$$ C = (Z^TZ)^+ Z^T B_H $$
যেখানে $^+$ মুর-পেনরোজ সুডো-ইনভার্স এবং $^T$ ট্রান্সপোজ। কয়টা জের্নিকে মোড দিয়ে ডিকম্পোজ করা হবে তা গ্রুপের স্টুডেন্টদের উপর ছেড়ে দিয়েছিলাম। যেমন, ২০০ মোড দিয়ে ডিকম্পোজ করলে ২০০টা কোএফিশেন্ট পাওয়া যাবে। পরের কাজ এখান থেকে সবচেয়ে ভালো ৩০/৪০ টা কোএফিশেন্ট সিলেক্ট করা। কিভাবে এবং কয়টা কোএফিশেন্ট সিলেক্ট করা উচিত সেই সিদ্ধান্তও স্টুডেন্টদের উপর ছেড়ে দেয়া হয়েছিল। সিলেকশনের পর হামাকার-জের্নিকে বিম লোহেইজ রিকনস্ট্রাক্ট করা হয় এভাবে:
$$ B_Z = \sum_{i\in L} C_i Z_i $$
যেখানে $L$ হচ্ছে সিলেক্ট করা জের্নিকে মোডগুলোর নোল ইন্ডেক্সের ($l$) লিস্ট। অর্ডার ও ফ্রিকোয়েন্সি ইউজ করে সব জের্নিকে পলিনমিয়ালের জন্য সিকোয়েনশিয়াল ইন্ডেক্স তৈরি করা যায় ১ থেকে শুরু করে, যার নাম নোল ইন্ডেক্স। এতে হিসাব অনেক সহজ হয়; আগে যেখানে প্রত্যেক পলিনমিয়াল আইডেন্টিফাই করতে দুইটা নাম্বার (অর্ডার ও ফ্রিকোয়েন্সি) লাগত, এখন কেবল একটা লাগছে।
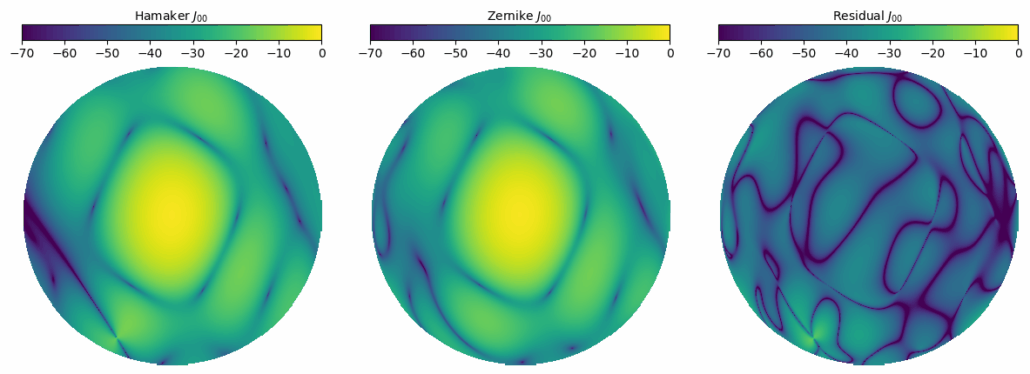
উপরের ছবিতে প্রথম প্যানেলে আছে অরিজিনাল হামাকার বিম $B_H$ (১৫ ডিগ্রি পর্যন্ত), মাঝের প্যানেলে রিকন্সট্রাকশনের পর পাওয়া লোহেইজ বিম $B_Z$, এবং শেষ প্যানেলে এই দুয়ের ডিফারেন্স দেখানো হয়েছে রেসিডুয়াল $R=B_H-B_Z$ হিসাবে। কালারবারে ডেসিবেলে পাওয়ার দেয়া আছে। রেসিডুয়াল শূন্যের যত কাছাকাছি হবে, লোহেইজ মডেল তত ভালো ধরে নিতে হবে। দুইশটা মোড থেকে সবচেয়ে ভালো ৪০টা নিয়ে যে রেসিডুয়াল পাওয়া গেল তার মান প্রায় সবখানে -৩০ থেকে -৫০ ডেসিবেল, যা খারাপ না।
এখানে স্টুডেন্টরা আরেকটা ব্যাপার নিয়ে এক্সপেরিমেন্ট করতে পেরেছে। আরো উপরে লোফার বিমের যে ছবি ও একমাত্রিক প্রফাইল দিয়েছি সেখানে ৩০ ডিগ্রি এরিয়া দেখানো হয়েছিল। এত বড় এঙ্গুলার এরিয়াতে মেইন লোবের পাশাপাশি দুইটা সাইডলোব চলে আসে, তাই মডেল করতে আরো হায়ার অর্ডার পলিনমিয়াল লাগে। কিন্তু টিমেয়াসের লোড কমানোর জন্য স্টুডেন্টরা বিম মডেল করেছে সর্বোচ্চ ১৫ ডিগ্রি পর্যন্ত, তবে কোনো গ্রুপ চাইলে এটা নিয়ে আরো এক্সপেরিমেন্ট করতে পারত, মানে আরো ছোট অংশ মডেল করতে কোন পলিনমিয়াল বেশি লাগছে তা বের করতে পারত।
স্টুডেন্টদের শেষ কাজ ছিল উপরের ডিকম্পোজিশন ও রিকনস্ট্রাকশন, অর্থাৎ স্পার্স রিপ্রেজেন্টেশনের কাজটা ১১০ থেকে ১৭০ মেগাহার্জের মধ্যে অনেক ফ্রিকোয়েন্সির জন্য করা। স্পার্স রিপ্রেজেন্টেশন আমাদের জন্য খুব দরকারি কারণ ভিজিবিলিটি থেকে বিমের ইফেক্ট বাদ দিতে হলে অনেক কম্পিউটেশন লাগে, বিম যত কম প্যারামিটার দিয়ে বর্ণনা করা যায় কম্পিউটেশন তত এফিশেন্ট হয়। একটা ১৫ ডিগ্রি বিমের ডাইমেনশন যদি এক এক্সিসে ৩০০ হয়, তাহলে তাতে মোট পিক্সেল থাকবে ৯০ হাজার; কিন্তু মাত্র ৪০টা জের্নিকে কোএফিশেন্ট দিয়ে আমরা ৯০ হাজার পিক্সেলের মান পুনরুদ্ধার করে ফেলতে পারছি।
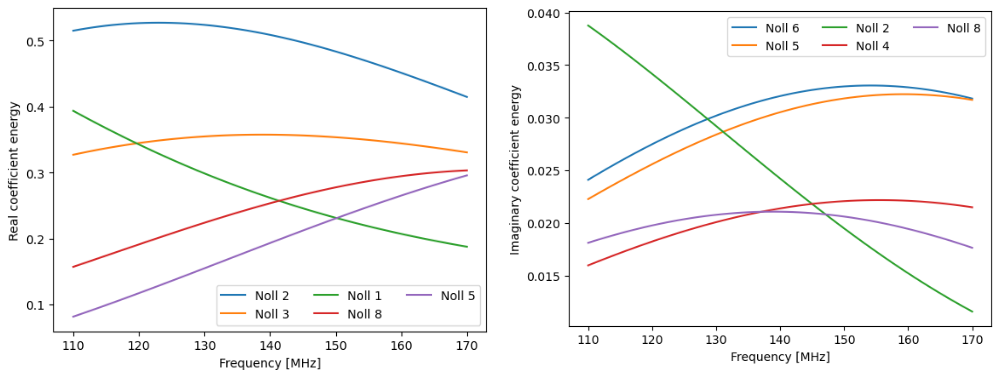
আবার ১১০ থেকে ১৭০ মেগাহার্জে যদি ৬০টা ফ্রিকোয়েন্সি চ্যানেলে বিম বের করতে হয় তাহলে মোট ভ্যালু লাগত ৯০,০০০ × ৬০ = ৫৪ লাখ। কিন্তু জের্নিকে কোএফিশেন্ট প্রত্যেক ফ্রিকোয়েন্সির জন্য আলাদা আলাদাভাবে স্টোর করতে হলেও মোট ৪০ × ৬০ = ২৪০০ ভ্যালু লাগবে। উপরের ছবিতে ১৫ ডিগ্রি হামাকার বিম মডেলিঙের জন্য সবচেয়ে স্ট্রং ৫টা জের্নিকে কোএফিশেন্টের মান প্লট করা হয়েছে ফ্রিকোয়েন্সির সাপেক্ষে। প্রত্যেকটার নোল ইন্ডেক্স লেজেন্ডে দেয়া আছে। বাম প্যানেলে রিয়েল ও ডান প্যানেলে ইমাজিনারি পার্টের কোএফিশেন্ট আছে। ফ্রিকোয়েন্সির সাপেক্ষে কোএফিশেন্টের পরিবর্তন খুব স্মুথ, যা ৩০ ডিগ্রি মডেলের ক্ষেত্রে দেখা যায়নি। প্রত্যেক ফ্রিকোয়েন্সির জন্য রেসিডুয়াল বের করে একতা মডেলিং এরর বের করতে হয়েছিল প্রত্যেক গ্রুপকে, এবং দেখতে হয়েছিল এই এরর ফ্রিকোয়েন্সির সাথে কিভাবে পাল্টায়।
২.২। গ্রুপ প্রজেক্ট
কাসা অফিসের পরিবেশে প্রত্যেক গ্রুপ বেশ প্রডাক্টিভ ছিল। পরিবেশে আরো একাডেমিক আবহ আনার জন্য আমি টিমেয়াস নামের রহস্যও পরিষ্কার করেছিলাম, ‘টিমেয়াস’ প্লেটোর একটা ডায়লগের নাম। প্লেটো রচনাসমগ্র কাসা লাইব্রেরিতে রাখা ছিল। বইটা দেখিয়ে বললাম কেউ চাইলে ‘টিমেয়াস’ এক দুই পাতা পড়ে দেখতে পারে। আদৌ কেউ পড়েছে কি না জানি না, কিন্তু অনেককেই বইটা উল্টে পাল্টে দেখতে দেখেছি। বই পড়ার কারো সময় থাকার কথা না। উপরের সব কনসেপ্ট এক দিনের মধ্যে বুঝে আর এক দিনে পুরো একটা প্রজেক্ট শেষ করে আবার প্রেজেন্ট করা, শুনতে অনেক কাজ মনে হতে পারে। কিন্তু এতটা ব্যস্ততা না থাকলে ওয়ার্কশপ জমে না, গ্রুপ মেম্বারদের মধ্যে বন্ডিংও হয় না। নিচের ছবিগুলো দেখলে মনে হবে বন্ডিং আসলেই হয়েছিল।
এক স্টুডেন্ট বলল এই ওয়ার্কশপের সবচেয়ে ভালো দিক ছিল কোনো প্রেসার ছাড়া অনেক কাজ করতে পারা। ওয়ার্কশপে আমরা এমন একটা পরিবেশই তৈরি করতে চাই। অনেক কাজ থাকবে, যে যতটুক পারে করবে, এবং একেক জন ওয়ার্কশপ থেকে একেক ধরনের শিক্ষা নেবে; এখানে ‘শিক্ষা’ শব্দটা ভালো খারাপ দুই অর্থেই ইউজ করছি। ফাইনাল প্রেজেন্টেশনের পর আমি সবাইকে ওয়ার্কশপ থেকে তাদের আসল টেইকঅ্যাওয়ে জিজ্ঞাসা করেছিলেম এবং সবার উত্তর শুনে বুঝতে পেরেছি এই ধরনের ওয়ার্কশপের একটা বড় চাহিদা ঢাকায় আসলেই আছে।
সবচেয়ে ভালো এক বা একাধিক গ্রুপকে প্রাইজ দেয়ার কথা ওয়ার্কশপের আগে বলেছিলাম, কিন্তু সবার প্রেজেন্টেশন শুনে সেরকম নির্দিষ্ট কোনো গ্রুপ সিলেক্ট করতে আর ইচ্ছা করেনি, তবে ভবিষ্যতে আরো রিগোরাস ইভালুয়েশন রাখার ইচ্ছা আছে।
উপরের স্লাইডশো’র শেষে সব গ্রুপের প্রেজেন্টেশনের ছবি আছে। কে কি বলেছিল আমার খুব বেশি মনে নাই, কিন্তু প্রত্যেক গ্রুপ নিয়ে কিছু লেখার চেষ্টা করছি স্লাইডশো’র ছবি দেখে। গ্রুপ ১ থিওরিতে বেশ আগ্রহ দেখিয়েছে, রিগোরাস ফ্লোচার্ট থেকে বুঝা যায় সিস্টেমেটিক এনালাইসিসের প্রতি আগ্রহ অনেক। গ্রুপ ২ অনেক কাজ করেছে ঠিক কতগুলো কোএফিশেন্ট রাখা উচিত সেই থ্রেশল্ড বের করার জন্য। গ্রুপ ৩ হায়ার ফ্রিকোয়েন্সিতে বেশি মডেলিং এরর পাওয়ার কারণ নিয়ে বেশ ভেবেছে। গ্রুপ ৪ ফ্রিকোয়েন্সির সাথে এরর প্রথমে কমা ও পরে বাড়ার ভালো প্লট বানিয়েছে। গ্রুপ ৫ কয়টা কোএফিশেন্ট রাখা উচিত সেই থ্রেশল্ড নিয়ে বেশ অরিজিনাল উপায়ে চিন্তা করেছে। গ্রুপ ৬ থিওরি আর কম্পিউটেশন দুই সেকশনেই বেশ ডিটেল প্রেজেন্টেশন বানিয়েছে। গ্রুপ ৭ থ্রেশল্ড এবং ফ্রিকোয়েন্সির সাথে এরর, দুই দিকেই অনেক চিন্তা করে সবচেয়ে বেশি সংখ্যক প্লট বানিয়েছে। গ্রুপ ৮ ছিল সবচেয়ে ছোট ও ফ্রেশ, তাদের রেজাল্ট খুব ভালো না হলেও থিংকিং নিঃসন্দেহে ছিল অরিজিনাল। তাই কোনো গ্রুপকেই আর আলাদা করে প্রাইজ দেইনি। সবাই ভালো।
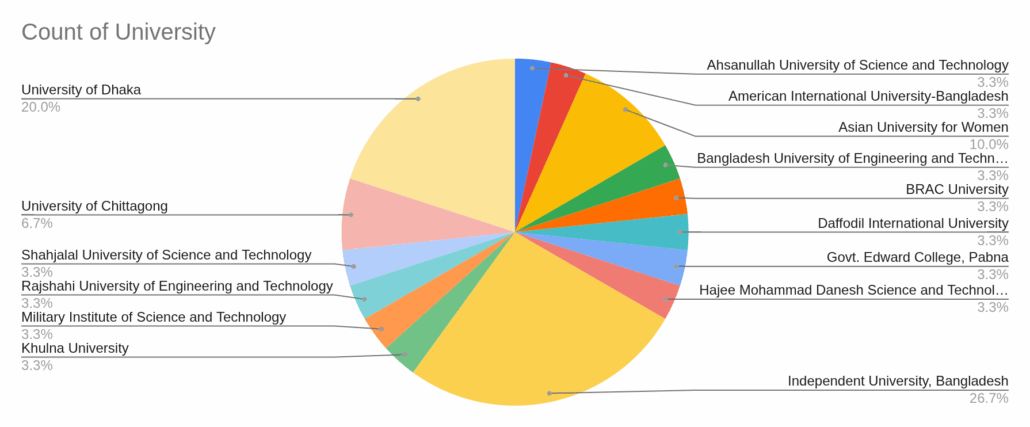
মোট ১৫টা ইউনিভার্সিটি থেকে স্টুডেন্টরা এসেছিল, কয়েক জনের অবশ্য পড়াশোনা শেষ, সুতরাং তারা অফিসিয়ালি এখন কোনো ইউনিভার্সিটিতে নেই, তবু তাদের আলমা মাটার নিয়েছি। সব স্টুডেন্ট ও টিএ’র লিস্ট এখানে পাওয়া যাবে। সবচেয়ে বেশি আইইউবি থেকে কারণ আইইউবি থেকে এপ্লিকেশনও সবচেয়ে বেশি ছিল, যেহেতু আইইউবির স্টুডেন্টদের পক্ষে এসব ওয়ার্কশপে যোগ দেয়া লজিস্টিক দিক থেকে সবচেয়ে সহজ। এর পর সবচেয়ে বেশি স্টুডেন্ট এসেছে ঢাকা বিশ্ববিদ্যালয় থেকে। তার পরে চট্টগ্রাম বিশ্ববিদ্যালয় এবং এশিয়ান ইউনিভার্সিটি ফর উইমেন। এছাড়া সাস্ট, রুয়েট, এমআইএসটি, খুলনা ইউনি, আহসানুল্লাহ, এআইইউবি, বুয়েট, ব্র্যাক ইউনি, ড্যাফোডিল, এডওয়ার্ড কলেজ, এবং হাজী দানেশ থেকে ১ জন করে এসেছিল।
এশিয়ান ইউনি থেকে দুই জন আফগান স্টুডেন্ট এসেছিল বলেই আমাদের পুরো ওয়ার্কশপ ইংলিশে করতে হয়েছে, যা ছিল সবার জন্যই অসাধারণ অভিজ্ঞতা। কাসা বাংলাদেশে অবস্থিত, কিন্তু কাসা একটা ইউনিভার্সিটির, আর বিশ্ববিদ্যালয় মানেই সেখানে বিশ্বের বিভিন্ন প্রান্ত থেকে স্টুডেন্ট আসতে হবে। যত দিন যাবে কাসার আন্তর্জাতিক পরিসর তত বাড়বে। কাসা বাংলাদেশের, কিন্তু শুধু বাংলাদেশীদের নয়, একইসাথে বাংলাদেশে পড়তে থাকতে বা কাজ করতে আসা সব মানুষের, তা তার দেশ জাতি ধর্ম জেন্ডার স্বভাব যাই হোক না কেন।

ওয়ার্কশপের পর প্রত্যেককে একটা সার্টিফিকেট পাঠানো হয়েছে ইমেইলে। সার্টিফিকেটের একটা উদাহরণ উপরে দেয়া হয়েছে। দেখা যাচ্ছে ওয়ার্কশপের পোস্টারের মতোই সার্টিফিকেটের ব্যাকগ্রাউন্ডে আছে মিকেলাঞ্জেলো আন্তোনিওনি’র সিনেমা ‘রেড ডেজার্ট’ (১৯৬৪) থেকে একটা দৃশ্য, যেখানে ইতালির বোলোনিয়া শহরের কাছে মেদিচিনা রেডিও অব্জার্ভেটরি দেখা যাচ্ছে। জেমস বন্ড থেকে শুরু করে অনেক সিনেমাতেই রেডিও দুরবিন ব্যবহার করা হয়েছে, কিন্তু আন্তোনিওনির ইউজের সাথে অন্য কারো ইউজ মেলানো যাবে না। ‘রেড ডেজার্ট’ আধুনিক ইন্ডাস্ট্রিয়াল পৃথিবীতে মানুষের এলিয়েনেশনের সবচেয়ে অদ্ভুত চিত্রায়ন; এই এলিয়েনেশন বুঝানোর জন্য তিনি ইউজ করেছেন বোলোনিয়ার আর্ট। ছবির দৃশ্যের একটু পরেই মনিকা ভিত্তি’র চরিত্র এক শ্রমিকের কাছে জানতে চায়, এটা কি বানানো হচ্ছে? শ্রমিক উত্তর দেয়, এর মাধ্যমে মহাবিশ্বের কথা ‘শোনা’ যাবে। সিনেমাটা যারা দেখবেন তারা এই উত্তরের মুহূর্তে একটা একজিস্টেনশাল ধাক্কা খাবেনই।
এই আর্টিকেলের চ্যাটজিপিটি দিয়ে করা ইংলিশ অনুবাদ পাওয়া যাবে এখানে: CASSA Workshop 1: Unclouding the thousand eyes of an Array Radio Telescope.
রেফারেন্স
- Asad et. al., 2021, ‘Primary beam effects of radio astronomy antennas,’ MNRAS, 502, 2970-2983.
- Burke et al., 2019, An Introduction to Radio Astronomy, Cambridge UP.
- Condon & Ransom, 2016, Essential Radio Astronomy, Princeton UP.
- Hamaker, 1996, ‘Understanding radio polarimetry,’ A&A Supplement Series, 117, 137-147.
- Smirnov, 2011, ‘Revisiting the radio interferometer measurement equation,’ A&A, 527, A106.
- Thompson et al., 2017, ‘Interferometry and Synthesis in Radio Astronomy,’ Springer Open.
- van Haarlem et al., 2013, ‘LOFAR: The LOw-Frequency ARray,’ A&A, 556, A2.