A field is called a vector field if it has both a magnitude and a direction to describe each point. Means a vector has to be considered at each point of this field. The field can be of any dimension, but vector fields in our universe are essentially three-dimensional. But we can best visualize two-dimensional vector fields. Just as the three dimensions of space are reduced to two dimensions in Einstein’s curveball, reducing the three dimensions of the electromagnetic field to two is much easier to think about.

A scalar field $f$ can be transformed into a vector field ($\mathbf{F}$) by gradients (Nabla or Del: $\nabla$), whose mathematical form is shown below using Cartesian coordinates in three-dimensional Euclidean space.

$$\mathbf{F} = \nabla f = \frac{\partial f}{\partial x} \hat{i} + \frac{\partial f}{\partial y} \hat{j} + \frac {\partial f}{\partial z} \hat{k}$$

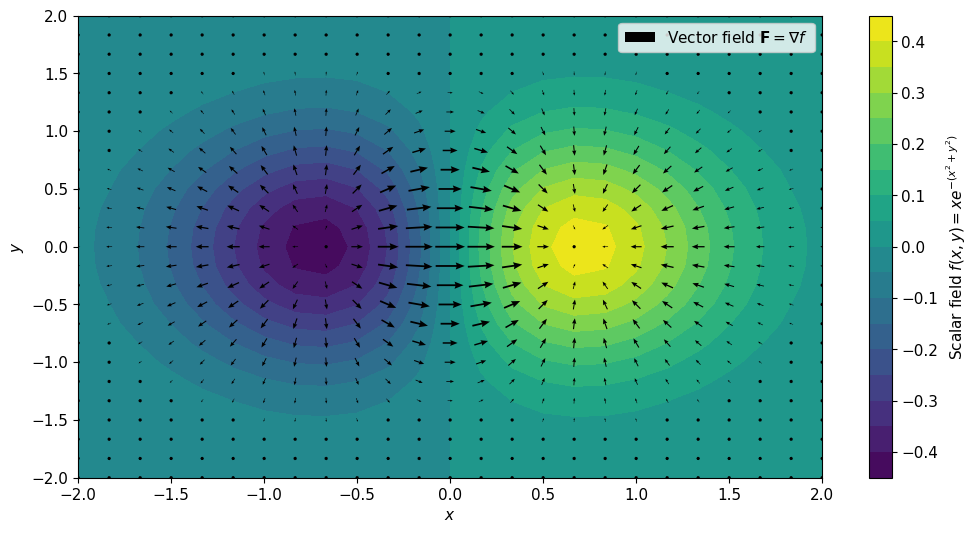
where $\hat{i},\hat{j},\hat{k}$ are unit vectors of $x,y,z$ ordinates, respectively. A two-dimensional visualization of this is shown below.

A scalar function $f(x,y)=xe^{-(x^2+y^2)}$ is shown using color above, with the colorbar on the right. The gradient of this function $\nabla f$ is shown by arrows, where the length of the arrow is the value of the vector at a given point.

Divergence indicates the amount of source (outward vector) or sink (inward vector) somewhere inside a vector field. Divergence positive at a point in the field means that the magnitude of the vector leaving that point is greater than that of the vector entering that point. Conversely, a negative divergence at a point means that the magnitude of the incoming vector is greater than that of the outgoing vector. This is best understood by the velocity field of a fluid. If at a point the fluid is leaving faster than it is coming in, then the divergence is positive, and vice versa. The mathematical form of divergence in three dimensions is:

$$\nabla\cdot \mathbf{F} = \lim_{V\rightarrow 0} \frac{1}{V} \oint\oint_{S(V)} \mathbf{F}\cdot \hat{n} dS$$