Earlier the subject of geophysics was mainly the Earth’s interior, but now the Earth’s atmosphere and neighborhood are also studied within this physics. Matter in our neighborhood, or indeed the entire solar system, is neither solid, liquid, gaseous, but plasma. In fact, 99 percent of the total matter in the universe is plasma. So understanding what plasma is is important for space physics.

Plasma is an ionized gas of charged particles with an equal number of free positive and negative charge carriers. For this reason plasma is considered quasineutral at stationary state. From the outside it looks neutral. A free particle is one whose kinetic energy is greater than its potential energy. Because of this the temperature of the plasma is also high, because temperature is a measure of kinetic energy.

In order for the plasma to be quasineutral at stationary conditions, the charges of the particles on the microscopic scale must cancel out such that the gas appears neutral on the macroscopic scale. Coulomb potential at a distance $r$ from a charge $q$

$$ \phi_C = \frac{q}{4\pi\epsilon_0 r} $$

where $\epsilon_0$ is the permittivity in free space. It must be shielded so that the potential of other charges does not fall within this potential. This shielded potential is called the Debye potential, mathematically

$$ \phi_D = \frac{q}{4\pi\epsilon_0 r} e^{-r/\lambda_D} $$

where $\lambda_D$ is the Debye length. Beyond the Debye length of a charge, i.e., if $r > \lambda_D$ , the potential decreases exponentially. Thermal kinetic energy tends to reduce neutrality, electrostatic potential energy tends to restore neutrality, and a balance between these two energies occurs at the Debye length. Debye length

$$ \lambda_D = \left(\frac{\epsilon_0 k_B T_e}{n_e e^2}\right)^{1/2} $$

where $k_B$ is the Boltzmann constant, $e$ is the electron charge, $T_e$ is the electron temperature equal to the ion temperature $T_i$, $n_e$ is the electron density equal to the ion density $n_i$. The definition of temperature can be more exact, but we will assume this relationship between average energy and temperature for now: $\langle E \rangle = k_B T$ .

To be quasineutral, the physical length of a plasma must be much greater than the Debye length, the condition being $L \gg \lambda_D$. Joint shielding of all charges will not work unless this condition is met. This condition is therefore sometimes called the First Plasma Criterion.

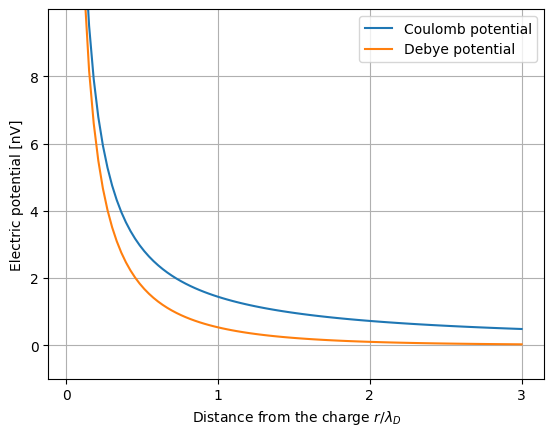
This figure compares Coulomb and Debye potentials in nanovolt units. The distance on the x axis is given in proportion to the Debye length. As can be seen, the Debye potential (orange) approaches zero much faster than the Coulomb potential (blue) beyond the Debye length.

A Debye sphere can be thought of with a radius of Debye length. In order to form a plasma, this sphere must contain a sufficient number of particles. The volume of the sphere $(4\pi/3)\lambda_D^3$ multiplied by the electron density gives the total number of particles.

$$ N = \frac{4\pi}{3} \lambda_D^3 n_e $$

where $\Lambda = \lambda_D^3 n_e$ is called the plasma parameter. This is where the Second Plasma Criterion comes from:

$$ \Lambda \gg 1 $$

That is, the total number of particles must be much greater than one. Substituting the full form of the Debye length into this equation gives

$$ n_e^{1/3} \ll k_B T_e $$

Which clarifies the meaning of the second criterion. Since the potential energy is proportional to the electron density above, the mean potential energy must be much less than the mean energy $\langle E \rangle$ .

When a quasineutral plasma is disturbed from outside, its electrons tend to return to their previous neutral state. The speed of the electron rather than the ion is being referred to because the electron is much lighter than other ions. External disturbances cause an average oscillation in plasma electrons around relatively massive ions. The frequency of this oscillation is called the plasma frequency, mathematically

$$ \omega_{pe} = \left(\frac{n_e e^2}{m_e \epsilon_0} \right)^{1/2} $$

where $m_e$ is the mass of the electron. The basic lesson of this equation is that the plasma frequency is proportional to the square root of the electron density.

A plasma like that of the Earth’s ionosphere cannot be called a pure plasma. The ionosphere contains free particles as well as many neutral atoms. Many collisions of free charges with neutrals lead to an equilibrium between the two and the plasma then behaves like a neutral gas. To prevent this, the electrons must avoid collisions. The Third Plasma Criterion is based on this condition:

$$ \omega_{pe} \tau_n \gg 1 $$

where $\tau_n$ is the average time between two collisions between an electron and a neutral. The bottom line is this: the plasma frequency must be much higher than the collision frequency.