Table of Contents
This is an old revision of the document!
VII. Magnetic force and field
1. Magnetism
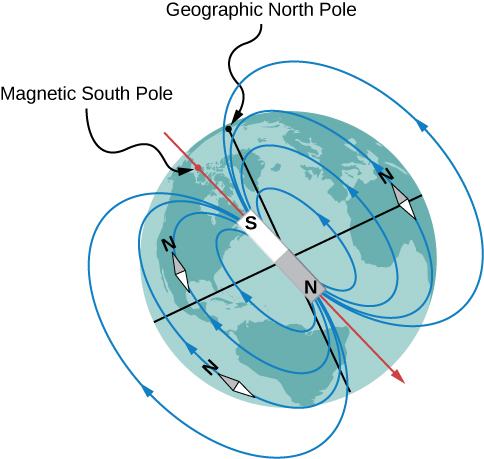
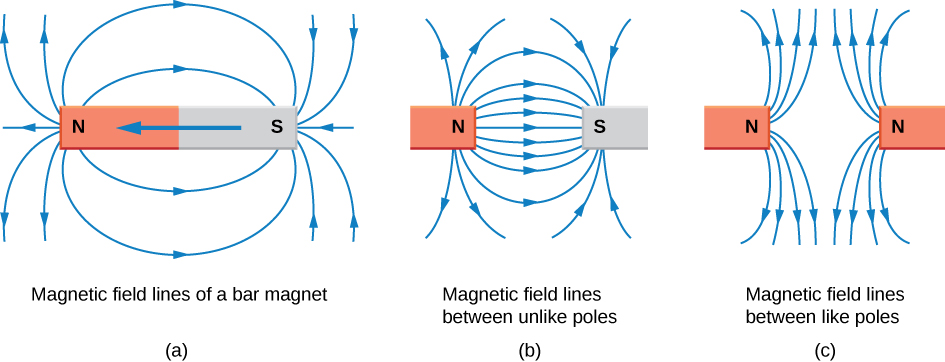
2. Magnetic fields and lines
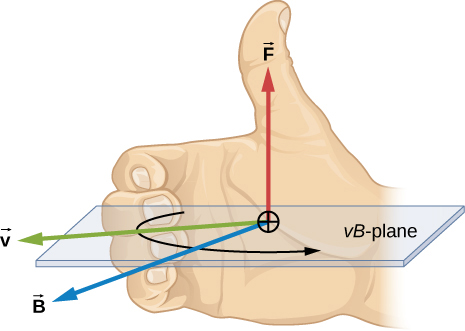
Magnetic field is defined using the magnetic force a charged particle experiences while moving in that field:
$$ \vec{F} = q \vec{v} \times \vec{B} = qvB\sin\theta $$
where $\vec{v}$ is the velocity of the particle, $\vec{B}$ is the magnetic field, and $\theta$ the angle between the two.
SI unit is tesla (T), and another unit is gauss (G). 1 G = $10^{-4}$ T.
3. Motion of a charged particle in B-field
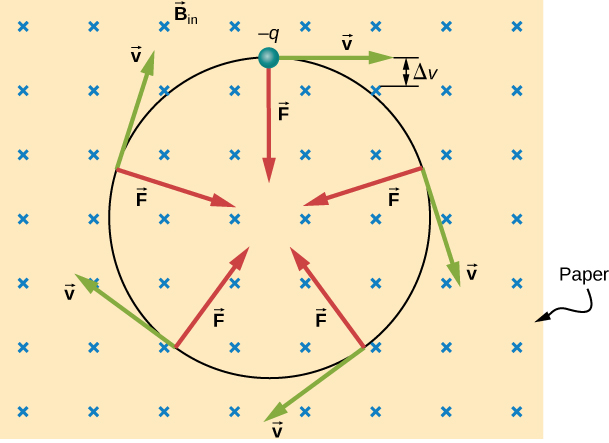
$$ F = qvB \Rightarrow \frac{mv^2}{r}=qvB \Rightarrow r = \frac{mv}{qB} $$
which is the radius of the curvature of the path of a negative charge. The period
$$ T = \frac{2\pi r}{v} = \frac{2\pi m}{qB}. $$
If the velocity is not perpendicular to the field, then we have a helical motion.
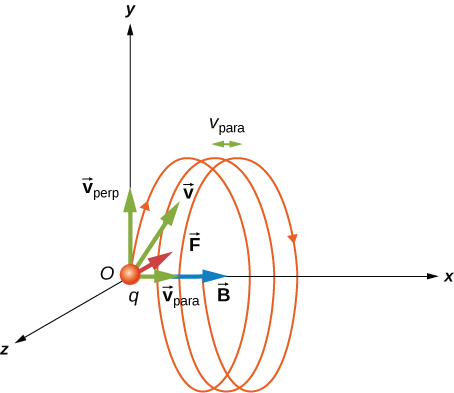
The $v_{perp}=v\sin\theta$ provides the circular motion and $v_{para}=v\cos\theta$ provides the forward motion resulting in a pitch $p=v_{para}T$.
4. Magnetic force on a current-carrying conductor
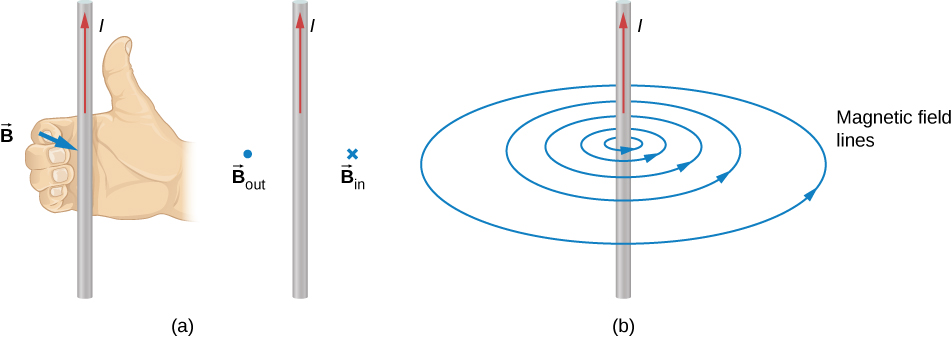
Electric current $I=neAv_d$.
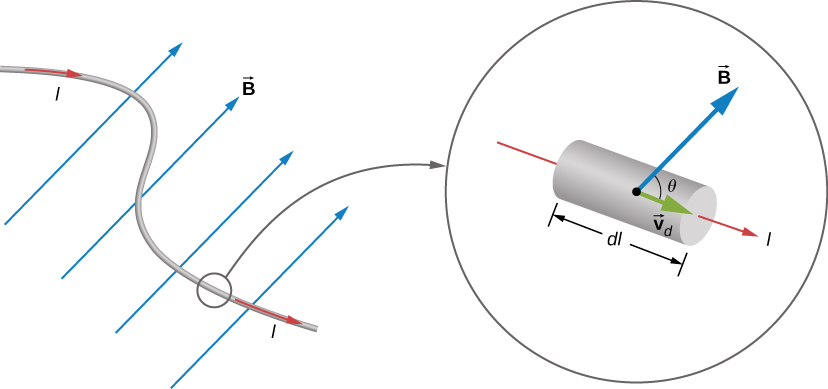
The magnetic force on a single charge is $e\vec{v}_d\times \vec{B}$. Total force on charges within the volume $nAdl$ would then be
$$ d\vec{F} = nAdle \vec{v}_d\times \vec{B}. $$
If $d\vec{l}$ is a vector pointing in the direction of $\vec{v}_d$, then
$$ d\vec{F} = neAv_d d\vec{l}\times \vec{B} = I d\vec{l} \times \vec{B}. $$
If the wire is straight and the field is uniform,
$$ \vec{F} = I \vec{l} \times \vec{B}. $$
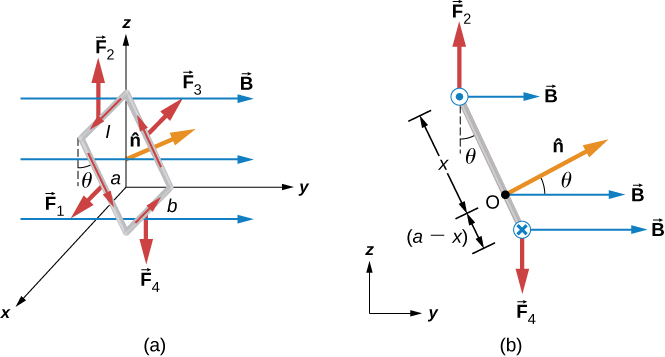
5. Force and torque on a current loop
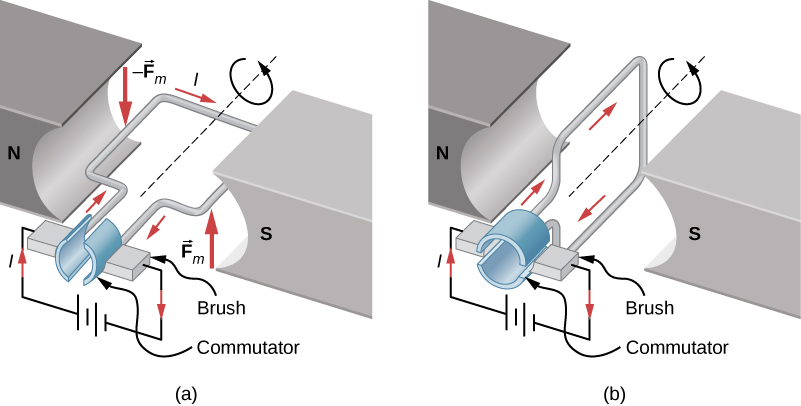
Apply $\vec{F} = I\vec{l}\times \vec{B}$ on 4 sides.