Google Colab example

Spring constant is a property of a spring; its value $k$ should be a constant. You will calculate $k$ using two different methods: first, using the extension $l$ caused by a hanging mass $m$ and second, using the period $T$ for a given hanging mass $m$.

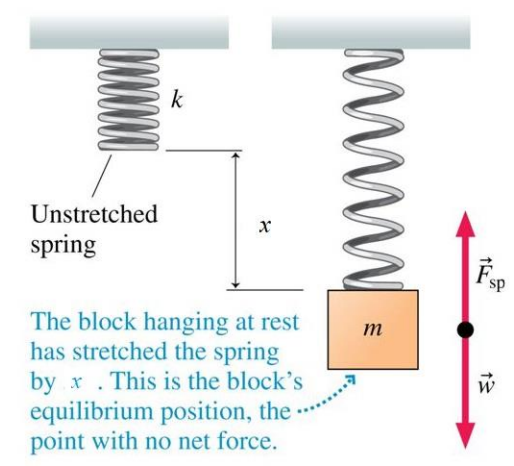
When a mass $m$ is hung from an unstretched spring, it is extended by a length $x=l$ because of the gravitational pull of the earth on the mass. The spring exerts a restoring force $F$ on the mass opposite to its gravitational force $mg$. According to Hooke’s law

$$F \propto -l \Rightarrow F = -kl$$

where $k$ is the spring constant. Replacing $F=-mg$ we get $-mg = -kl$ and

$$k = g\frac{m}{l}.$$

$$l = \frac{g}{k}m + 0$$

For the second method, you will use the relation between period and mass

$$T = 2\pi \sqrt{\frac{m}{k'}}$$

which leads to

$$k' = 4\pi^2 \frac{m}{T^2}.$$

The values $k$ and $k'$ should be very similar because they are both the spring constant of the same spring.

1. Why are $k$ and $k'$ different?
2. Which one is greater, $\delta k$ or $\delta k'$? Why?
3. In which method we have higher fitting error?