Report sample in Google Colab

$$mgh = \frac{1}{2} m r^2 \omega^2 + \frac{1}{2} I \omega^2 + n_1 W$$

$$\frac{1}{2} I \omega^2 = n_2 W \Rightarrow W = \frac{I\omega^2}{2n_2}$$

$$I = \frac{2mgh - mr^2\omega^2}{\omega^2\left(1+\frac{n_1}{n_2}\right)}$$

$$\frac{\omega+0}{2} = \frac{2\pi n_2}{t} \Rightarrow \omega = \frac{4\pi n_2}{t}$$

$$h = 2\pi r n_1$$

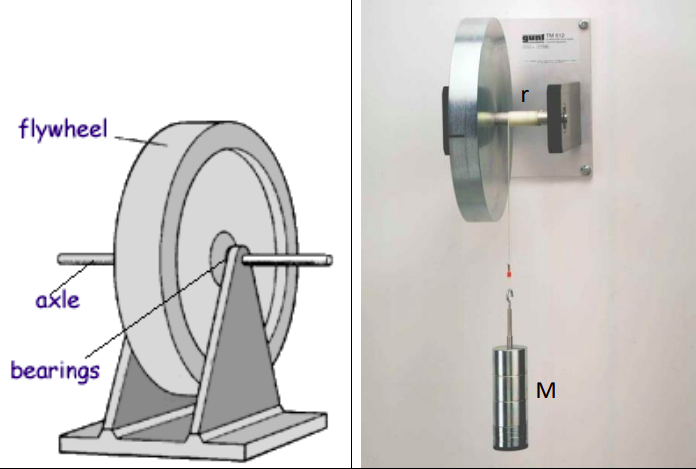
Number of rotations before the mass falls, $n_1=$

Radius of the axle, $r=[(a+vb)/2]$ cm; where $a$ is the main scale reading, $b$ is the Vernier scale reading, and $v$ is the Vernier constant.

Mean

$$\mu = \frac{1}{N} \sum_{i=0}^{N-1} x_i.$$

Standard deviation

$$\sigma = \sqrt{ \frac{1}{N} \sum_{i=0}^{N-1} (x_i-\mu)^2}.$$

1. Why does the flywheel come to a stop?
2. Why are the 4 measurements of moment of inertia different?
3. When does the flywheel reach its maximum velocity?
4. What does the standard deviation (numpy.std) of $I$ tell you?