Table of Contents
This is an old revision of the document!
ভেক্টর ফিল্ড
কোনো ফিল্ডের প্রত্যেক পয়েন্ট ব্যাখ্যা করার জন্য যদি একইসাথে একটা ম্যাগ্নিচুড ও ডিরেকশন লাগে তবে তাকে ভেক্টর ফিল্ড বলা যায়। মানে এই ফিল্ডের প্রত্যেক পয়েন্টে একটা ভেক্টর চিন্তা করতে হবে। ফিল্ডটা যেকোনো ডাইমেনশনের হতে পারে, তবে আমাদের ইউনিভার্সে ভেক্টর ফিল্ডগুলা মূলত ত্রিমাত্রিক। কিন্তু আমরা সবচেয়ে ভালোভাবে ভিজুয়ালাইজ করতে পারি দ্বিমাত্রিক ভেক্টর ফিল্ড। আইনস্টাইনের কার্ভবলে যেমন স্থানের তিন মাত্রাকে দুই মাত্রায় নামিয়ে আনতে হয়, তেমনি ইলেক্ট্রোম্যাগ্নেটিক ফিল্ডের তিন মাত্রাকে দুই মাত্রায় নামিয়ে আনলে চিন্তা করতে অনেক সুবিধা হয়।
1. গ্র্যাডিয়েন্ট
একটা স্কেলার ফিল্ড $f$কে গ্র্যাডিয়েন্টের (ন্যাবলা বা ডেল: $\nabla$) মাধ্যমে ভেক্টর ফিল্ডে ($\mathbf{F}$) রূপান্তরিত করা যায়, যার গাণিতিক রূপ নিচে তিন মাত্রার ইউক্লিডিয়ান স্পেসে কার্তেসিয়ান কোওর্ডিনেট ইউজ করে দেখানো হয়েছে।
$$ \mathbf{F} = \nabla f = \frac{\partial f}{\partial x} \hat{i} + \frac{\partial f}{\partial y} \hat{j} + \frac{\partial f}{\partial z} \hat{k} $$
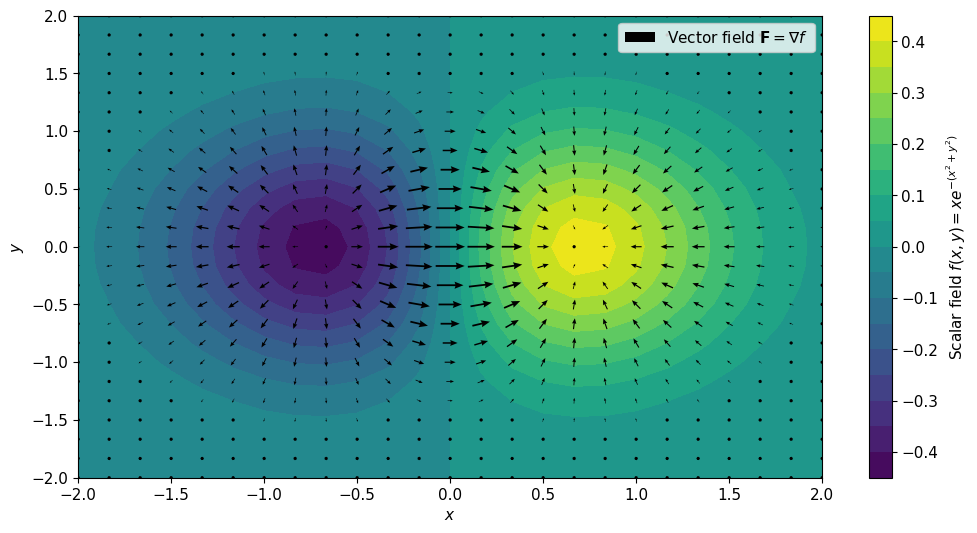
যেখানে $\hat{i},\hat{j},\hat{k}$ যথাক্রমে $x,y,z$ অর্ডিনেটের ইউনিট ভেক্টর। এর একটা দ্বিমাত্রিক ভিজুয়ালাইজেশন নিচে দেখানো হয়েছে।
উপরে কালার ইউজ করে একটা স্কেলার ফাংশন $f(x,y)=xe^{-(x^2+y^2)}$ দেখানো হয়েছে যার কালারবার ডানে দেয়া আছে। এই ফাংশনের গ্র্যাডিয়েন্ট $\nabla f$ দেখানো হয়েছে অ্যারোর মাধ্যমে, যেখানে তীরের দৈর্ঘ হলো একটা নির্দিষ্ট পয়েন্টে ভেক্টরের মান।
2. ডাইভার্জেন্স
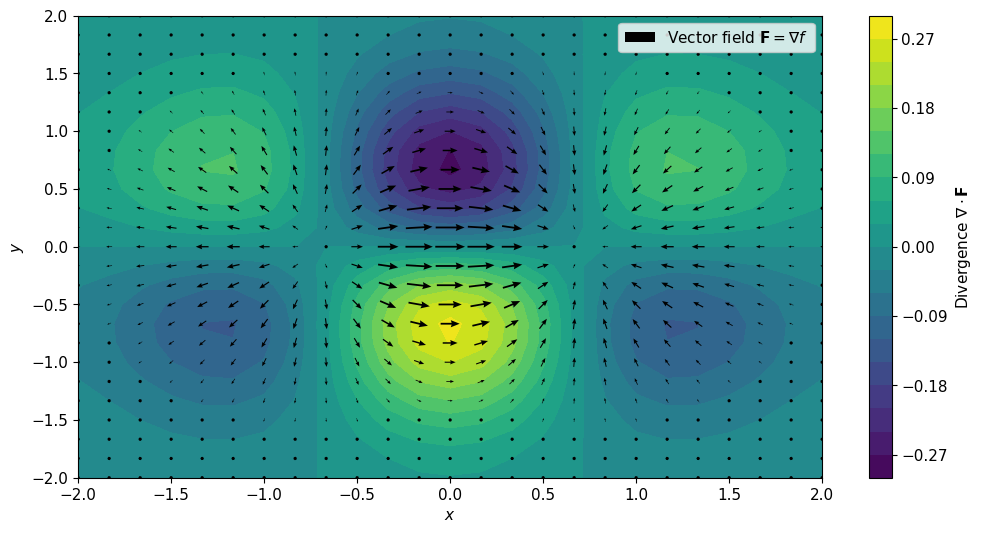
একটা ভেক্টর ফিল্ডের ভিতরে কোন জায়গায় সোর্স (আউটওয়ার্ড ভেক্টর) বা সিংকের (ইনওয়ার্ড ভেক্টর) পরিমাণ কেমন তা ডাইভার্জেন্স দিয়ে জানা যায়। ফিল্ডের কোনো পয়েন্টে ডাইভার্জেন্স পজিটিভ মানে সেই পয়েন্টে ঢুকতে থাকা ভেক্টরের চেয়ে সেখান থেকে বের হতে থাকা ভেক্টরের ম্যাগ্নিচুড বেশি। আর উল্টাভাবে কোনো পয়েন্টে ডাইভার্জেন্স নেগেটিভ মানে সেখান থেকে বের হতে থাকা ভেক্টরের চেয়ে ঢুকতে থাকা ভেক্টরের ম্যাগ্নিচুড বেশি। একটা ফ্লুয়িডের ভেলোসিটি ফিল্ড দিয়ে এটা ভালো বুঝা যায়। যদি একটা পয়েন্টে ফ্লুয়িড যত বেগে আসছে তার চেয়ে বেশি বেগে বের হয় তাহলে সেখানে ডাইভার্জেন্স পজিটিভ, এবং ভাইস ভার্সা। তিন মাত্রায় ডাইভার্জেন্সের গাণিতিক রূপ হবে এমন:
$$ \nabla\cdot \mathbf{F} = \lim_{V\rightarrow 0} \frac{1}{V} \oint\oint_{S(V)} \mathbf{F}\cdot \hat{n} dS $$
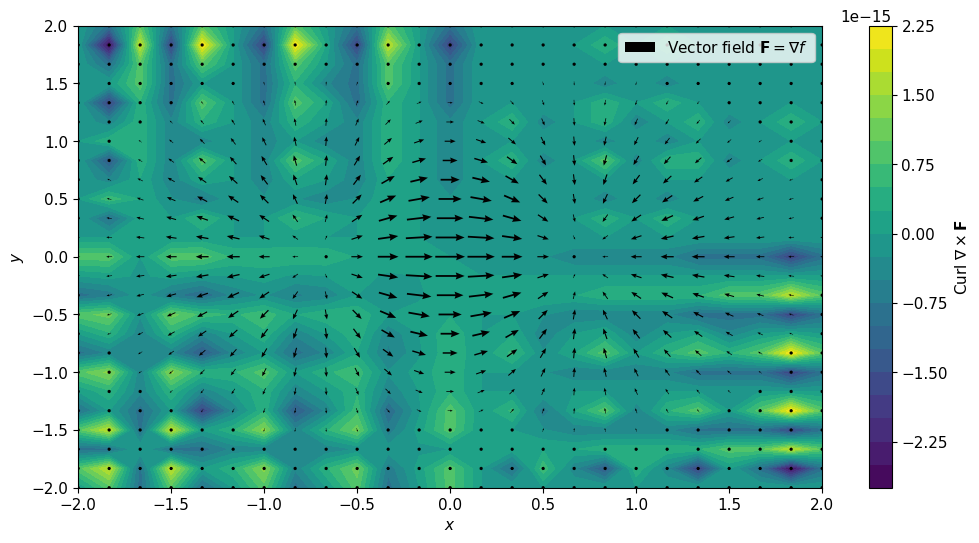
3. কার্ল