কোনো ফিল্ডের প্রত্যেক পয়েন্ট ব্যাখ্যা করার জন্য যদি একইসাথে একটা ম্যাগ্নিচুড ও ডিরেকশন লাগে তবে তাকে ভেক্টর ফিল্ড বলা যায়। মানে এই ফিল্ডের প্রত্যেক পয়েন্টে একটা ভেক্টর চিন্তা করতে হবে। ফিল্ডটা যেকোনো ডাইমেনশনের হতে পারে, তবে আমাদের ইউনিভার্সে ভেক্টর ফিল্ডগুলা মূলত ত্রিমাত্রিক। কিন্তু আমরা সবচেয়ে ভালোভাবে ভিজুয়ালাইজ করতে পারি দ্বিমাত্রিক ভেক্টর ফিল্ড। আইনস্টাইনের কার্ভবলে যেমন স্থানের তিন মাত্রাকে দুই মাত্রায় নামিয়ে আনতে হয়, তেমনি ইলেক্ট্রোম্যাগ্নেটিক ফিল্ডের তিন মাত্রাকে দুই মাত্রায় নামিয়ে আনলে চিন্তা করতে অনেক সুবিধা হয়।

একটা স্কেলার ফিল্ড $f$কে গ্র্যাডিয়েন্টের (ন্যাবলা $\nabla$) মাধ্যমে ভেক্টর ফিল্ডে ($\mathbf{F}$) রূপান্তরিত করা যায়, যার গাণিতিক রূপ নিচে তিন মাত্রার ইউক্লিডিয়ান স্পেসে কার্তেসিয়ান কোওর্ডিনেট ইউজ করে দেখানো হয়েছে।

$$ \mathbf{F} = \nabla f = \frac{\partial f}{\partial x} \hat{i} + \frac{\partial f}{\partial y} \hat{j} + \frac{\partial f}{\partial z} \hat{k} $$

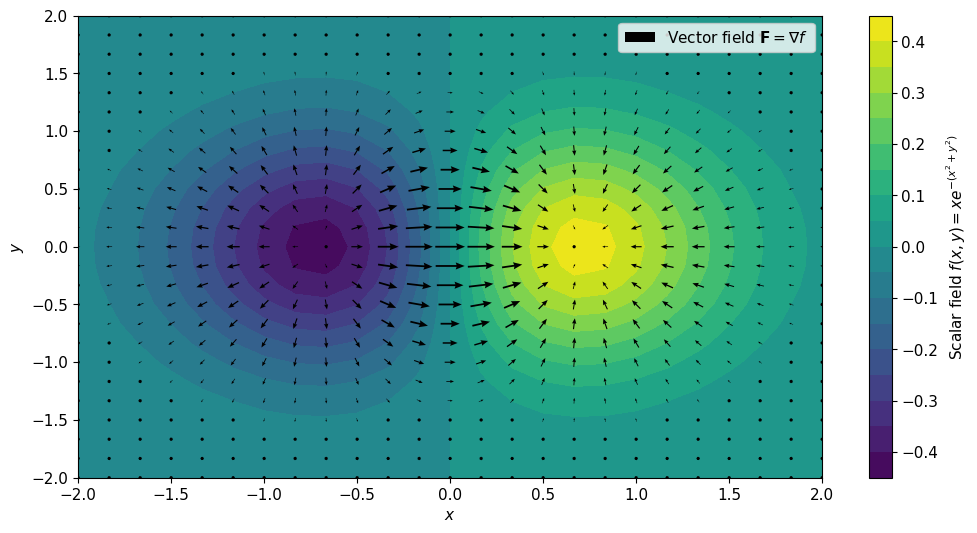
যেখানে $i,j,k$ যথাক্রমে $x,y,z$ দিকের ইউনিট ভেক্টর। এর একটা দ্বিমাত্রিক ভিজুয়ালাইজেশন নিচে।

উপরে কালার ইউজ করে একটা স্কেলার ফাংশন $f(x,y)=xe^{-(x^2+y^2)}$ দেখানো হয়েছে যার কালারবার ডানে দেয়া আছে। এই ফাংশনের গ্র্যাডিয়েন্ট $\nabla f$ দেখানো হয়েছে অ্যারোর মাধ্যমে, যেখানে তীরের দৈর্ঘ হলো একটা নির্দিষ্ট পয়েন্টে ভেক্টরের মান।