গ্রহের টেম্পারেচার প্রেডিক্ট করার সবচেয়ে সহজ উপায় তারা থেকে এবজর্ব করা আলোর সাথে রেডিয়েট করা আলোর পার্থক্য বের করা। প্যারেন্ট স্টার থেকে একটা গ্রহের এবজর্ব করা পাওয়ার

$$ P_a = \frac{L_\star}{4\pi d^2} \pi r_+^2(1-A) $$

যেখানে $L_\star$ তারার লুমিনসিটি, $d$ তারা থেকে গ্রহের গড় দূরত্ব, $r_+$ গ্রহের রেডিয়াস, এবং $A$ গ্রহের এলবিডো (০ থেকে ১ পর্যন্ত একটা নাম্বার)। গ্রহের রেডিয়েট করা পাওয়ার

$$ P_r = 4\pi r_+^2 (\epsilon \sigma T_+^4) $$

যেখানে $\epsilon$ গ্রহের এমিসিভিটি (০ থেকে ১ পর্যন্ত একটা নাম্বার), $\sigma$ স্টেফান-বোল্টজমান কনস্টেন্ট, আর $T_+$ গ্রহের ইকুইলিব্রিয়াম টেম্পারেচার। এবরজর্ব পাওয়ারের সাথে রেডিয়েট করা পাওয়ার ইকুয়েট করলে সহজেই দেখানো যায়,

$$ T_+ = \left[ \frac{L_\star(1-A)}{16\pi\epsilon\sigma d^2} \right]^{1/4} $$

এবং টেম্পারেচার থেকে কোনো গ্রহের পিক রেডিয়েশনের ওয়েভলেন্থ বের করা সম্ভব প্লাংকের ল ওয়েভলেন্থের সাপেক্ষে ম্যাক্সিমাইজ (ডেরিভেটিভ শূন্য ধরে নিয়ে) করার মাধ্যমে, অর্থাৎ ভিনের ডিসপ্লেসমেন্ট ল’র মাধ্যমে:

$$ \lambda_p = \frac{b}{T_+} $$

যেখানে $b=0.02898$ ভিনের ডিসপ্লেসমেন্ট কনস্টেন্ট। অর্থাৎ একটা গ্রহের লুমিনসিটি সবচেয়ে বেশি হবে $\lambda_p$ তরঙ্গদৈর্ঘে।

পৃথিবীর এলবিডো ০.৩০ আর এমিসিভিটি ০.৯৬ ধরে নিলে তার টেম্পারেচার হওয়ার কথা -১৫ ডিগ্রি সেলসিয়াস, যা আমাদের আসল টেম্পারেচার +১৫ ডিগ্রি থেকে ৩০ ডিগ্রি কম। বাস্তবে পৃথিবীর সার্ফেসের এভারেজ টেম্পারেচার প্রেডিকশনের চেয়ে ৩০ ডিগ্রি বেশি হওয়ার কারণ গ্রিনহাউজ ইফেক্ট। বায়ুমণ্ডলের কার্বন ডাই অক্সাইড থাকায় সূর্য থেকে আসা ভিজিবল লাইট ঢুকতে পারে, কিন্তু পৃথিবী থেকে রেডিয়েটেড ইনফ্রারেড আলো সহজে বের হতে পারে না।

সৌরজগতের আট গ্রহের মধ্যে ভিতরের ৪টা কেন রকি আর বাইরের ৪টা কেন গ্যাসি তা সূর্যের টেম্পারেচার ও সৌরজগতের ইতিহাস দিয়ে ব্যাখ্যা করা যায়। প্রায় পাঁচ বিলিয়ন বছর আগে এখানে গ্রহের জন্ম হয়েছে সূর্যের চারদিকে ঘুরতে থাকা প্রটোপ্ল্যানেটারি ডিস্কের ছোট ছোট কণা জমাট বেঁধে জড়ো হওয়ার মাধ্যমে। সূর্যের কাছে তাপমাত্রা বেশি হওয়ায় গ্যাস জমাট বাঁধতে পারেনি, যেসব যৌগের মেল্টিং পয়েন্ট অনেক বেশি শুধু তারাই জমাট বেঁধেছে। তাই সূর্যের কাছের গ্রহ সিলিকেটের মতো জিনিসে তৈরি। সূর্য থেকে দূরে তাপমাত্রা কম হওয়ায় গ্যাসও জমাট বাঁধতে পেরেছে। তবে অন্যান্য তারার চারদিকে একই কথা সত্য নাও হতে পারে। অনেক প্ল্যানেটারি সিস্টেমে জুপিটারের মতো গ্যাস জায়ান্ট পাওয়া গেছে তারার খুব কাছে।

যেকোনো গ্রহ জন্মের পর পর বেশি গরম থাকে, যেসব ছোট ছোট প্ল্যানেটেসিমাল জড়ো হয়ে তার জন্ম হয়েছে তাদের কলিশন থেকে তৈরি তাপের কারণে। দিন দিন বিকিরণের কারণে এই তাপ কমতে থাকে। একটা গ্রহের মোট থার্মাল এনার্জি তার রেডিয়াসের কিউবের সমানুপাতিক, আর তার রেডিয়েশনের কারণে এনার্জির লস তার সার্ফেস এরিয়া, মানে রেডিয়াসের বর্গের সমানুপাতিক। ইন্টার্নাল এনার্জি দিয়ে রেডিয়েটেড এনার্জি ভাগ করে ডাইমেনশনাল এনালাইসিসের মাধ্যমে দেখানো যায়, একটা গ্রহের কুলিং রেইট (হিট হারানোর হার) রেডিয়াসের ব্যস্তানুপাতিক ($r^2/r^3=1/r$)। এই কারণে ছোট গ্রহ বুধ ও মঙ্গল বা আমাদের চাঁদ অনেক আগেই এনার্জি হারিয়ে ঠাণ্ডা হয়ে গেছে, কিন্তু পৃথিবী ও মঙ্গল এখনো ইন্টার্নাল এনার্জির কারণে এক্টিভ আছে। এই কারণে পৃথিবীর তুলনায় চাঁদ ও মঙ্গলের সার্ফেস অনেক পুরানো, অনেক দিন যাবৎ সেখানে বড় কোনো পরিবর্তন ঘটেনি।

তারা যে কারণে গোল গ্রহ গোল হওয়ার কারণ অনেকটা একই রকম। নিচের ডায়াগ্রামে একটা গ্রহের কেন্দ্র থেকে $r$ দূরত্বে অবস্থিত $\delta r$ পুরুত্বের একটা স্ল্যাবের উপর মোট গ্র্যাভিটেশনাল ফোর্স ($F_g$), এবং কেন্দ্রের দিকে চাপ $P(r+\delta r)$ ও সার্ফেসের দিকে চাপ $P(r)$ দেখানো হয়েছে।

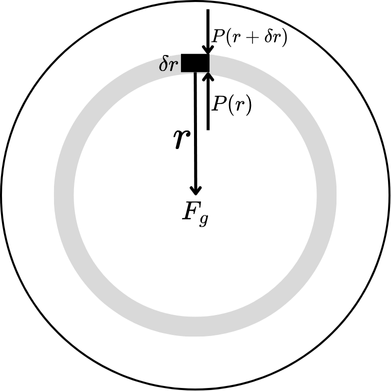
ভিতরের দিকে চাপের তুলনায় বাইরের দিকে চাপ বেশি হতে হবে, নয়ত গ্র্যাভিটেশনাল ফোর্সের বিপরীতে একটা নেট কেন্দ্রবিমুখী চাপ পাওয়া যাবে না। গ্রহ যদি ইকুইলিব্রিয়ামে থাকে, তাহলে তিনটা ফোর্সের যোগফল শূন্য হতে হবে: $ P(r)A - P(r+\delta r)A - F_g = 0 $, যেখানে $A$ স্ল্যাবের সার্ফেস এরিয়া এবং কেন্দ্রের দিকে বল নেগেটিভ ধরা হয়েছে। তাহলে

$$ P(r)A - P(r+\delta r)A - \frac{GM_r (A\rho\delta r)}{r^2} = 0 $$

যেখানে $M_r$ হচ্ছে $r$ রেডিয়াসের ভিতরে গ্রহের মোট ভর, $\rho$ গ্রহের ঘনত্ব (যা ইউনিফর্ম ধরা হয়েছে), এবং $A\rho\delta r$ স্ল্যাবের ভর। এই ইকুয়েশনের দুই পাশ স্ল্যাবের এরিয়া দিয়ে ভাগ করে $P(r) - P(r+\delta r) = \delta P$ বসালে পাওয়া যায়:

$$ \frac{\delta P}{\delta r} \sim \frac{dP}{dr} = \frac{GM_r\rho}{r^2} $$

যেখানে স্ল্যাবের পুরুত্ব ইনফিনিটেসিমাল ধরে ডেরিভেটিভটা পাওয়া গেছে। ঘনত্ব কনস্টেন্ট ধরে নিলে $M=4\pi\rho r^3/3$, এবং সেক্ষেত্রে

$$ \frac{dP}{dr} = \frac{4\pi G}{3} \rho^2 r $$

যা হাইড্রোস্টেটিক ইকুইলিব্রিয়ামের ইকুয়েশন নামে পরিচিত। এই ডিফারেনশাল ইকুয়েশন থেকে ইন্টিগ্রেশনের মাধ্যমে গ্রহের কেন্দ্র থেকে যেকোনো দূরত্বে প্রেশার বের করা যায়। সার্ফেসে (মানে $r=R$ দূরত্বে) প্রেশার শূন্য হলে $r$ দূরত্বে প্রেশার

$$ P = \frac{2\pi G \rho^2}{3} (R^2-r^2) $$

যেখানে $R$ গ্রহের রেডিয়াস। এখানে $r=0$ বসালে গ্রহের কেন্দ্রের চাপ পাওয়া যাবে।

পৃথিবির সার্ফেস থেকে কত নিচে গেলে প্রেশার এত বেশি হয় যে পাথরও গলে যায় এই ইকুয়েশন দিয়ে তাও বের করা সম্ভব। আমরা জানি, পাথরের ক্রিটিকেল প্রেশার ১ বিলিয়ন প্যাসকেল। পৃথিবীর কেন্দ্রে প্রেশার প্রায় ১৭০ বিলিয়ন প্যাসকেল। উপরের ইকুয়েশনে $P=10^9$ বসালে দেখা যাবে, $r=6352$, মানে কেন্দ্র থেকে এই দূরত্বে পাথর গলে যায়। অর্থাৎ সার্ফেস থেকে ১৮ কিমি নামলেই পাথর গলা শুরু করে। ঘনত্ব কনস্টেন্ট ধরায় এই হিসাব কিছুটা ভুল। আসলে পৃথিবীর সার্ফেস থেকে ২৫ কিমি নিচে গেলে আমরা গলিত পাথর পেতে শুরু করি। পাথর যেখানে পাথরের মতো আচরণ করে উপরের সেই ২৫-কিমি লেয়ারের নাম লিথোস্ফিয়ার, তার নিচে প্রায় ১০০ কিমি পুরু এস্থিনোস্ফিয়ার।