Dipole antenna

The simplest radiator of electromagnetic waves (hereafter ‘light’) is a short dipole, which was used for this purpose by Hertz for the first time, in 1887. Short, because its physical length is much shorter than the wavelengths at which it transmits or receives light.

Here is a Hertzian dipole that generates radio light due to an oscillating current $I$. It is called a dipole because the currents in the two conductors are exactly out of phase, they have a $180^\circ$ phase shift. Now the alternating current (AC) $ I = I_0 \cos \omega t $ is better expressed in exponential notation:

$$ I = I_0 e^{-i\omega t} $$

where $e^{-i\omega t} = \cos\omega t - i\sin\omega t$. The current $I=dq/dt$ can be rewritten as $I=(dq/dz)(dz/dt)=(dq/dz)v$ for a wire or rod on the $z$ axis. Here $v$ is the drift velocity of the electrons. Note that the electrons flow like water molecules in a hose, very slowly, but that does not hinder current.

Now using the perpendicular electric field ($E_\theta$) derived in the article radiation from acceleration, we can find that

$$ dE_\theta = \frac{dq}{dz}dz \frac{a\sin\theta}{rc^2} = dz \frac{I}{v} \frac{-i\omega v \sin\theta}{rc^2} = \frac{-i\omega\sin\theta}{rc^2} I dz $$

because the electron acceleration for a sinusoidal current $a=-i\omega v$. The current must be modified as per the properties of the conductor. The current will decrease toward the end of the conductors and become exactly zero at the very end:

$$ I = I_0 e^{-i\omega t} \left(1-\frac{z}{l/2}\right) $$

whose integral can be approximated as

$$ \int_{-l/2}^{l/2} I dz \approx \frac{I_0 l}{2} e^{-i\omega t} $$

which we have to put back in the equation of $E_\theta$. Also we can replace $\omega$ with $2\pi c/\lambda$ and finally get

$$ E_\theta \approx \frac{-i\pi\sin\theta}{c} \frac{I_0 l}{\lambda} \frac{1}{r} e^{-i\omega t} $$

which we can use to finally calculate the time-averaged Poynting flux

$$ \langle S \rangle = \frac{c}{4\pi} \frac{1}{2} \left(\frac{\pi l I_0}{c\lambda}\right)^2 \frac{\sin^2\theta}{r^2} $$

where the factor $1/2$ is singled out because it somes from $\langle \cos^2\omega t \rangle = \langle \cos^2\omega t \rangle = 1/2$ and here we have used the fact that $\sin^2\omega t + \cos^2\omega t = 1$. Now in the acceleration article we have used power to denote the integration of this flux over the surface of an area. But when we use the phrase power pattern of a dipole radiator we actually mean the flux toward different angular directions normalized to unity at the peak. In this sense

$$ P \propto \sin^2\theta $$

just as the flux $S\propto \sin^2\theta$ for a single accelerated charge. A short dipole behaves just like a point charge in this sense. If we want to find the total time-averaged power we have to perform a similar integration as we did in the acceleration article:

$$ \langle P \rangle = \int \langle S \rangle dA = \frac{\pi^2}{3c} \left(\frac{I_0l}{\lambda}\right)^2 = \frac{\pi^2}{3c} (I_0 l_\lambda )^2 $$

where $l_\lambda=l/\lambda$ is the length of the dipole in units of wavelengths. Most practical antennas are half-wave dipoles, meaning their $l=\lambda/2$ and $l_\lambda=0.5$, because they are resonant. Each of their conductors is $\lambda/4$ in length.

A ground-plane vertical is made using just the upper conductor, the lower is imagined to be the earth as the ground place. If you want to build an AM radio station broadcasting at 1 MHz ($\lambda\sim 300$ m), you might use a 75 m high tower insulated from the ground. The ground acts like a mirror.

In order to get an intuition, see this animation showing the sweeping of waves by dipole current. You can see that the light transmitted by dipoles is always polarized along the direction of the dipole.

In astronomy, we do not transmit radio light, we receive them. But the transmission and reception are like twin sisters, identical. Astronomers almost always use half-wave dipoles or ground-plane verticals. A telescope has three parts: collector, detector and processor. The large parabolic dishes you see so often work only as collectors or gatherers of light by focusing them onto a focal plane. The actual ‘antenna’ sitting at the focal plane is called a feed and we are referring to these feeds when we say astronomers use half-wave dipoles and ground-plane verticals.

The word feed came from radar technology where the feeds actually feed light onto the large reflectors for the final transmission. Radio astronomy is the opposite of radar technology. Here the feed actually does not feed the dish but the dish feeds the feed. Maybe we should have called it fed instead of feed.

At frequencies below 1 GHz or wavelengths above 0.3 m, we use half-wave dipoles as feeds. Here each half of a conductor is $\lambda/4$ long, and the reflector dish is also located at a distance of around $\lambda/4$ behind them to orient the power pattern parallel to the main dish. But the same cannot be done at shorter wavelengths.

Ground-plane verticals located inside waveguide horns are used at shorter wavelengths. The waveguide guides the desired waves onto the feed which is inserted though a whole. The lower half does not exist as it is a quarter-wave ground-plane vertical.

The side walls are separated by slightly more than $\lambda/2$ and the top and bottom walls separated by slightly less than $\lambda/2$. This will only detect vertical polarization.

The power pattern of a dipole is also called response pattern in astronomy. Here light induces a current and voltage. The power pattern is related to the voltage pattern.

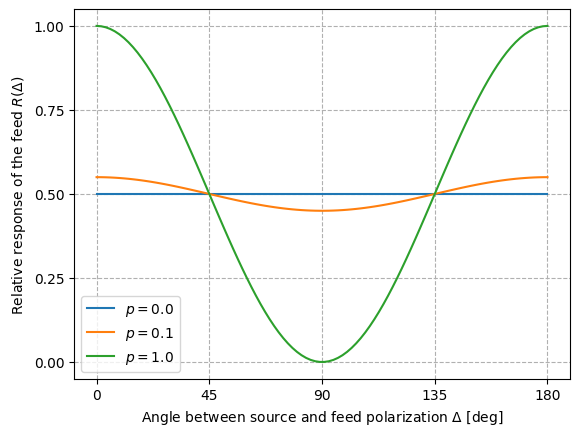
The response of a telescope $R\propto \cos \Delta$ where $Delta$ is the angle between the electric fields of the source and the feed. So we can detect the polarization of the light of an astronomical source by rotating a linearly polarized feed. If the polarization degree of a partially polarized source

$$ p = \frac{I_p}{I} = \frac{I_p}{I_u+I_p} $$

where $I_u$ and $I_p$ are the unpolarized and polarized parts, then the response of our feed

$$ R \propto I_p\cos^2\Delta + \frac{I_u}{2}. $$

whose behavior is shown below.

The polarization degree can be expressed as a function of the parallel and perpendicular component of the response.

$$ p = \frac{R_\parallel-R_\perp}{R_\parallel+R_\perp}. $$