Table of Contents
1. Stars in equilibrium
Stars like the Sun remain stable (do not expand or shrink) for almost 10 billion years. In this chapter, we will explore seven issues related to stars in equilibrium as listed below.
- Condition for condensation
- Requirement for equilibrium
- Balance of kinetic and potential energies
- Timescales for different changes
- Nuclear reactions
- Limiting luminosity
- Instability and pulsations
1. Condition for condensation
Stars form from the condensation of gas cloud in the interstellar medium (ISM; see NASA Eyes). A condensing cloud must become dense enough for starting nuclear reactions. As a cloud condenses, it sheds angular momentum and must overcome the pressure of magnetic fields inherent in the ionized gas of the ISM.

Many bubbles of perturbation (higher density) can arise within a single cloud. The condition for such a perturbation to collapse (contract toward its own center) is simply that the magnitude of the gravitational potential energy ($E_p$) of an average atom in the cloud must be greater than its kinetic energy ($E_k$):
$$ E_k \lesssim |E_p|. $$
The average kinetic energy of an atom in a hydrogen cloud is around $(m_Hv^2)$ where $m_H$ is the mass of a hydrogen atom and $v$ its velocity. The magnitude of its gravitational potential energy is $(GMm_H/R)$ where $M$ is the mass of the cloud and $R$ its radius. Remembering from the definition of density ($\rho$) that $M\approx \rho R^3$, it can be demonstrated that a cloud will collapse if its size is greater than
$$ R \approx \frac{v}{\sqrt{G\rho}}. $$
It turns out the kinetic speed $v$ of particles in a gas is very close to the speed of sound $v_s$ in that gas. Thus we write Jeans length (click for full derivation)
$$ \lambda_J \approx \frac{v_s}{\sqrt{G\rho}}. $$
So the collapse is primarily dictated by density.
We can also find a critical mass or Jeans mass
$$ M_J \approx \left(\frac{kT}{Gm_{av}}\right)^{3/2} \frac{1}{\sqrt{\rho}} $$
which can be derived in two separate ways: either from the collapse criterion given in the beginning (replacing $mv^2\approx kT$) or from the Jeans length, replacing $v_s^2 = 5kT/(3m_{av})$. Try at home and derive in the class together. Always drop factors of order unity.
Calculate critical mass and length for the Cold Neutral Medium (CNM) of the ISM (the required values are given in the UV article) using Google Colab. What if the size of the cloud decreases hundred-fold? What is the critical mass and length in the intergalactic medium (IGM) where $n_H \sim 100$ m$^{-3}$ and $T\sim 3\times 10^4$ K?
In the CNM, Jeans length is around 60 ly, and Jeans mass more than 4000 $M_\odot$. As the CNM clouds are in reality less than 30 ly in size, they will not collapse. But if such a cloud would shrink hundred-fold, the critical mass would become only $3$ $M_\odot$. Large clouds become fragmented into many cloudlets. Each cloudlet can give rise to a star. A star cluster can form from a cloud.
For the IGM, critical mass can be almost $10^9$ $M_\odot$ which is the typical size of a galaxy.
2. Requirement for equilibrium

A gas element with thickness $dr$ is at a distance $r$ from the center of a star. At this distance, the density of the gas is $\rho(r)$. If $dP=P_2-P_1$ is the pressure differential, then the net upward force on the element
$$ F_P = -A \ dP $$
where plus is outward from the center and vice versa. The condition for hydrostatic equilibrium is
$$ F_G + F_P = 0 \Rightarrow F_G = A \ dP. $$
The gravitational force on the mass element, $dm=\rho A \ dr$, would be
$$ F_G = \frac{-GM(r)\rho(r) A \ dr}{r^2} $$
where $M(r)$ is the mass within the radius $r$. Mass outside $r$ does not contribute to the force, which can be demonstrated using Gauss's law. Now replacing this force in the above equation yields
$$ \frac{dP}{dr} = \frac{-G M(r) \rho(r)}{r^2} = -\rho(r) g(r) $$
which is the most widely used form of hydrostatic equilibrium. Here the gravitational acceleration $g(r)=GM(r)/r^2$.
3. Balance of kinetic and potential energies
If a system of particles is in stable equilibrium bound by gravity, then the virial theorem relates its total kinetic and potential energy:
$$ 2\sum E_k + \sum E_p = 0. $$
So the total energy $E=0.5 \sum E_p = -\sum E_k.$ It is valid for any potential that varies inversely with distance, such as the gravitational potential.
A simple demonstration of the theorem comes from a satellite of mass $m$ orbiting the Earth of mass $M$ in a circular orbit of radius $r$. Its kinetic energy
$$ E_k = \frac{1}{2} mv^2 = \frac{1}{2} \frac{F_r}{a_r} v^2 = \frac{1}{2} \frac{GMm}{r^2} \frac{r}{v^2} v^2 = \frac{GMm}{2r} = - \frac{1}{2} E_p. $$
Total energy of a satellite decreases due to atmospheric drag. The satellite moves to lower radius, decreasing the potential energy in the negative direction (increasing in magnitude). As kinetic energy is opposite to potential energy, the kinetic energy increases and the satellite speeds up. But as kinetic energy is only half of the potential energy, the total energy still decreases.
Derive virial theorem from hydrostatic equilibrium.
3.1 Stars

If a star did not have any nuclear energy source, it would act like the satellite you saw above. Due to the loss of energy from the surface, it would shrink, $E_p$ would become more and more negative, $E_k$ would be increasing.
Temperature would rise due the increase in kinetic energy. Star heats up. The star is giving away more potential energy than is needed for decreasing the total energy, and the extra potential energy is getting converted to kinetic energy resulting in a higher temperature. The star has a negative specific heat as the removal of heat makes it hotter. This is a quasi-stable equilibrium.
The virial theorem works its magic only during the birth and death of a star. During the birth, the cloud shrinks, $E_k$ increases resulting in faster rotation, temperature increases resulting in higher pressure. The faster rotation opposes further shrinkage via centrifugal forces and the hotter gas opposes the same via higher outward pressure. The collapse may temporarily stop only to resume again when more energy and angular momentum is lost.
During the death, the star runs out of hydrogen for nuclear fusion at the center leading to the shrinkage of the core. As the core shrinks, it heats up leading to the optimum temperature for burning helium at the core. After helium runs, further shrinkage causes even heavier elements to be produced at the core.
But when a star is in a real equilibrium, the nuclear burning at its core produces as much energy as is lost from its surface in a year. And this is only ten millionth of the total energy of the sun. A star remains in hydrostatic equilibrium.
3.2 Galaxy clusters
The image of the galaxy cluster SMACS J0723.3–7327 taken by JWST.

A cluster may have thousands of galaxies and much more intergalactic gas and dark matter. The total mass of a galaxy can be calculated using the virial theorem because clusters also obey the theorem. But there is a discrepancy.
The total kinetic energy of the cluster is calculated by measuring the mass and velocity dispersions of the member galaxies. Mass is measured from the luminosity. The total potential energy can be calculated by measuring the mass and position of the galaxies. Total $E_k$ should be half of total $E_p$, but we find that kinetic energy is much higher. There must be much more mass hidden somewhere in the cluster which is dubbed dark matter. More than 90% of the total mass of a cluster could be in the dark matter.
According to the virial theorem
$$ 2\sum_i \frac{1}{2} m_i v_i^2 - \sum_i \sum_{j \ne i} \frac{Gm_im_j}{r_{ij}} = 0. $$
If the cluster has $N$ identical galaxies each with mass $m$, then
$$ m \sum_i v_i^2 - G m^2 \sum_i \sum_{j \ne i} \frac{1}{r_{ij}} = 0. $$
Now multiply the first term by $N/N$ and the second term by $N^2/N^2$:
$$ Nm \left[\frac{1}{N} \sum_i v_i^2\right] - G \frac{(Nm)^2}{2} \left[\frac{1}{N(N-1)/2} \sum_i \sum_{j \ne i} \frac{1}{r_{ij}} \right] = 0 $$
where we assume $N(N-1)\approx N^2$ because $N$ is large. The factor $N(N-1)/2$ comes from the combination of two items from a total of $N$ items: $_NC_2=N!/[2!(N-2)!]=N(N-1)/2$. If total mass $M=Nm$ then
$$ M \langle v_i^2 \rangle_{av} - G\frac{M^2}{2} \langle r_{ij}^{-1} \rangle_{av} = 0$$
and hence the virial mass of a cluster
$$ M = \frac{2\langle v_i^2 \rangle_{av}}{G \langle r_{ij}^{-1} \rangle_{av}}. $$
The velocities are calculated by measuring the line-of-sight (los) component of the velocity via Doppler shift. If all directions are equally probable, then all three components of the velocity vector can be considered equal. So
$$ \langle v_i^2 \rangle_{av} = 3 \langle v_{i,\text{los}}^2 \rangle_{av}. $$
The positions $r_{ij}$ must be corrected for projection effects.
4. Timescales for change
Now that we can describe a star in equilibrium, we will check how long it takes for a star to change once its equilibrium is destroyed.
- Thermal timescale is related to evolution in the absence of nuclear burning.
- Dynamical timescale relates to the collapse of a star in the absence of equilibrium.
- Diffusion timescale dictates the path of radiation from the center to the surface.
4.1 Thermal timescale
Another name for the Kelvin-Helmholtz timescale, which is the time it would take for a star to radiate away all its kinetic (thermal) energy as radiation. The thermal timescale
$$ \tau_k \approx \frac{\sum E_k}{L} $$
where $L$ is the luminosity (power) of the star. The kinetic energy is half the magnitude of the total potential energy and the total $E_p$ can be found by summing the potential energies of all the pairs of particles as in the example of galaxy clusters above. We can write
$$ \sum E_p = -2\sum E_k = -\frac{GM^2}{R} $$
where $M$ and $R$ are the mass and radius of the star, repsectively. So
$$ \tau_k \approx \frac{GM^2}{RL}. $$
If nuclear burning inside the sun sops today, it would take only around 30 My for the sun to radiate away all its energy and die. But we know that the sun is more than 4.5 Gy old because the age of earth is already 4.5 Gy. Therefore, there must be another source of energy inside the sun that is sustaining it for longer than the Kelvin timescale allows.
4.2 Dynamical timescale
The timescale within which a star would collapse to its center if there was no outward opposing force. In order to derive this, assume a small test mass $m$ on the surface of a star of mass $M$ and radius $R$. If $g$ is considered constant (unrealistically) throughout the interior of the star, the inward radial acceleration of the mass
$$ a = \frac{F}{m} = \frac{GM}{R^2}. $$
The time needed to fall by a distance $R$ is found from the constant-force expression $s=at^2/2$, i. e. the dynamical timescale
$$ \tau_{in} = \sqrt{\frac{R}{a}} = \sqrt{\frac{R^3}{GM}} $$
where density $\rho=M/R^3$ giving rise to
$$ \tau_{in} = (G\rho)^{-1/2}. $$
For the sun, density is around 1400 kg m$^{-3}$. So the time is around 50 minutes. It reduces to around 20 min if you consider the variation of density inside the sun.
A white dwarf with mass equal to the sun, but a size of only 1 per cent that of the sun would be almost a million times more dense than the sun. How quickly would it collapse? What about an even denser star with nuclear densities of around a billion kg per cubic meter?
4.3 Diffusion timescale
The time it takes for a photon to reach the surface from the center. It takes time because of countless scattering and/or absorption-reemission (Thomson scattering). The timescale can be derived using a random walk.
Let us begin with a 1D photon random walk. Start the phtoton from $x=0$, flip a coin, move it to the right if the result is a head, to the left if it is a tail, always by a distance $\Delta x=l$. After 100 steps, $x\ne 0$ because of statistical fluctuation in the number of heads ($N_h$) and tails ($N_t$). If $N=N_h+N_t$ then
$$ x = Nl = (N_h-N_t)l $$
which is never zero. Averaging over many such 100-step trials would lead to an expected value of zero:
$$\langle x\rangle = \langle N_h-N_t \rangle l \approx 0$$
but the standard deviation (root-mean-square: rms) of $x$ is not zero. As the number of heads or tails follow Poisson distribution. If there are around 50 heads on average, $N_h=50$ and the uncertainty is $\Delta N_h = \surd{N}\approx 7$. So
$$ \Delta N = \sqrt{(\Delta N_h)^2+(\Delta N_t)^2} = \sqrt{N_h+N_t} = \surd N. $$
Even though the mean displacement is zero, the actual displacements will be distributed around the mean in a Gaussian distribution where the true displacement is the rms displacement
$$ x_{rms} = \sqrt{N} l. $$
For many 100-step trials, the photons go as far as $10l$, for 100-step trials $32l$, some in the one direction, some in another. Many photons start out from the center of a star. As time goes on, $N$ increases leading to a higher $x$. Plot various Gaussians here to understand this process of diffusion.
The number of photons required to reach a distance $x$ with $l$-sized steps:
$$ N\approx \left(\frac{x}{l}\right)^2. $$
In three dimensions,
$$ R_{rms}^2 = x_{rms}^2 + y_{rms}^2 + z_{rms}^2 = Nl^2 \Rightarrow N\approx \left(\frac{R}{l}\right)^2. $$
Factoring in the speed of a photon, we find the diffusion time
$$ \tau_{out} = \frac{Nl}{c} = \frac{R^2}{cl} $$
which cannot be calculated for the sun without knowing the typical step-size $l$ which is the mean free path, the average distance a photon remains free between any two collisions. It can be calculated from the Thomson cross section
$$ \sigma_T = \frac{8\pi}{3} r_e^2 $$
where the classical radius of an electron
$$ r_e = \frac{1}{4\pi\epsilon_0} \frac{e^2}{m_e c^2}. $$
The mean free path $l=(\sigma_T n_e)^{-1}$ where $n_e$ is the number density of scattering electrons, which is equal to the number of protons for a completely ionized gas. The mass is completely dominated by protons. So $n_e = \frac{M/R^3}{m_p}$. Thus we find
$$ l \approx \frac{m_p R^3}{\sigma_T M} $$
which results in
$$ \tau_{out} = \frac{\sigma_T}{cm_p} \frac{M}{R}. $$
For solar values, it is around 10 ky. The actual value is around 20 ky due to delays caused by absorption and emission.
The luminosity of the sun can be estimated from the diffusion time. Just divide the total amount of energy by the total diffusion time, to get the power in joules per s, or watts:
$$ L_\odot = \frac{aT^4 (4\pi R_\odot^3)/3}{\tau_{out}} \approx 10^{27} \text{ W} = 1 \text{ RW} $$
which is 1 ronna watts, or an octillion watts, or 1000 YK.
Photons have a thousand times less energy than the particles in the sun. So we need 1000 times more time to remove all energy of the sun if it was completely made of photons. A thousand times the diffusion timescale is indeed the thermal timescale.
5. Nuclear reactions
The energy lost from the surface is in reality replaced by the energy produced via nuclear reactions at the core.
The stable equilibrium in a star is maintained by a negative feedback mechanism. If the star shrinks due to the excess of inward gravity over the outward pressure, temperature increases and nuclear energy output at the core increases due to higher particle flux and velocities. The increased energy causes the star to expand balancing the contraction due to gravity. On the other hand, if the star expands due to an excess of outward pressure over gravity, the temperature decreases reducing the nuclear energy output at the core causing the star to shrink balancing the expansion.
A star is mostly made of hydrogen which is completely ionized. So the star actually just have free protons and electrons. The main mechanism of nuclear burning is the proton-proton interaction. But it turns out the average kinetic energy of the protons is not high enough to overcome the Coulomb barrier that exists between the protons due to repulsive electromagnetic force. The kinetic energy is 1000 times less than required.

The solution is quantum tunneling. In the figures above $y$ axis is the energy of a proton and $x$ axis the distance to another approaching proton. The square-well shows the nuclear potential and the sloping sides the $r^{-1}$ Coulomb potential. Figure (a) shows the classical picture. The protons with kinetic energy $E_1$ and $E_2$ are unable to come close enough for the strong force to act, only the proton with $E_3$ can fall into the strong well classically. But protons do not have energy as high as $E_3$. Figure (b) shows quantum tunneling. At 10 MK, there are enough protons in the tail of the Maxwell-Boltzmann distribution for tunneling or leakage into the well.
Only 1 in 20 million photons can escape from the surface of the sun as radiation. So the nuclear energy has to replenish a very small amount of energy compared to the total thermal energy of a star. A star is not primarily a nuclear furnace, but a thermal furnace. The nuclear warmer of the sun has power of 400 YW (yotta watt) which is close the luminosity of the sun, 1000 YW.
5.1 Proton-proton chain
Helium nuclei can be produced from hydrogen via the proton-proton or pp chain above about 5 MK. The core temperature of the sun is 1.6 MK. In the beginning, the sun had 71% H, 27% He and 2% heavier elements. Now, the amount of H at the core has been reduced to only 36%.
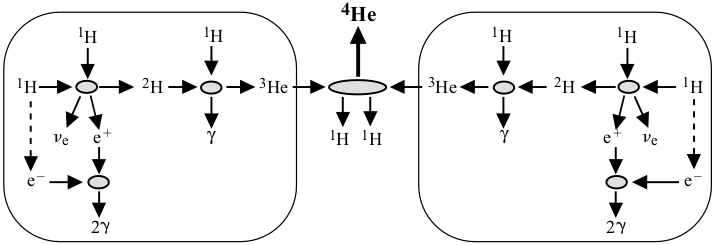
Neutrinos escape from the star. The electron and positron annihilate to create two gamma rays with energy $ E_{2\gamma} \approx 2m_e c^2 = 1.0 $ MeV. This and the motion of the deuterons contribute to the thermal energy of the star. Overall, six protons give rise to a $^4$He nucleus and two protons.
Number of baryons, leptons and charge must be conserved. We started with 6 baryons and end with 6 baryons (4 protons, 2 neutrons). We started with 6 leptons and end with 6 leptons (4 $e^-$ and 2 $\nu_e$). We started with net charge zero as there were exactly 6 protons and 6 electrons. In the end, the net charge is also zero as there are exactly 4 positive protons and 4 negative electrons left.
Conservation of energy must be true as well. In essence 4 HI atoms were converted to 1 HeI atom.

These are the less probable paths that the pp chain can take. The probability of each path is shown. THe pep process can also create deuterons, but contribute to only 0.4% of all $^4$He terminations. But the pep process emit a 1.44 MeV neutrino as opposed to just a 0.42 MeV neutrino of the pp process. Neutrino astronomers can detect the pep neutrino more easily. The highly improbable hep process creates an even higher-energy neutrino of 18 MeV.
The $\nu_e$ (standard model) from the sun is the main resource for neutrino astronomy. But only half of the expected neutrinos have been detected. The other half might have been transformed to other particles en route from the center to the surface of the sun.
5.2 CNO cycle
The CNO cycle also creates a HeI from four HI just like the pp chain, but produces carbon, nitrogen and oxygen along the way. It needs C as an input which can be available in a star due to the previous generations of stars.

Here is the cycle of six reactions. $^{12}$C fuses with $^1$H first producing $^{13}$N and a photon. The nitrogen decays producing a positron and an electron neutrino. This is known as beta decay because electrons were called beta rays as opposed to alpha rays ($^4$He) in the early days of radioactivity studies.
Here $^{12}$C works only as a catalyst.
5.3 Energy production
The atomic masses of H and He are 1.00783 amu and 4.00260 amu, respectively, where 1 amu = $1.66053\times 10^{-27}$ kg. The energy released by a single set of interactions in pp or CNO process
$$ E_r = -\Delta E_{rest} = (4M_H-M_{He})c^2 = 4.29\times 10^{-12} \text{ J} = 26.75 \text{ MeV} $$
which is 0.71% of the rest-mass energy of four H atoms. The per capita energy production
$$ \frac{E_r}{4M_H} = 0.0071 c^2 = 6.4\times 10^{14} \text{ J/kg} $$
or almost 640 TJ/kg. If I had 640 terra-joules of energy available per kg, I would be able to survive 10 ky. I would need only 10 g of mass for my whole life. Only 2% of this energy in the sun is carried away by neutrinos.
Nuclear burning is is 10 million times more efficient than chemical burning.
Only 10% of H is located in the core where temperature high enough for H fusion. Taking into account the 2% loss due to $\nu_e$, the total energy produced by H burning
$$ E_H \approx (0.98 \times 6.4\times 10^{14} \text{ J/kg}) (0.1\times 2\times 10^{30} \text{ kg}) = 1.3\times 10^{44} \text{ J} $$
or almost 1300 tredecillion joules. So the lifetime of the sun
$$ \tau_\odot = \frac{E_H}{L_\odot} $$
which is around 10 Gy. This is much larger than the thermal timescale we found before.
The energy generation rate $\epsilon_{pp}$ is an important quantity that describes the amount of energy produced per kg (W/kg). We know that $\epsilon \propto X^2 (\rho^2/\rho) T^\beta$ where $X$ is the fraction of mass that is H, $\rho$ is the density of the star and $T$ temperature. The order 2 arises because the rate depends on the flux of both the ‘projectile’ and ‘target’ particles. We divide this by $\rho$ to get the energy rate per mass.
$$ \epsilon = \epsilon_0 X^2 \left(\frac{\rho}{10^5 \text{ kg/m}^3}\right) \left(\frac{T}{10^7 \text{ K}}\right)^\beta $$
| Chain/cycle | Temperature where dominant (MK) | $\beta$ factor | Stars where dominant |
|---|---|---|---|
| pp | $5\sim 15$ | 4 | Sun and less massive |
| CNO | $\ge 20$ | 15 | Type A and more massive |
For the sun, $X=0.71$, but it has been reduced to $0.36$ at the center. Put the other values as $\rho=150$ Mg/m$^3$, $T=16$ MK and $\beta=4$ to get $\epsilon_{pp}=2.4$ mW/kg.
At higher temperatures, CNO cycle dominates the pp chain because of its higher sensitivity to temperature: $\epsilon\propto T^{15}$.
6. Limiting luminosity
The luminosity of a star $L\propto M^{\sim 3}$, but the maximum possible luminosity, called the Eddington luminosity, $L_E\propto M$ which sets an upper limit to the mass of a star. If the mass is more than this, the radiation blows away the photosphere.

Assuming the is made of ionized hydrogen, i. e. free protons and electrons, the gravitational force $F_G$ primarily works on the protons and the radiative force $F_{\text{rad}}$ primarily on the electrons. Eddington luminosity is found by equating the two.
For finding the outward radiative force, note that the energy carried by a photon $E=h\nu=pc$ where $p$ is the momentum. The radiation pressure
$$ P_{\text{rad}} = \dfrac{dp}{dt}\frac{1}{A} = \left(\frac{dE}{dt}\frac{1}{A}\right)\frac{1}{c} = \frac{\phi}{c} $$
where $\phi$ is the energy flux in units of W m$^{-2}$. Then the outward radiative force on a single electron
$$ F_{\text{rad,e}} = P_{\text{rad}} \sigma_T = \frac{\phi\sigma_T}{c} = \frac{L}{4\pi r^2} \frac{\sigma_T}{c} $$
because flux at a radius $r$ is $L/(4\pi r^2)$. And the inward gravitational force on a single proton at the same radius
$$ F_{\text{G,p}} = -\frac{GM\mu_em_p}{r^2} $$
where electron molecular weight $\mu_e$ is the number of nucleons (protons and neutrons) per electron. Now condition for the Eddington limit says
$$ F_{\text{G,p}} + F_{\text{rad,e}} = 0 $$
which entails
$$ L_E = \frac{4\pi G M_\odot \mu_e m_p c}{\sigma_T} \frac{M}{M_\odot} = 1.26\times 10^{31}\mu_e \frac{M}{M_\odot} \text{ W} = 3.27\times 10^4 \mu_e\frac{M}{M_\odot} \text{ L}_\odot. $$
Note that the Eddington luminosity is independent of distance from the center and it is 33,000 times greater than solar luminosity for a 1-solar-mass star. So gravity can confine the solar plasma within the sun except for the million-degree hot gas in the corona which propagates throughout the solar system as solar wind.
In order to find the mass limit for a hydrogen burning star note that $L\propto M^{3.2}$ if the pp process is dominant. That means $L=(M/M_\odot)^{3.2} L_\odot$ which we can equate with the above equation to get
$$ M_{\text{max}} = (3.27\times 10^4 \mu_e)^{1/2.2} M_\odot = 113 M_\odot $$
when $\mu_e=1$ or the gas is made of only hydrogen. And the luminosity of such a star will be
$$ L = 113^{3.2} = 3.6\times 10^6 L_\odot $$
or a million times the luminosity of the sun. We have not found a star more than 130 times massive than the sun.
The stars close to their Eddington limit are erratic and called luminous blue variables (LBV). Their brightness changes with periods of months to years. For example, $\eta$ Car and P Cyg have shown outbursts in historical times. The ejections from LBVs are due, in part, to the radiation pressure.
6.1 Mass accretion

The Eddinton luminosity for a 1.4 M$_\odot$ neutron star is around $1.8\times 10^{31}$ W and the maximum luminosity of neutron stars has been observed to be around that. This proves that the emission mechanism of a neutron star is mass falling onto a neutron star from a companion star.
If a star has an accretion rate of $\dot{m}=dm/dt$, then the accretion luminosity
$$ L_{\text{acc}} = \frac{GM \dot{m}}{R} $$
which is associated with the potential energy lost by a mass $dm$ as it infalls from infinity to a radius $R$. We can define an Eddington accretion rate $\dot{m}_E$ by equating the luminosity to $L_E$:
$$ \dot{m}_E \approx 1.26\times 10^{31} \frac{R}{GM_\odot} $$
which does not depend on the mass of the recipient star. For a 10-km neutron star $ \dot{m}_E \approx 10^{15} $ kg/s or $10^{-8}$ M$_\odot$/year.

On the other hand, we have found quasars with luminosity of $10^{39}$ W. Setting this value in the equation of Eddington luminosity we find the mass of the accreting object to be $10^8$ M$_\odot$. As the emission is often variable it must be coming from a small region of light-year size. And only black holes can have 100 million solar masses within a light year. This was the proof that the radiation of quasars is coming from matter falling into a black hole.
The radius of a black hole is around $R=2GM/c^2$ which would be 2 astronomical unit for 100 million solar masses. Putting this value in the accretion rate equation we find that such a black hole gobbles up only half a solar mass per year which is pretty modest.
7. Instability and pulsation
Stars are not totally stable, all stars are subjected to some variability, they all physically oscillate, shrink and expand in a periodic manner. We study the oscillations using atmospheric velocity vectors and brightness in the field rightly called asteroseismology and, in case of the sun, helioseismology.
If the oscillation amplitude is high, we call the stars pulsating variables that include quasi-periodic cepheid variables and RR Lyrae variables which are used to measure the distance of galaxies. Let us deal with the basic thermodynamics controlling these two types of variable stars.

The oscillation of these stars can be explained using the 4-step Carnot cycle used for describing the changes of state of a volume of gas. During the cycle, the gas absorbs heat and does some work on the surroundings. On the P-V plot above, work $W=\int P dV$ is the area under a curve with certain limits. Work is positive for movement to the right (upper path, isothermal expansion), negative for movement to the left (lower path, isothermal compression). The lower path yields lower negative work due to lower pressure compared to the the positive work for the upper path. So the net work is positive, which is always the case for clockwise cycle. If the cycle was counterclockwise, work would be done on the gas, i. e. work would be negative.
In a star, the heat $Q$ is provided by radiant energy of the hot gas and the work results in a physical expansion and compression of the whole star, and the internal energy $U$ does not change.
First law of thermodynamics states the law of energy conservation for a reversible process:
$$ \delta Q = dU + \delta W $$
where the $d$ and $\delta$ make it clear that $U$ is a state variable (internal property of a system) while $Q$ and $W$ are not. Pressure $P$, volume $V$, temperature $T$ and entropy $S$ are also state variables. $\delta Q$ is positive when gas absorbs heat, $\delta W$ is positive when gas works on the surroundings. Over a complete cycle, the loop integral
$$ \oint dU = 0 \Rightarrow W = + \oint \delta Q $$
where the positive sign makes it explicit that pulsations occur only if work is positive. Because entropy is a state variable its integral over the cycle must be zero as well:
$$ \oint dS = \oint \frac{\delta Q}{T} = 0. $$
Now, the variation of temperature can be approximated as a small fluctuation $\Delta T(t)$ in time over an average temperature $T_0$:
$$ T(t) = T_0 + \Delta T(t) = T_0\left(1+\frac{\Delta T(t)}{T_0}\right). $$
Assuming $\Delta T / T \ll 1$ we can approximate via an expansion that
$$ \frac{1}{T} = \frac{1}{T_0} \left(1+\frac{\Delta T}{T_0}\right)^{-1} = \frac{1}{T_0} \left(1-\frac{\Delta T}{T_0}\right) $$
which can be plugged in the equation of entropy to get
$$ W = \oint \delta Q \approx \oint \frac{\Delta T(t)}{T_0} \delta Q $$
which means $W$ and $\Delta T$ have the same sign, heat is absorbed (work on the surrounding) when temperature increases and discharged (work on the gas) when temperature decreases. This is similar to a heat engine, for example, an internal combustion engine. In both cases, heat is introduced during an expansion at high temperature ($T_2$) and dumped during a compression at low temperature ($T_1$).
The ultimate condition for pulsation is achieved when we integrate the above equation over the whole mass of the star:
$$ W \approx \int_M \oint_Q \frac{\Delta T(t,m)}{T_0(m)} \delta Q(m) \ dm > 0. $$
In a heat engine, the operative mechanism is the burning of fuel. In a star, the operative mechanism is the valving of heat by the changing opacity in a star’s ionization transition zone as shown below.

Inward of the transition zone gas is hot and ionized, outward the gas is cold and neutral. For H and He, the transition zone is close to the surface. The transition zone itself is a mix of hot and cold gas.
(a) When a star compresses (due to a breakdown of equilibrium), temperature in the transition zone increases leading to more ionization. The number of free electrons increases leading to a higher opacity, meaning obstruction to photons. Photons are trapped by the free electrons via scattering. The trapped outward radiation provides heat which is absorbed at a high temperature a required by a heat engine.
(b) The trapped heat causes the star to expand and cool. This leads to recombination for many atoms, so ionization and number of free electrons decrease. The highway of photons is open again and the photons carry away the trapped heat. Heat is released at a low temperature.
Due to higher volume and lower temperature, pressure decreases ($P \propto T/V$) and the outer layers of the star collapse due to self-gravity leading to a compression which takes us back to (a).
RR Lyrae and Cepheid variables can be used to measure large distance because they are very luminous (300 to 30,000 times higher than the sun) and their luminosity is related to their period.