Table of Contents
IX. Electromagnetic induction
1. Faraday's law
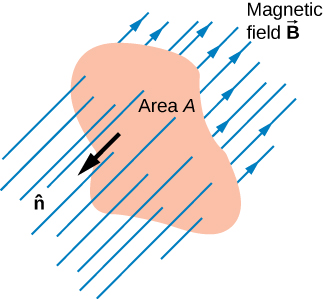
Magnetic flux is defined as
$$ \Phi_m = \int_S \vec{B} \cdot d\vec{A} = \int_S \vec{B} \cdot \hat{n} dA $$
where $\hat{n}$ is the normal vector to the area $\vec{A}$. Unit is weber, Wb. 1 Wb = 1 T m$^2$.
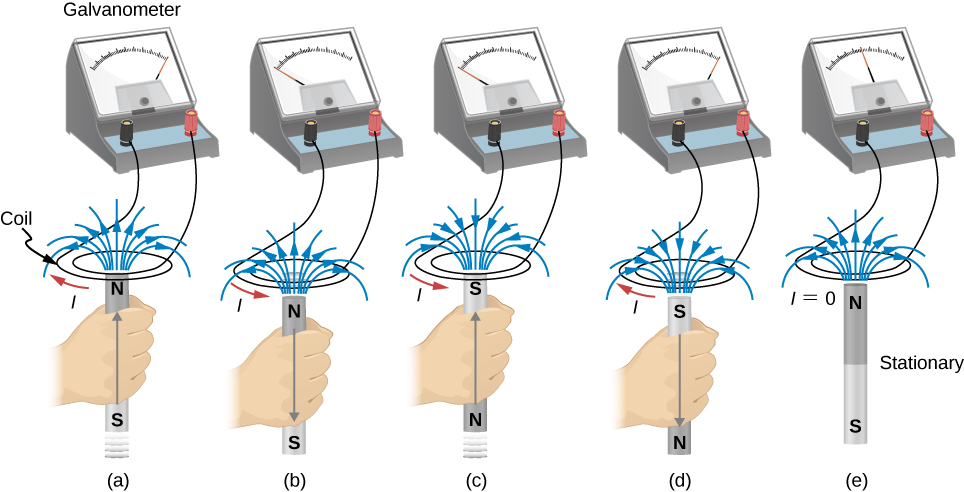
Michael Faraday observed the following phenomena.
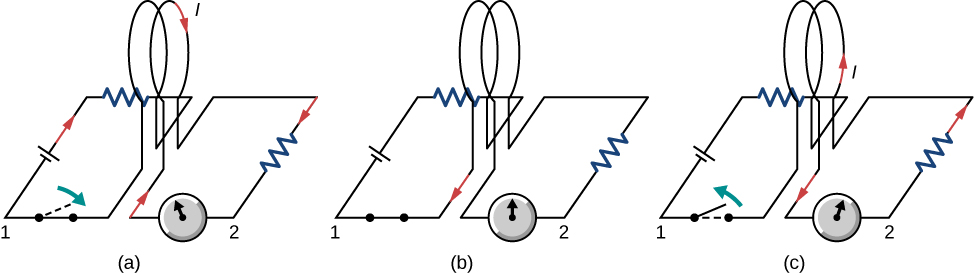
Faraday’s law says that the induced emf (electromotive force, voltage) in a circuit
$$ \varepsilon = -\frac{d\Phi_m}{dt} $$
that is the emf is the negative of the rate of change of the magnetic flux through the circuit.
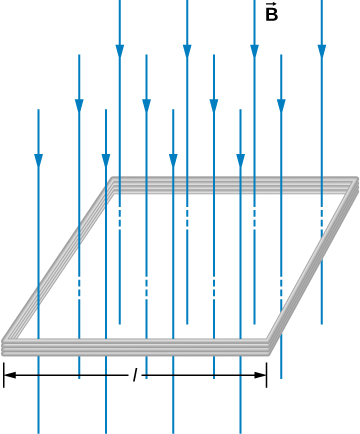
If there are multiple turns like above then
$$ \varepsilon = -N \frac{d\Phi_m}{dt}. $$
2. Lenz's law
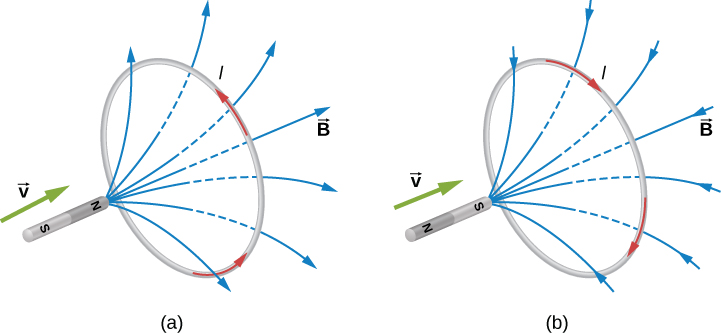
The direction of the induced emf drives current around a wire loop to always oppose the change in magnetic flux that causes the emf.
3. Motional emf
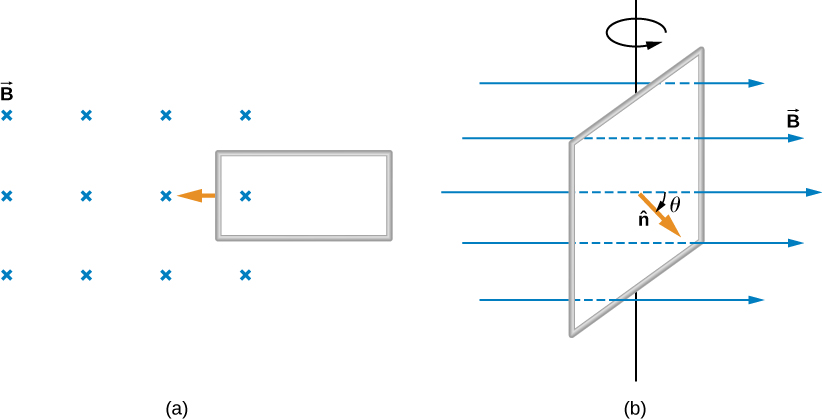
Magnetic flux varies with field, area and the angle between field and area. Variation of any one of these will induce an emf.
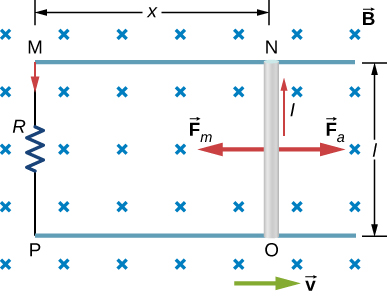
The area of MNOP $A=lx$ and the flux $\Phi=BA=Blx$. The induced emf
$$ \varepsilon = -\frac{d\Phi}{dt} = Bl\frac{dx}{dt} = Blv $$
and the current induced in the circuit
$$ I = \frac{\varepsilon}{R} = \frac{Blv}{R}. $$
From the energy point of view, $\vec{F}_a$ produces power $P=F_a v$:
$$ F_a v = IlBv = \frac{Blv}{R} Blv = \frac{l^2 B^2 v^2}{R}. $$
The power dissipated
$$ P = I^2 R = \frac{l^2 B^2 v^2}{R}. $$
The produced and dissipated power are equal.
4. Induced electric field
Faraday’s law can rewritten in terms of the induced electric field.
$$ \varepsilon = \oint \vec{E} \cdot d\vec{l} = - \frac{d\Phi_m}{dt}. $$
Note that for the electrostatic case $\oint \vec{E} \cdot d\vec{l}=0$.
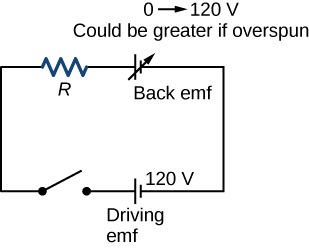
5. Electric generators and back emf
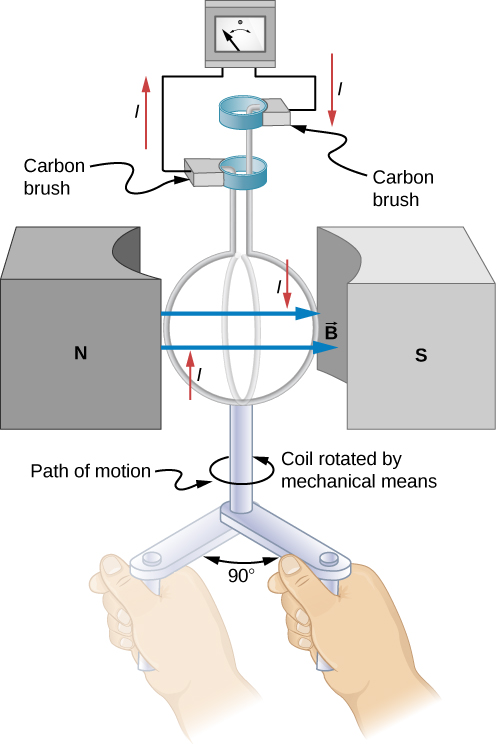
Calculate the emf induced when the call is rotated from $\theta=0^\circ$ to $90^\circ$:
$$ \varepsilon = -\frac{d\Phi}{dt} = NBA \sin\theta \frac{d\theta}{dt}. $$
Here $A=\pi r^2$, $N=200$, $r=5$ cm, $B=0.8$ T, $d\theta=\pi/2$ and $dt=15$ ms.
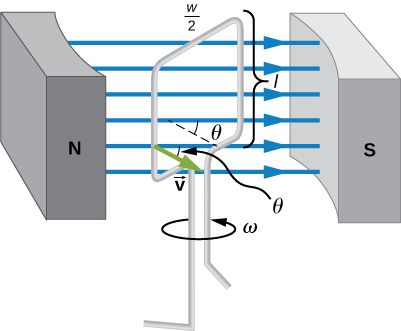
In the above diagram, emf is produced on both side of the loop, total emf
$$ \varepsilon = 2Blv\sin\theta = 2Blv\sin(\omega t) $$
where $\omega$ is the angular velocity. So $v=r\omega$ and $r=w/2$ if $w$ is the width of the loop. So
$$ \varepsilon = 2Bl \frac{w}{2}\omega \sin(\omega t) = (lw)B\omega \sin(\omega t) = AB\omega \sin(\omega t). $$
If there are $N$ loops just multiply by $N$. We can write
$$ \varepsilon = \varepsilon_0 \sin(\omega t) $$
where $\varepsilon_0 = NBA\omega$ as you see below.
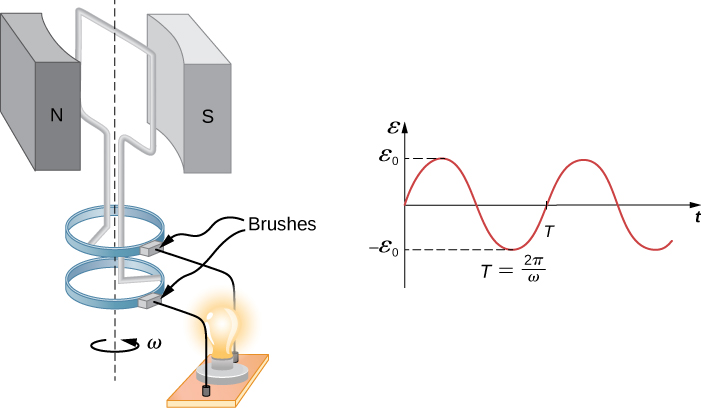
The frequency of the oscillation of this alternating current is $f=\omega/(2\pi)$ and the period $T=2\pi/omega$.