Table of Contents
VIII. Sources of magnetic field
1. The Biot-Savart law
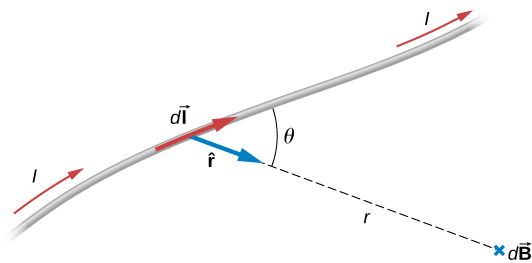
This is an empirical law. The magnetic field produced by a current
$$ d\vec{B} = \frac{\mu_0}{4\pi} \frac{I d\vec{l}\times \hat{r}}{r^2} $$
where the vacuum permeability $\mu_0=4\pi\times 10^{-7}$ T m A$^{-1}$.
The direction of $d\vec{B}$ can be found using the right hand rule. So magnetic field
$$ \vec{B} = \frac{\mu_0}{4\pi} \int_{wire} \frac{I d\vec{l}\times \hat{r}}{r^2}. $$
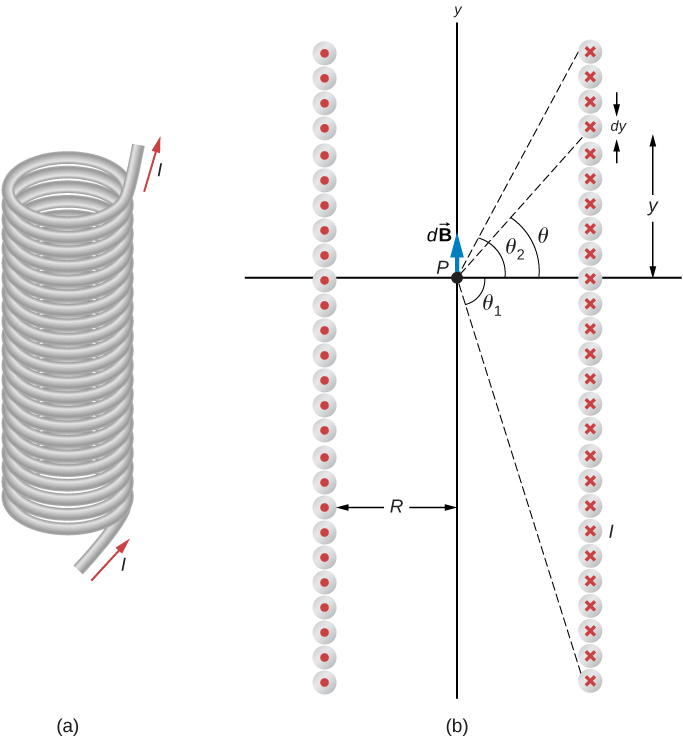
2. Magnetic field due to a thin straight wire
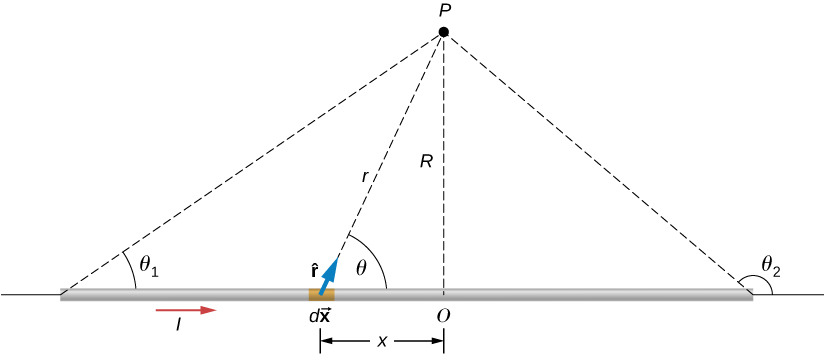
$$ B = \frac{\mu_0}{4\pi} \int_{wire} \frac{I \sin\theta dx}{r^2} $$
Substitute $r^2 = x^2+R^2$ and $\sin\theta = R(x^2+R^2)^{-1/2}$ and evaluate the integral to get
$$ B = \frac{\mu_0 I}{2\pi R} \left[ \frac{x}{(x^2+R^2)^{1/2}} \right]_{wire} $$
and if the wire is infinite, limit is from $0$ to $\infty$ and we get
$$ B = \frac{\mu_0 I}{2\pi R}. $$
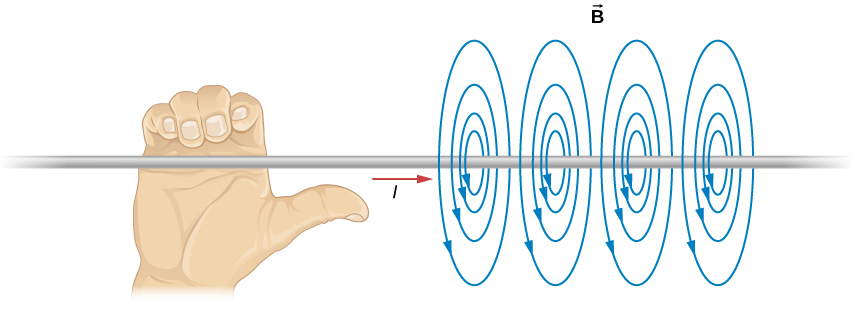
There is a circular symmetry, magnetic field lines are circular around a current carrying wire and the field decreases by a factor equal to the circumference.
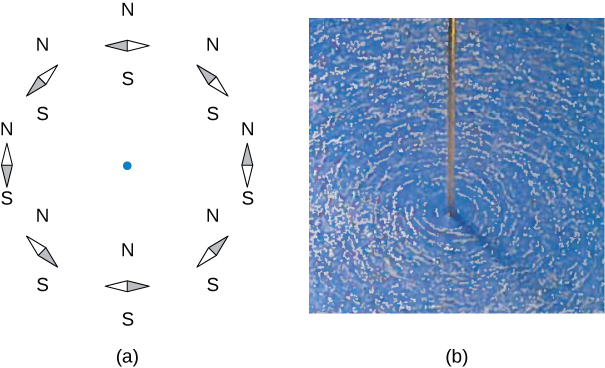
Magnetic field lines can be visualized using compass needles or iron feelings.
3. Magnetic force between parallel conductors
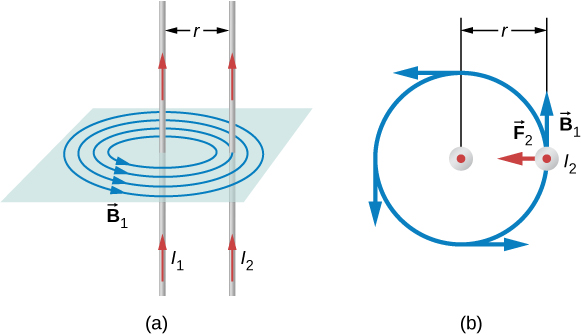
The magnetic field for the first wire,
$$ B_1 = \frac{\mu_0 I}{2\pi r} $$
Because of this the first wire exerts a force $F_2$ on the second wire and this force
$$ F_2 = I_2 l B_1 \sin\theta = I_2 l B_1 $$
and the force per unit length becomes
$$ \frac{F}{l} = \frac{\mu_0 I_1 I_2}{2\pi r} $$
where $r$ is the distance between the wires. It is attractive if current is in the same direction, and repulsive for opposite currents.
4. Magnetic field of a current loop
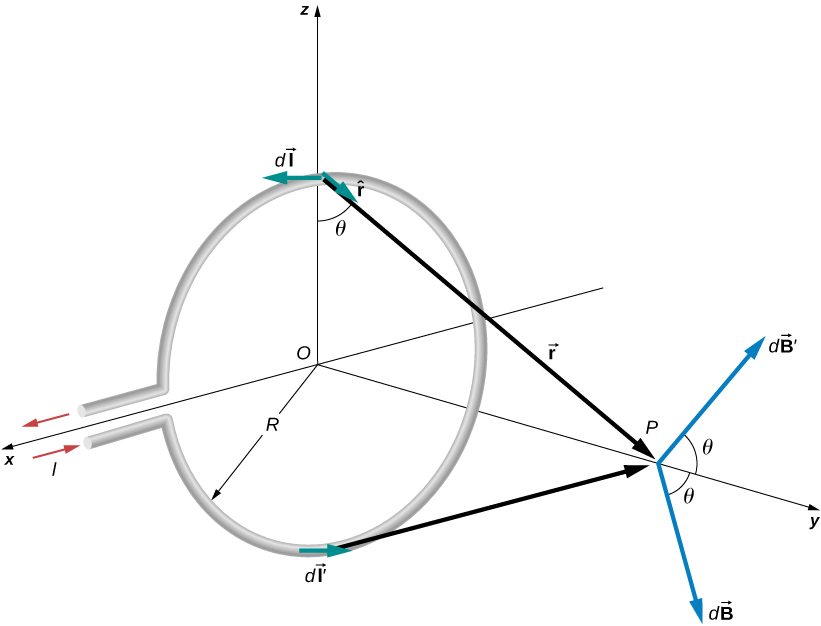
Magnetic fields only along the $y$ axis do not cancel out. So
$$ \vec{B} = \hat{j} \int_{loop} dB \cos\theta = \hat{j} \frac{\mu_0 I}{4\pi} \int_{loop} \frac{\cos\theta dl}{y^2+R^2} $$
where $\cos\theta = R(y^2+R^2)^{-1/2}$. Putting this in the equation and evaluating the integral we get
$$ \vec{B} = \frac{\mu_0 I R^2}{2 (y^2+R^2)^{3/2}}\hat{j} $$
and by setting $y=0$ we get the final form
$$ \vec{B} = \frac{\mu_0 I}{2R} \hat{j} $$
Task: express this in terms of magnetic dipole moment $\vec{\mu} = IA \hat{n}$.
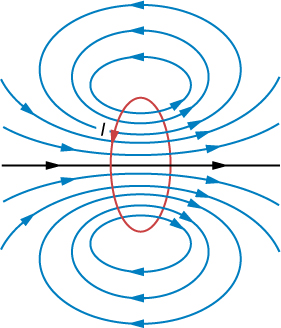
$$ \frac{\mu_0 \vec{\mu}}{2\pi y^3} $$
5. Ampère's law
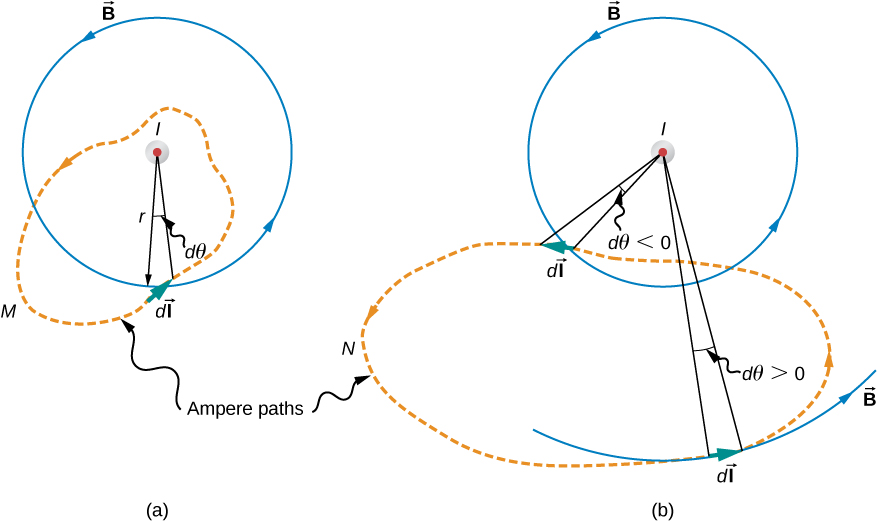
For the M path $\int \vec{B} \cdot d\vec{l} = Br d\theta = \mu_0 I$.
Over the N path $\int \vec{B} \cdot d\vec{l} = 0.$
Ampere’s law states
$$ \oint \vec{B} \cdot d\vec{l} = \oint \frac{\mu_0 I}{2\pi r} r d\theta = \mu_0 I. $$
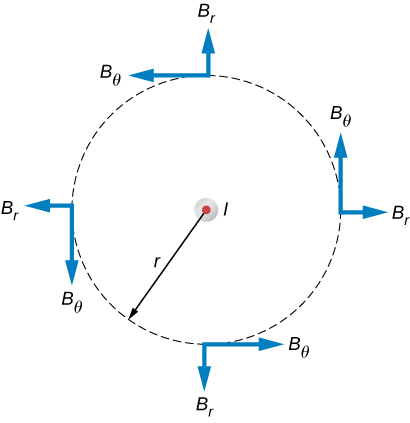
Calculate magnetic field due to an infinitely long thin wire straight wire.
6. Solenoids and toroids
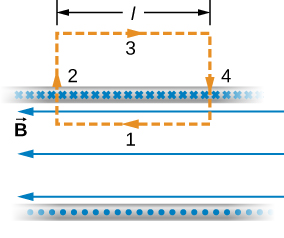
Magnetic field outside the solenoid is zero and inside $B=\mu_0 n I$ where is $n$ is the number of turns.
A magnetic resonance imaging (MRI) machine.
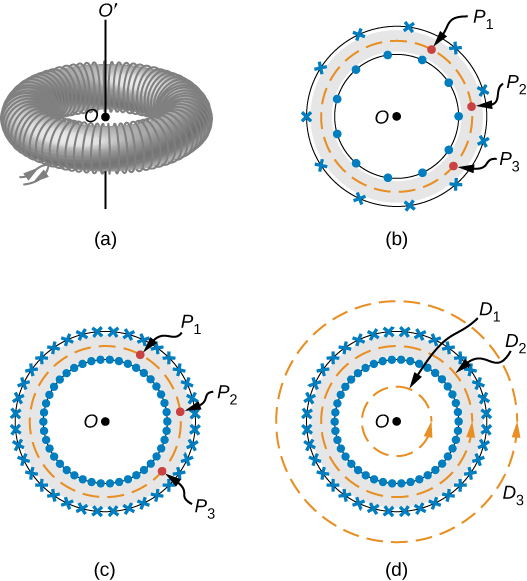
For paths $D_1$ and $D_2$, no net current passes through the surface. For path $D_2$
$$ \oint \vec{B} \cdot d\vec{l} = \mu_0 N I \Rightarrow B = \frac{\mu_0 NI}{2\pi r}. $$
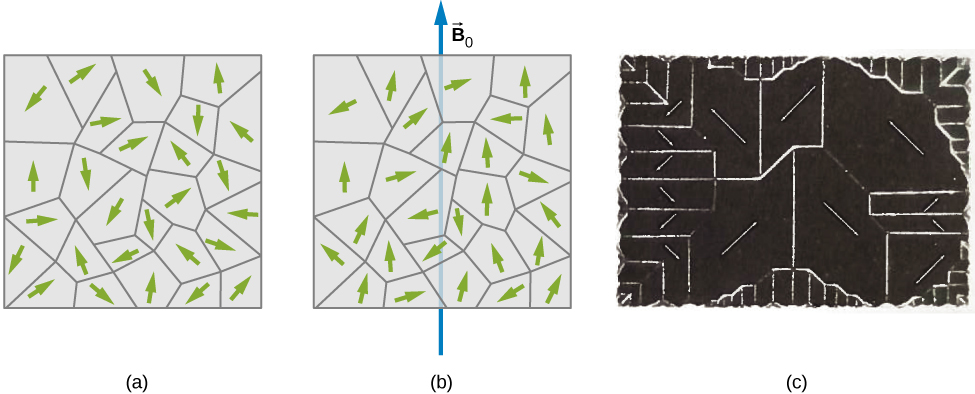
7. Magnetism in matter
7.1 Paramagnetic material
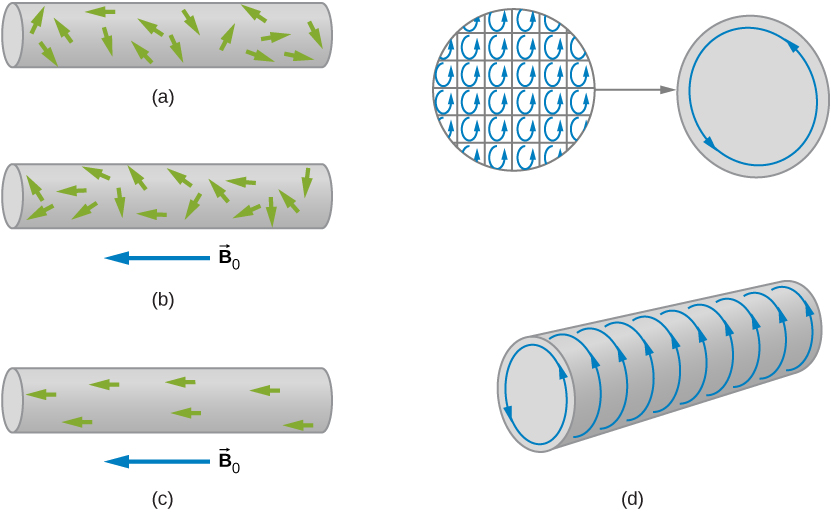
$$ \vec{B} = \vec{B}_0 + \vec{B}_m = \vec{B}_0 + \chi \vec{B}_0 = (1+\chi)\vec{B}_0 $$
where $\chi$ is a dimensionless quantity called magnetic susceptibility. The magnitude of the magnetic field
$$ B = (1+\chi)\mu_0 nI = \mu nI $$
where the magnetic permeability of a material
$$ \mu = (1+\chi)\mu_0 $$
where $\mu_0$ is the magnetic permeability of free space.
For paramagnetic material $\chi$ is positive and it is negative for dimagnetic material.
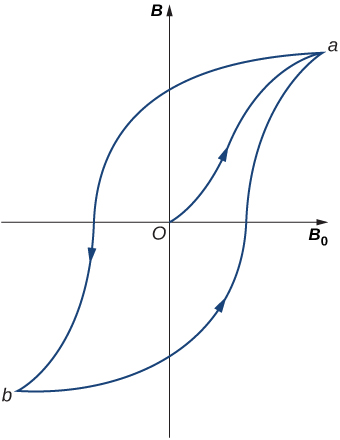
7.2 Ferromagnetic material