III. Electric potential

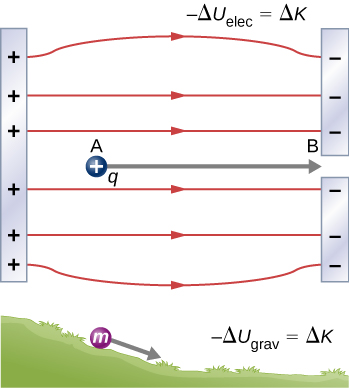
Charge accelerated by electric field is analogous to mass accelerated by gravitational field. In both cases, potential energy is converted to kinetic energy and the work $W=\Delta K=-\Delta U$ according to the work-energy theorem. Potential energy is easier to calculate than work.

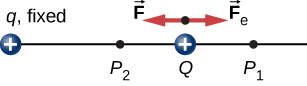
Charge q is fixed and Q is moved toward q by applying an external force $\vec{F}$ which is exactly equal to the electric force $\vec{F}_e$ at each position. So work for bringing it to $P_2$ from $P_1$

$$ W_{12} = \int_{P_1}^{P_2} \vec{F} \cdot d\vec{r} $$

If we define Coulomb constant $k=1/(4\pi\epsilon_0)=9\times 10^9$ N m$^2$ C$^{-2}$, then this external force

$$ \vec{F} = \vec{F}_e = \frac{kqQ}{r^2} \hat{r} $$

and the distance from origin to $P_1$ and $P_2$ as $r_1$ and $r_2$, then work

$$ W_{12} = kqQ \int_{r_1}^{r_2} \frac{1}{r^2} \hat{r} \cdot \hat{r} dr = kqQ \left[-\frac{1}{r}\right]_{r_1}^{r_2} = -kqQ \left(\frac{1}{r_2}-\frac{1}{r_1}\right). $$

This would also be true in a polar coordinate system with q at center at Q at a distance r. The work is independent of the path taken and only depends on the endpoints, because electric force is conservative.

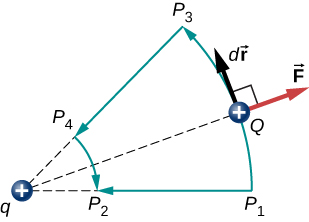
Imagine two paths for Q to go from $P_1$ to $P_2$, one direct, the other via $P_3$ and $P_4$. Work is zero along $P_1P_3$ and $P_4P_2$ because $\vec{F}$ and $d\vec{r}$ are perpendicular. So along $P_1P_3P_4P_2$, the only work is done while the charge moves along $P_3P_4$ which is equal to the work done along $P_1P_2$.

If the charge travels along $P_1P_3P_4P_2P_1$ and comes back to its original position, the net work is zero. Because force $\vec{F}=q\vec{E}$, electric field is also conservative, i. e.

$$ \oint = \vec{E} \cdot d\vec{r} = 0. $$

Now we can define electric potential energy difference ($\Delta U$) using work. The work done while bringing a charge from a reference position $r_0$ to $r$

\begin{equation} W = \int_{r_0}^r \vec{F} \cdot d\vec{r} = -\Delta U \\ \Rightarrow \Delta U = -kqQ \left[-\frac{1}{r}\right]_{r_0}^r = kqQ \left(\frac{1}{r}-\frac{1}{r_0}\right) = U(r) - U_0 \\ \Rightarrow U(r) = \frac{kqQ}{r} - U_0. \end{equation}

A convenient reference is at $r=\infty$ where $U_0=U(\infty)=0$ and hence the potential energy is simply

$$ U(r) = \frac{kqQ}{r} $$

just as gravitational potential energy $U_g(r)=-GmM/r$.

Potential energy is positive if the charges are of same type and negative if the charges are opposite. If you bring two positive charges together, you have to do some work on the system thereby increasing the potential energy of the system, this is why $U$ is positive in this case. Two opposite charges on the other hand will come closer by themselves thereby decreasing the potential energy of the system. This is why, $U_g$ is also negative as the force is attractive.

If there are many charges in a system, you can create $ij$ pairs, calculate $U_{ij}$ for each pair and sum all the energies to get the total potential energy of the system as

$$ U = \frac{1}{2} k \sum_{i}^{M} \sum_{j}^{N} \frac{q_iq_j}{r_{ij}} \text{ for } i \ne j. $$

Potential energy is scalar like work, so the addition is much more convenient than force or field.

Electric force depends on two charges, a source charge and a test charge, but electric field only depends on the source charge. Similarly, it is convenient to define a quantity from the potential energy that will be independent of the test charge. Electric potential energy of $U$, but the electric potential

$$ V = \frac{U}{q} \text{ or } \Delta V = \frac{\Delta U}{q}. $$

where $q$ is the test charge. So electric potential is the potential energy per unit charge. This is also called potential difference, but the most familiar name is voltage. The unit obviously would be J/C (joule per coulomb) or V (volt).

Voltage ($V$) and energy ($U$)are not the same thing. Voltage is energy per unit charge. So a motorcycle battery and a car battery can have the same voltage (e. g. 12 V) even though the car battery can store much more energy than that of the motorcycle.

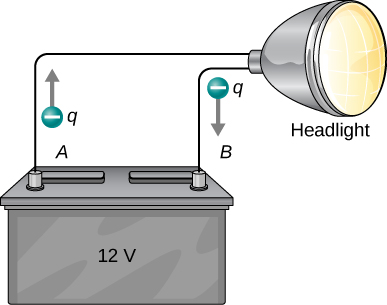
A battery repels negative charges (electrons) from its negative terminal and attracts them toward its positive terminal, so electrons move from positive to negative terminals as shown above. The potential difference or voltage $\Delta V = V_B - V_A = +12$ V which is positive. But as the charge $q$ is negative, the energy $\Delta U=q\Delta V$ is negative. When $q$ moves from A to B, $U$ decreases, so $\Delta U=U_B-U_A$ is negative.

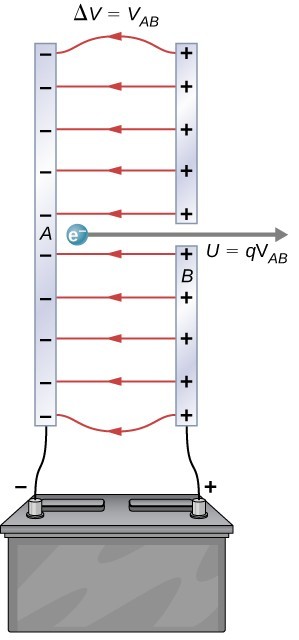
In the figure above, it is more convenient to use eV (electron-volt) as the unit of energy. An electron is accelerated from the negative to the positive plate by converting potential energy into kinetic energy. If the potential difference between the plates is 1 V, the energy gained by electrons is exactly 1 eV. The unit is created by the fact that $U=qV$, when $q=e$ and $V=1$ V, $U=1$ eV.

$$ 1 \text{ eV} = (1.6\times 10^{-19} \text{ C})(1 \text{ J/C}) = 1.6\times 10^{-19} \text{ J}. $$

Note that conservation of energy holds true here as well: $K+U=$ constant, or $\Delta K+\Delta U=0$.

Voltage is an integral of electric field over some path length. To derive this, start from the potential energy difference $U(r)$ with respect to a reference $U(r_0)$

$$ U(r) = - \int_{r_0}^r \vec{F} \cdot d\vec{r} = -q \int_{r_0}^r \vec{E} \cdot d\vec{r} $$

and then use the relation $V=U/q$ to get

$$ V(r) = \int_{r_0}^r \vec{E} \cdot d\vec{r}. $$

Consider the case when $r_0=\infty$ and we are calculating the potential at a distance $r$ from a point charge $q$:

$$ V_r = \int_{\infty}^r \frac{kq}{r'^2} \hat{r} \cdot \hat{r} dr' = \left[\frac{kq}{r'}\right]_{\infty}^r = \frac{kq}{r}. $$

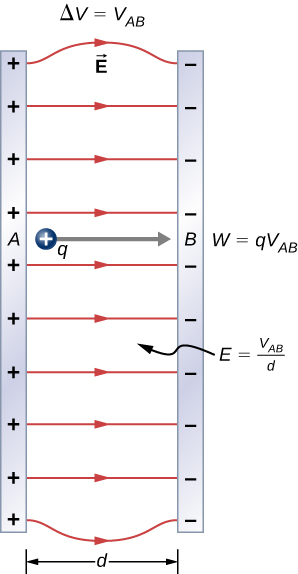
Work needed to move point charge $q$ a distance $d$ from positive higher potential terminal to the negative lower potential terminal $W=\Delta U = -q\Delta V$. The potential difference between the points

$$ V_{AB}=-\Delta V = -(V_B-V_A) = V_A-V_B. $$

Therefore, work $W=qV_{AB}$. But work $W=\vec{F}\cdot\vec{d}=Fd=qEd$. Combining with the previous equation, we get

$$ qEd = qV_{AB} \Rightarrow V_{AB} = Ed \Rightarrow E = \frac{V_{AB}}{d} $$

which is valid for uniform electric field only. It implies another unit of electric field if V/m (volt per meter). 1 N/C = 1 V/m. And in integral form we can write

$$ V_{BA} = V_B-V_A = -\int_A^B \vec{E}\cdot d\vec{l}. $$

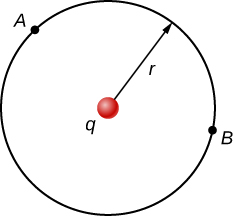
What is the potential difference between A and B? Here $d\vec{l}=r\hat{\theta}d\theta$ and $\vec{E}=kq\hat{r}/r^2$ and, therefore

$$ V_{BA} = -\int_A^B \frac{kq}{r^2} \hat{r} \cdot \hat{\theta} r d\theta = 0 $$

because $\hat{r}\cdot\hat{\theta}=0$. For a point charge at the center, there is no potential difference between points at a constant radius.

For a point charge we already know the potential $V=kq/r$. Potential at infinity is zero. So potential decreases with distance from the charge and becomes zero at infinity. For multiple point charges we can calculate the potential at a point $P$ as

$$ V_P = k \sum_{i=1}^N \frac{q_i}{r_i} $$

where $r_i$ is the distance of the charge $q_i$ from the point $P$ and $k$ is Coulomb constant. For a continuous distribution of charges

$$ V_P = k \int \frac{dq}{r} \text{ where } dq = \begin{cases} \lambda \ dl\ \text{ in one dimension} \\ \sigma \ dA \ \text{ in two dimensions} \\ \rho \ dV \ \text{ in three dimensions}. \end{cases} $$

Calculate potential at point $P$ due to this dipole.

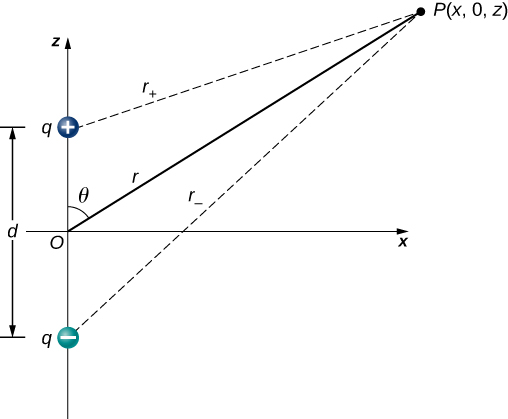
$$ V_P = V_+ + V_- = k\left(\frac{q}{r_+}-\frac{q}{r_-}\right) \text{ and } r_\pm = \sqrt{x^2+\left(z\mp \frac{d}{2}\right)} $$

In polar coordinates, $x=r\sin\theta$ and $z=r\cos\theta$. Replace this and do some algebraic acrobatics to find

$$ \frac{1}{r_\pm} = \frac{1}{r}\left(1\pm \frac{d\cos\theta}{2r}\right) $$

and then substitute this into the equation of potential to get

$$ V_P = k\frac{qd\cos\theta}{r^2}. $$

If we define electric dipole moment $\vec{p} = q\vec{d}$ we can finally write

$$ V_P = k\frac{\vec{p}\cdot\hat{r}}{r^2}. $$

This is the dipole potential in terms of the dipole moment. There higher order moments like quadrupoles, octupoles, etc.

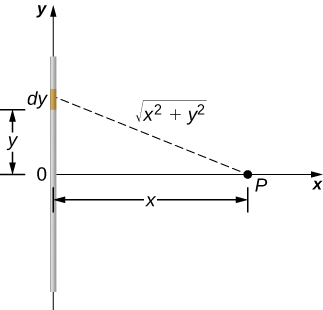
$$ V_P = k\int\frac{dq}{r} = k \int_{-L/2}^{L/2} \frac{\lambda dy}{\sqrt{x^2+y^2}} $$

Carry out the integration and find the following

$$ V_P = k\lambda \ \ln\left[\frac{L+\sqrt{L^2+4x^2}}{-L+\sqrt{L^2+4x^2}}\right]. $$

If $x\rightarrow \infty$, the terms inside the logarithm approaches 1, and the logarithm approaches 0. So the potential at infinity for a finite charge is zero, as expected.

The previous result cannot be used because $L\rightarrow\infty$ is meaningless.

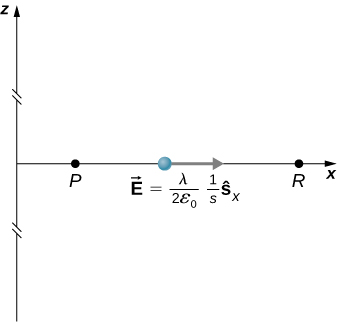
So integrate over the electric field to find potential.

$$ V_P = -\int \vec{E}\cdot d\vec{s} = -\int \frac{2k\lambda}{s} ds = -2k\lambda \ \ln\frac{s_P}{s_R} $$

and if reference potential $V_R=0$ at $s_R=1$ m, then

$$ V_P = -2k\lambda \ \ln s_P. $$

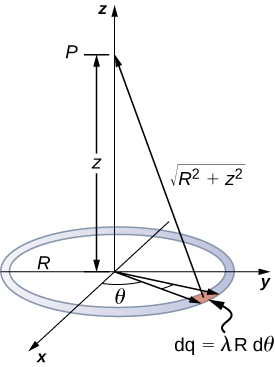
$$ V_P = k\int\frac{dq}{r} = k\int_0^{2\pi} \frac{\lambda R d\theta}{\sqrt{z^2+R^2}} = \frac{k\lambda 2\pi R}{\sqrt{z^2+R^2}} = k\frac{q_t}{\sqrt{z^2+R^2}}. $$

Note the similarity between this equation and the general equation of potential.

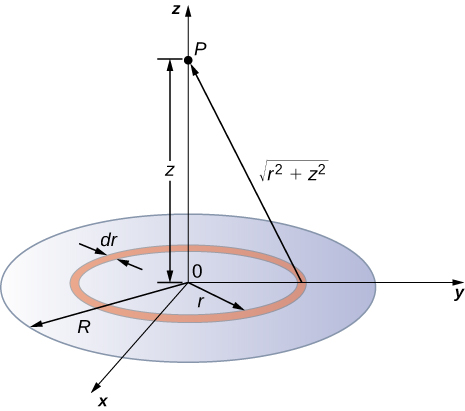
$$ V_P = k\int\frac{dq}{\sqrt{z^2+r^2}} = 2\pi k\sigma\int\frac{rdr}{\sqrt{z^2+r^2}} = 2\pi k\sigma(\sqrt{z^2+R^2}-z). $$

For uniform electric field $E=-\Delta V/\Delta s$, so electric field is the gradient (grade or slope) of potential.

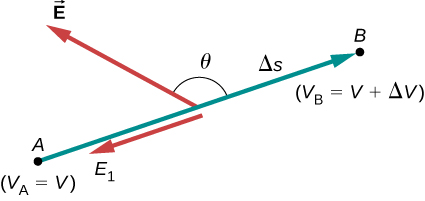
But for a general case, the electric field component along the distance $s$,

$$ E_s = -\frac{dV}{ds} = -\left(\frac{\partial V}{\partial x}+\frac{\partial V}{\partial y}+\frac{\partial V}{\partial z}\right). $$

If we define the gradient using the ‘del’ or ‘grad’ operator

$$ \vec{\nabla} = \hat{i}\frac{\partial}{\partial x}+\hat{j}\frac{\partial}{\partial y}+\hat{k}\frac{\partial}{\partial z} $$

then the field can be rewritten as

$$ \vec{E} = -\vec{\nabla}V. $$

Note that for the cylindrical and spherical symmetries, the del operator becomes

$$ \vec{\nabla}_c = \hat{r}\frac{\partial}{\partial r}+\hat{\phi}\frac{1}{r}\frac{\partial}{\partial \phi}+\hat{z}\frac{\partial}{\partial z} \text{ and} $$

$$ \vec{\nabla}_s = \hat{r}\frac{\partial}{\partial r}+\hat{\theta}\frac{1}{r}\frac{\partial}{\partial \theta}+\hat{\phi}\frac{1}{r\sin\theta}\frac{\partial}{\partial \phi}. $$

The potential $V=kq/r$ and the symmetry is spherical. So electric field

$$ \vec{E} = -\left(\hat{r}\frac{\partial}{\partial r}+\hat{\theta}\frac{1}{r}\frac{\partial}{\partial \theta}+\hat{\phi}\frac{1}{r\sin\theta}\frac{\partial}{\partial \phi}\right) \frac{kq}{r} = -kq\left(\hat{r}\frac{\partial}{\partial r}\frac{1}{r}\right) = k\frac{q}{r^2}\hat{r}. $$

Here the potential $V=kq_t/\sqrt{z^2+R^2}$, so the partial differentiation should be only along the $z$-axis and hence the electric field

$$ E=E_z=-\frac{\partial}{\partial z} \frac{kq_t}{\sqrt{z^2+R^2}} = k\frac{q_t z}{(z^2+R^2)^{3/2}}. $$

The lines along which potential is always same are called equipotential lines and the surfaces on which the potential is always same are the equipotential surfaces.

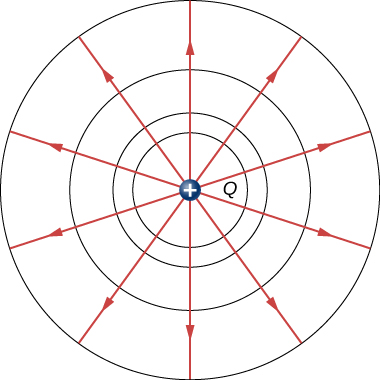
Each circle surrounding this point charge $Q$ is a equipotential line. If you imagine spherical surfaces concentric with the charge, then each of those surfaces would be an equipotential surface because remember potential for a point charge $V=kq/r$.

Electric field lines are always perpendicular to equipotential lines or surfaces.

No work is required to move a charge along an equipotential line or surface because potential difference $\Delta V=0$ and, hence, $W=-\Delta U=-q\Delta V=0$.

This fact can also be established using the electric field: $W=\vec{F}\cdot \vec{d}=q\vec{E}\cdot\vec{d}=0$.

The surface of a conductor in static conditions is an equipotential surface. If there was a potential difference, charges would flow. This fact is utilized in grounding or earthing a conductor.

A conductor can replace any equipotential surface. A spherical conductor can replace a point charge.

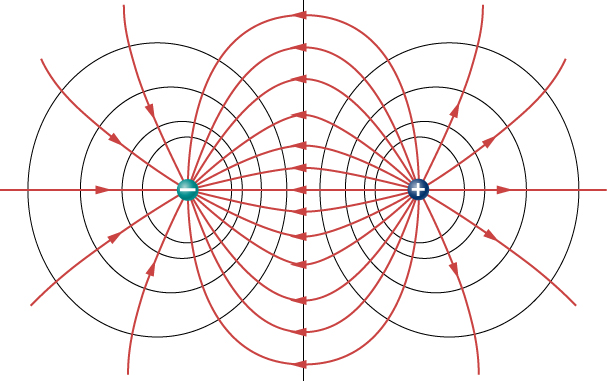
Here you see the electric field lines and equipotential lines for a dipole. One can be drawn using the other. Use the following simulation to visualize fields and equipotentials.