II. Gauss's law

Electric flux for a uniform electric field passing through a flat surface

$$ \Phi = \vec{E} \cdot \vec{A} = \vec{E} \cdot \hat{n} A = EA\cos\theta $$

where $\vec{E}$ is the electric field passing through an area $\vec{A}$ and $\hat{n}$ is a unit vector normal to the surface with area A. Unit of electric flux is obviously N m$^2$ C$^{-1}$ because unit of electric field is N C$^{-1}$ (newton per coulomb).

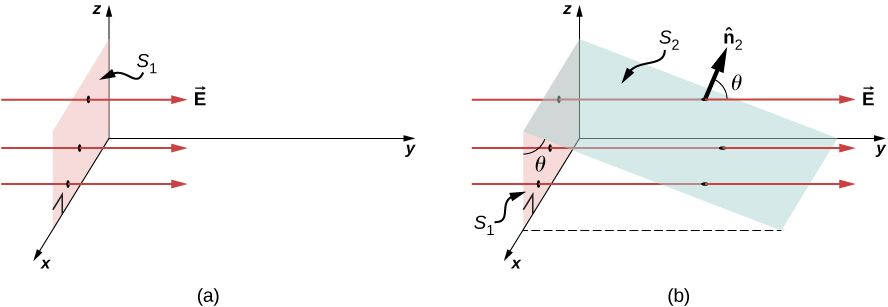
Two cases are shown above. (a) field is perpendicular to the planar surface $S_1$, (b) field is at an angle $\theta$ with surface $S_2$ whose projection onto the xz-plane is $S_1$.

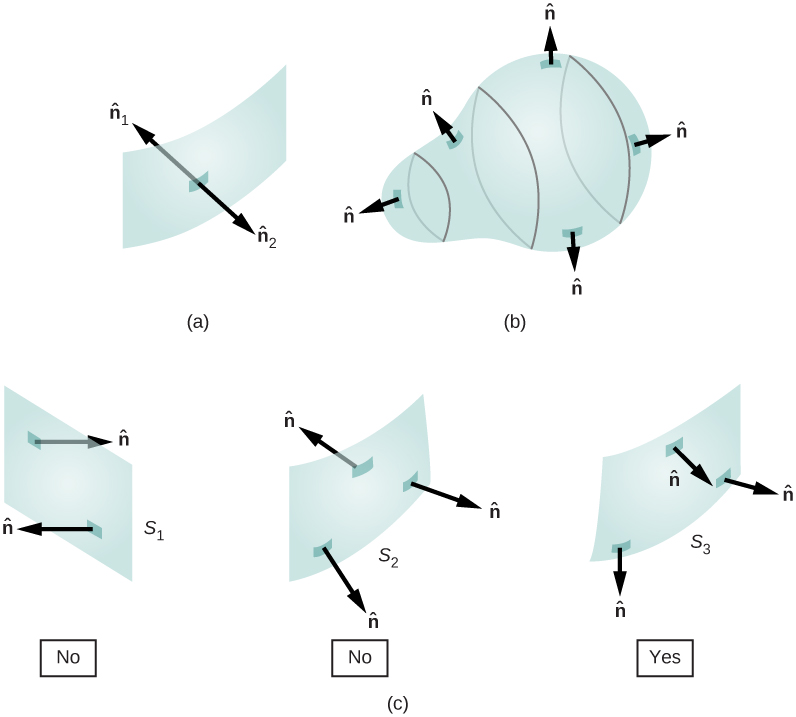
Several area vectors are shown above for open (bottom left) and closed (all other panels) surfaces. For an open surface, $\hat{n}$ any of the two (left or right) directions can be chosen and used consistently. For closed surface $\hat{n}$ is always outward and, hence, called outward normal.

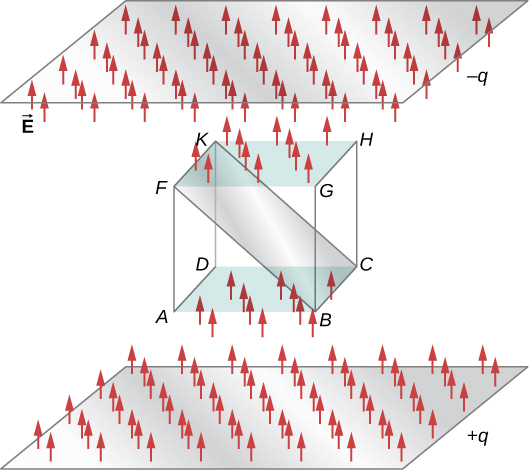
Electric flux through a cube placed between two oppositely charged plates. Flux through ABCD face is negative ($\vec{E}$ and $vec{A}$ in the opposite direction) and FGHK is positive ($\vec{E}$ and $vec{A}$ in the same direction). Field through all other faces is zero. Net flux through the cube is zero. The magnitude of flux through BCKF rectangle is equal to the magnitudes through the top and bottom faces.

Now, what if the the field is not uniform and the area is not flat (as shown below)?

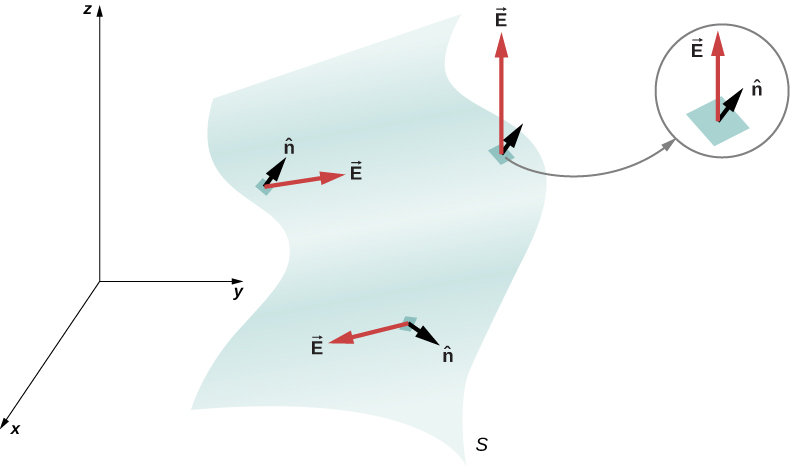
No matter, divide the curved surface into many infinitesimally small flat surfaces, assume the field to be uniform through each of these tiny surfaces, and integrate over the whole surface. If the surface is open electric flux

$$ \Phi = \int_S \vec{E} \cdot \hat{n} dA = \int_S \vec{E} \cdot d\vec{A} $$

and if the surface is closed, electric flux

$$ \Phi = \oint_S \vec{E} \cdot \hat{n} dA = \oint_S \vec{E} \cdot d\vec{A}. $$

If there is no net charge within a closed surface, the number of field lines coming into the surface must be equal to the number of those going out and the net flux through the surface must be zero.

What if there is a net electric charge within such a closed surface? Let us work through the following example.

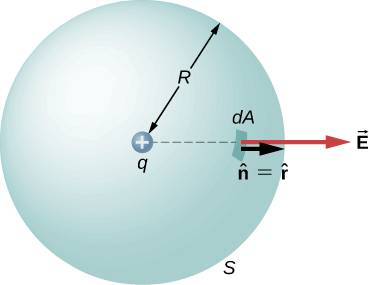
$$ \Phi = \oint_S \vec{E} \cdot \hat{n} dA = \oint_S E dA = \oint_S \frac{1}{4\pi\epsilon_0} \frac{q}{R^2} dA = \frac{q}{\epsilon_0} $$

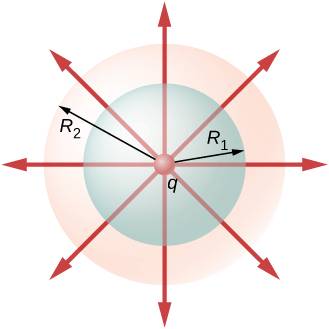
because $\oint dA = 4\pi R^2$. Amazingly, the flux is independent of the radius of the sphere. This fact can be verified using a visualization of electric field lines as well. The number of lines passing through the spherical surfaces of radii $R_1$ and $R_2$ are equal in the above figure (right).

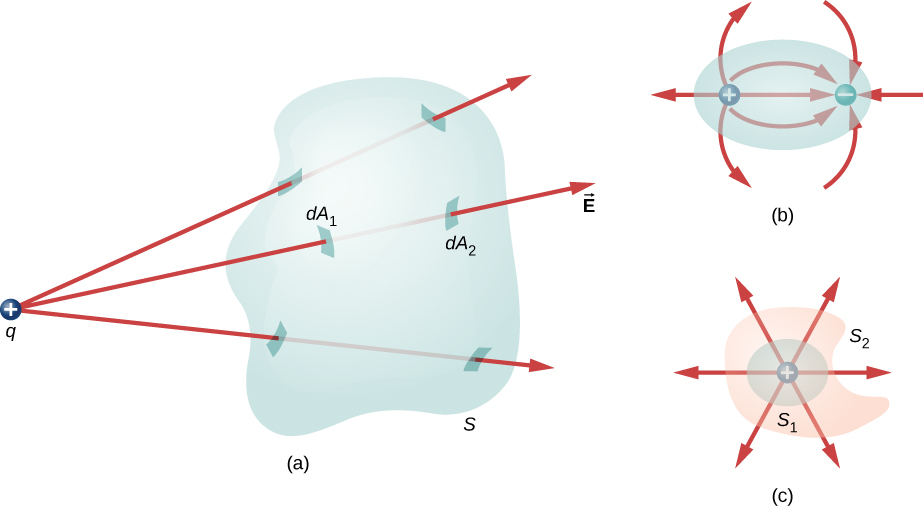
(a) If there is no net charge within the surface, number of lines going out and coming in are equal, and the net flux through the surface is zero. (b) There is a dipole inside the surface, net charge is zero, so net flux through the surface is zero as well. © The shape and size of the surface do not matter as long as the charge contained does not change.

This directly leads to the statement of Gauss’s law: the flux through a closed surface

\begin{equation} \Phi_c = \frac{q_e}{\epsilon_0} = \oint_S \vec{E} \cdot \hat{n} dA \end{equation}

where $q_e$ is the net charge enclosed within that closed surface and $\vec{E}$ is the net electric field on the surface caused by charges both outside and inside. It works for both positive and negative charges. For negative charges, flux is negative because the field lines are opposite to the outward normal vector.

When this law is used to claculate flux or field, the imagined surface is called a Gaussian surface.

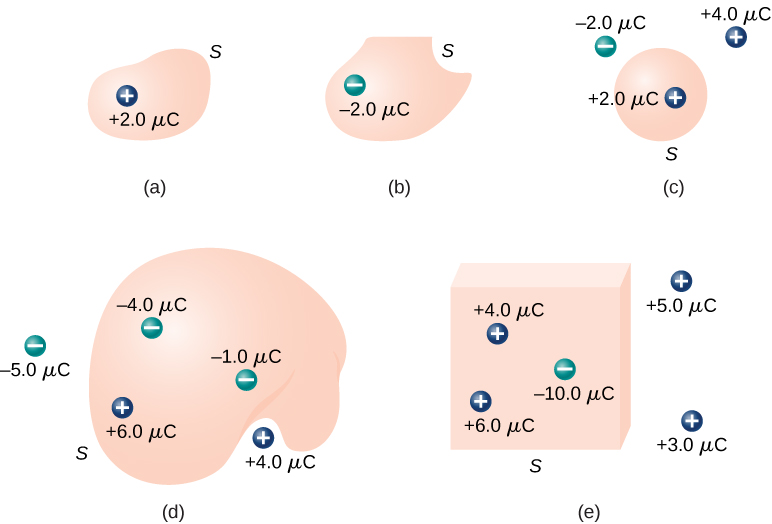
Calculate the electric flux through the above Gaussian surfaces. For example, (d) $\Phi = (-4+6-1)\times 10^{-6} C / \epsilon_0$. Here vacuum permittivity $\epsilon_0=8.85\times 10^{-12}$ C$^2$ m$^{-2}$ N$^{-1}$ and, hence, $\Phi\sim 10^5$ N m$^2$ C$^{-1}$.

For a spherically symmetric charge distribution

$$ \Phi = E \oint_S dA = 4\pi r^2 E = \frac{q_e}{\epsilon_0} $$

where $r$ is the distance of the Gaussian surface from the center of the sphere and $q_e$ is the net charge enclosed within the radius $R$ of the sphere. if we know $E$, we can calculate the enclosed charge.

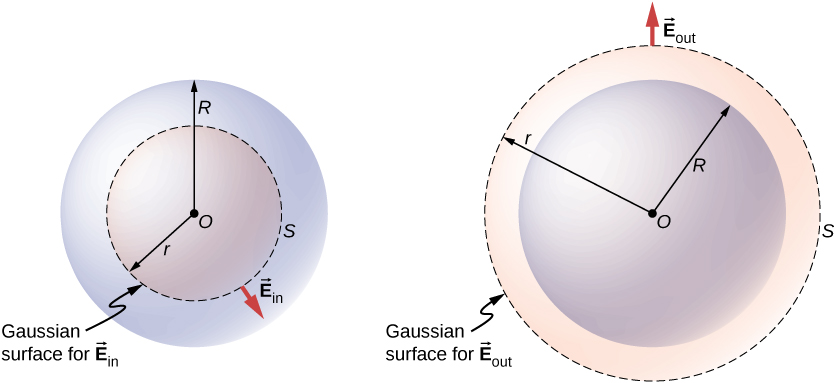
The imagined Gaussian surface can be inside ($r<R$, left panel) or outside ($r>R$, right panel) the sphere. In the first case the total charge within the sphere $q_t>q_e$ and in the second case $q_t=q_e$.

The calculation becomes easy if the sphere is uniformly charged with a volume charge density $\rho$ then

$$ q_e = \int \rho dV = \int_0^r \rho 4\pi r'^2 dr' = \frac{4}{3} \pi r^3 \rho $$

and hence the electric field for the outer Gaussian surface

$$ E_{out} = \frac{q_t}{4\pi\epsilon_0 r^2} = \frac{1}{4\pi\epsilon_0 r^2} \frac{4}{3} \pi R^3 \rho = \frac{\rho R^3}{3\epsilon_0 r^2} $$

and for the inner Gaussian surface electric field

$$ E_{in} = \frac{q_e}{4\pi\epsilon_0 r^2} = \frac{1}{4\pi\epsilon_0 r^2} \frac{4}{3} \pi r^3 \rho = \frac{\rho r}{3\epsilon_0}. $$

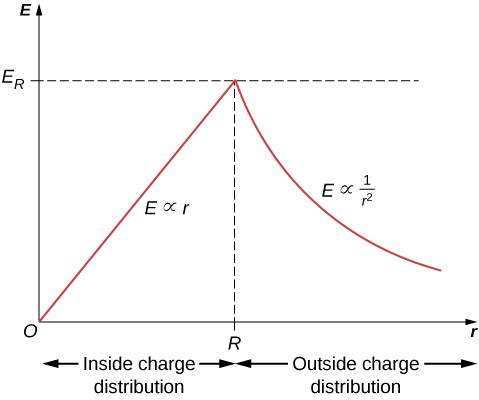
Remarkably, the field is proportional to distance inside the sphere and inversely proportional to the square of the distance outside the sphere.

A charged rod has cylindrical symmetry and Gauss’s law can be applied to simplify the problem of finding electric field or enclosed charge.

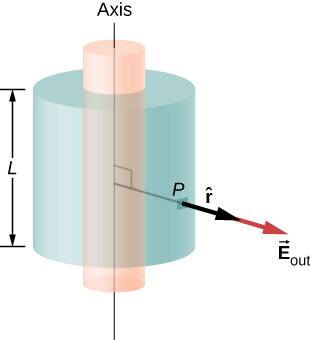
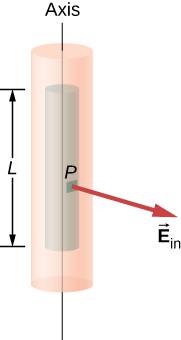
The chosen Gaussian surface is also cylindrical and has the same axis as the cylinder. The field is perpendicular to the area vector along the end caps and parallel along the cylindrical surface.

In this case, $\oint_S dA = 2\pi r L$ where $L$ is the length of the cylinder and $r$ the radius. Therefore electric flux

$$ \Phi = 2\pi r LE = \frac{q_e}{\epsilon_0} = \frac{\lambda L}{\epsilon_0} = 2\pi r LE $$

where $\lambda$ is the linear charge density in C/m. So the electric field

$$ E(r) = \frac{\lambda}{2\pi\epsilon_0} \frac{1}{r}. $$

Imagine a cylinder with all the charges only on its surface with a surface charge density $\sigma$. The linear density $\lambda = 2\pi R \sigma$ and, hence, the field for a Gaussian surface outside the cylinder

$$ E_{out} = \frac{2\pi R \sigma}{2\pi\epsilon_0 r} = \frac{\sigma R}{\epsilon_0} \frac{1}{r} $$

and inside the cylinder, $E_{in}= 0 / (2\pi\epsilon_0 r) = 0$ because there is no charge inside.

For a planar symmetry, the Gaussian surface should be a cube or box.

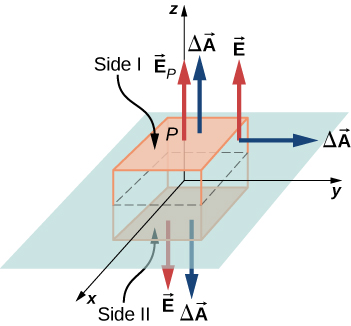
A cubic Gaussian surface around for a thin charged sheet. The flux along the 4 vertical surfaces is zero because the angle between the area vector and electric field is $90^\circ$. The net flux through the box is then

$$ \Phi = \oint_S \vec{E} \cdot \hat{n} dA = 2EA = \frac{q_e}{\epsilon_0} $$

and because $q_e=\sigma A$, the electric field

$$ \vec{E} = \frac{\sigma}{2\epsilon_0} \hat{n}. $$

So far we saw static charges inside an insulator. Inside a conductor, however, charges can move. Electric field inside a conductor is zero. If there is a field, electrons move and redistribute themselves in such a way that the net field becomes zero and electrostatic condition is re-established.

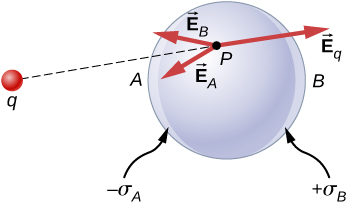
In this example the electric field at a point P outside the conductor $\vec{E}_P = \vec{E}_q + \vec{E}_A + \vec{E}_B = \vec{0}$ and also, according to Gauss’s law the net electric field at any point inside the conductor $\vec{E}=\vec{0}$.

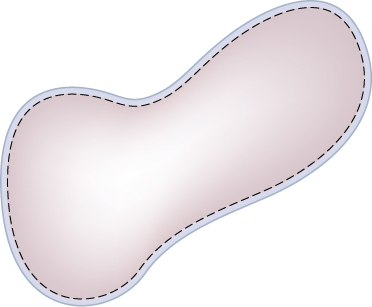
All the charges are concentrated on the surface. If a Gaussian surface (dashed line) is imagined exactly in the shape of the conductor and situated inside the conductor infinitesimally close the surface, then there is no charge inside the Gaussian surface.

Let us calculate the electric field on the surface of a conductor using Gauss’a law.

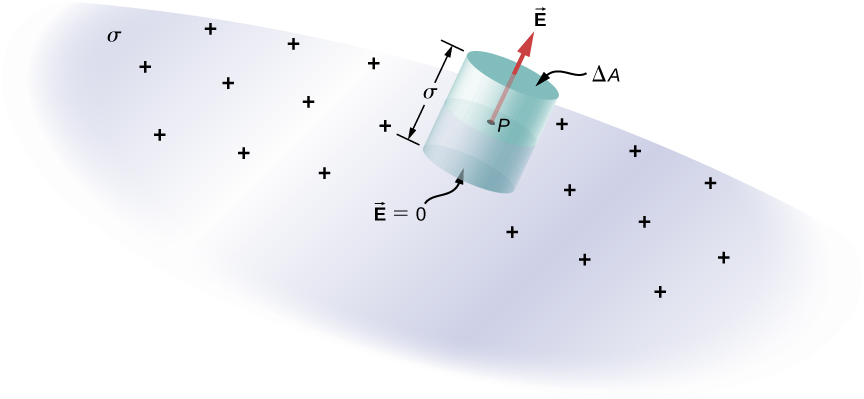
A Gaussian cylinder is imagined whose one end is inside the conductor and the other end outside. Flux is zero through the inner end and through the cylindrical surface. Only the outer end as nonzero flux. Hence,

$$ E\Delta A = \frac{\sigma\Delta A}{\epsilon_0} \Rightarrow E = \frac{\sigma}{\epsilon_0}. $$