Table of Contents
I. Electric charge and field
1. Electric charge
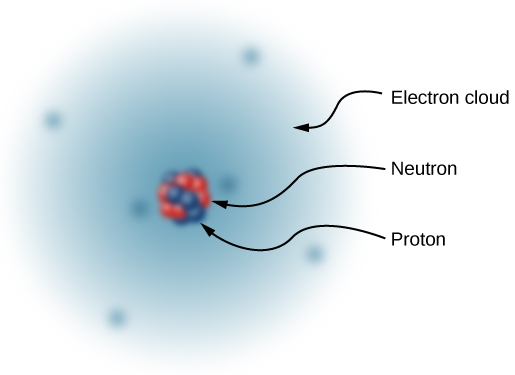
Atoms are the ultimate source electric charge. Atoms have positive protons and neutrals neutrons in their nucleus and negative electrons in a huge cloud surrounding the nucleus.
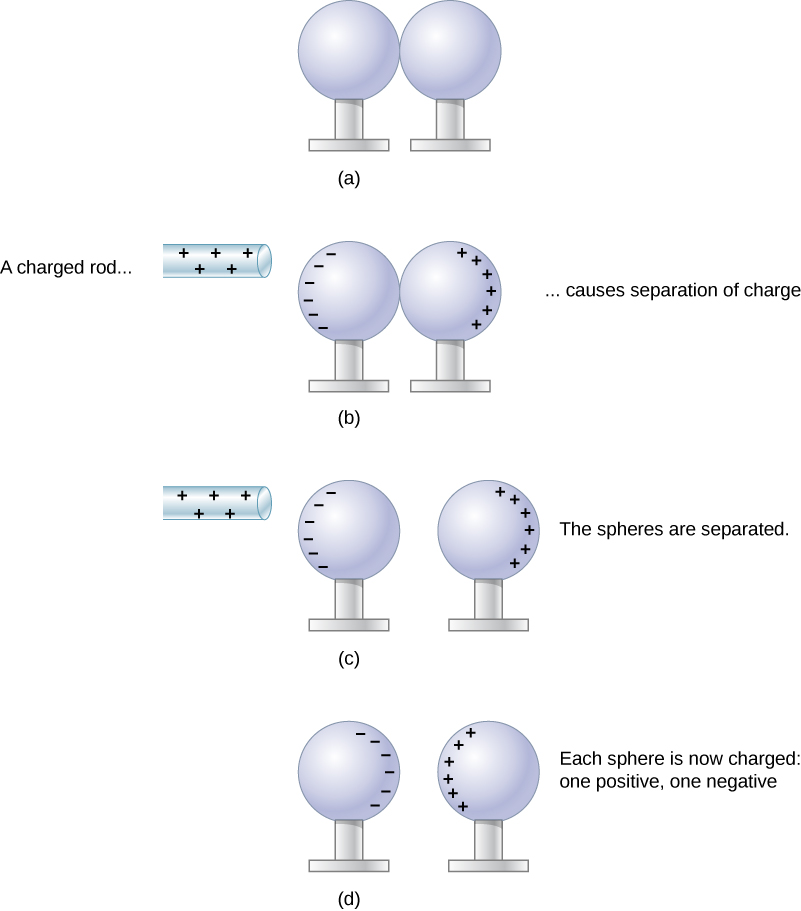
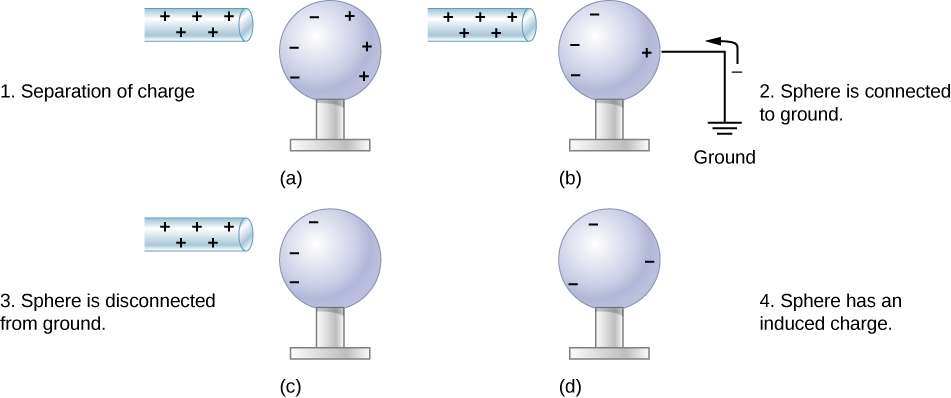
1.1 Charging

2. Coulomb's law
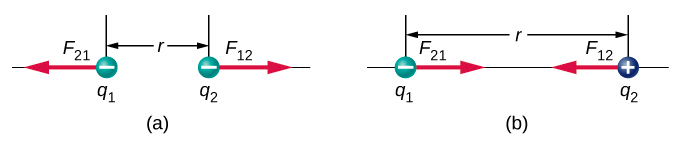

Superposition principle: $\overrightarrow{F}= \sum_n \overrightarrow{F_1}+\overrightarrow{F_2}+...+\overrightarrow{F_n}$
3. Electric field
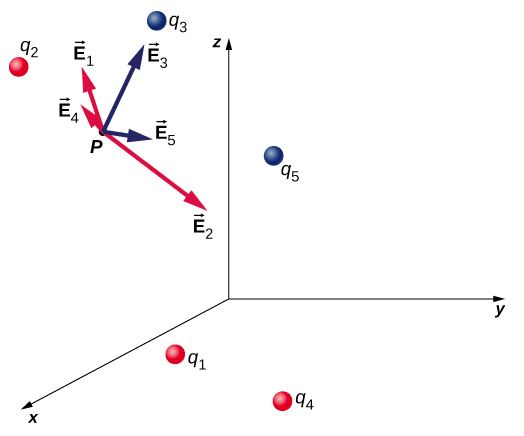
Compare with gravity
Vector field (E, g) and scalar field (T).
4. Electric field from charge
From point charges, let us turn to distribution of charges. In this case charge is measured using charge density. Charge density can be linear ($\lambda$), surface ($\sigma$) or volume ($\rho$).
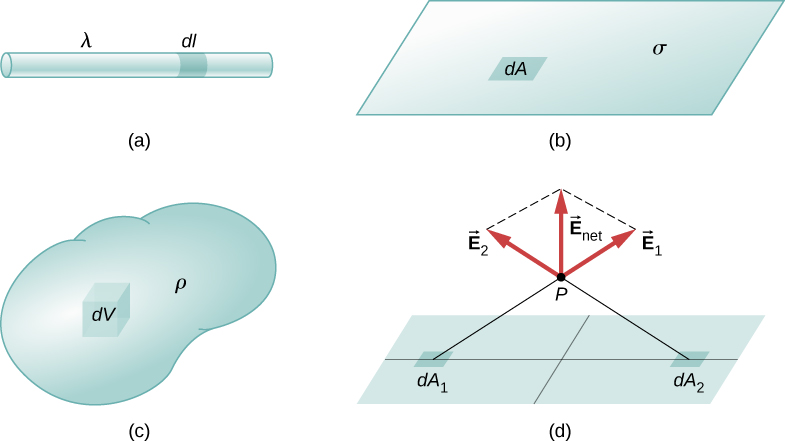
A differential charge element $dq = \lambda dl$ in one dimension, $\sigma dA$ in 2 dimensions and $\rho dV$ in 3 dimensions.
The net electric field at a point $P$ for different charges
\begin{align} \vec{E}(P) &= \underbrace{\dfrac{1}{4\pi \epsilon_0} \sum_{i=1}^N \left(\dfrac{q_i}{r^2}\right)\hat{r}}_{\text{Point charges}} \label{eq1}. \end{align}
If we have a continuous distribution of charges instead of discrete points, the summation becomes an integration over a line, surface or volume as shown below.
\begin{align} \vec{E}(P) &= \underbrace{\dfrac{1}{4\pi \epsilon_0} \int_{line} \left(\dfrac{\lambda \, dl}{r^2}\right) \hat{r}}_{\text{Line charge}} \label{eq2} \\[4pt] \vec{E}(P) &= \underbrace{\dfrac{1}{4\pi \epsilon_0} \int_{surface} \left(\dfrac{\sigma \,dA}{r^2}\right) \hat{r} }_{\text{Surface charge}}\label{eq3} \\[4pt] \vec{E}(P) &= \underbrace{\dfrac{1}{4\pi \epsilon_0} \int_{volume} \left(\dfrac{\rho \,dV}{r^2}\right) \hat{r}}_{\text{Volume charge}} \label{eq4} \end{align}
The vector integration indicates that there are in reality three different integrations for the three components $E_x(P)$, $E_y(P)$ and $E_z(P)$.
4.1 Line
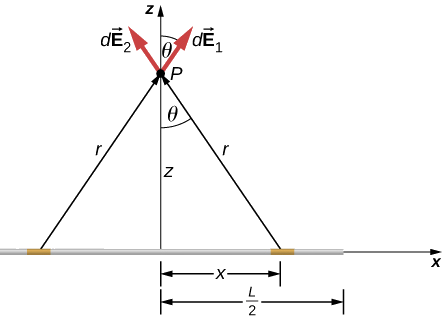
\begin{align*} \vec{E}(P) &= \vec{E}_1 + \vec{E}_2 \\[4pt] &= E_{1x}\hat{i} + E_{1z}\hat{k} + E_{2x} (-\hat{i}) + E_{2z}\hat{k}. \end{align*}
\begin{align*} \vec{E}(P) &= E_{1z}\hat{k} + E_{2z}\hat{k} \\[4pt] &= E_1 \, \cos \, \theta \hat{k} + E_2 \, \cos \, \theta \hat{k}. \end{align*}
\begin{align*} \vec{E}(P) &= \dfrac{1}{4 \pi \epsilon_0}\int \dfrac{\lambda dl}{r^2} \, \cos \, \theta \hat{k} + \dfrac{1}{4 \pi \epsilon_0}\int \dfrac{\lambda dl}{r^2} \, \cos \, \theta \hat{k} \\[4pt] &= \dfrac{1}{4 \pi \epsilon_0}\int_0^{L/2} \dfrac{2\lambda dx}{r^2} \, \cos \, \theta \hat{k} \end{align*}
Replace $r = (z^2 + x^2)^{1/2}$ and
$$\cos \, \theta = \dfrac{z}{r} = \dfrac{z}{(z^2 + x^2)^{1/2}}.$$
\begin{align*} \vec{E}(P) &= \dfrac{1}{4 \pi \epsilon_0}\int_0^{L/2} \dfrac{2\lambda dx}{(z^2 + x^2)} \dfrac{z}{(z^2 + x^2)^{1/2}} \hat{k} \\[4pt] &= \dfrac{1}{4 \pi \epsilon_0}\int_0^{L/2} \dfrac{2\lambda z}{(z^2 + x^2)^{3/2}} dx \hat{k} \\[4pt] &= \dfrac{2 \lambda z}{4 \pi \epsilon_0} \left[\dfrac{x}{z^2\sqrt{z^2 + x^2}}\right]_0^{L/2} \hat{k}. \end{align*}
which finally leads to
$$ \vec{E}(z) = \dfrac{1}{4 \pi \epsilon_0} \dfrac{\lambda L}{z\sqrt{z^2 + \dfrac{L^2}{4}}} \, \hat{k}. \label{5.12} $$
What happens when $z \gg L$: point charge.
If the line extends to infinity,
$$ \vec{E}(z) = \dfrac{1}{4 \pi \epsilon_0} \dfrac{2\lambda}{z}\hat{k}. \nonumber$$
4.2 Ring
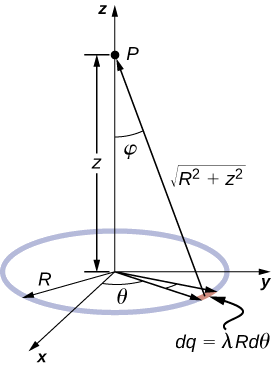
\begin{align*} \vec{E}(P) &= \dfrac{1}{4\pi \epsilon_0} \int_{line} \dfrac{\lambda dl}{r^2} \hat{r} = \dfrac{1}{4\pi \epsilon_0} \int_0^{2\pi} \dfrac{\lambda Rd\theta}{z^2 + R^2} \dfrac{z}{\sqrt{z^2 + R^2}} \hat{k} \\[4pt] &= \dfrac{1}{4\pi \epsilon_0} \dfrac{\lambda Rz}{(z^2 + R^2)^{3/2}} \hat{k} \int_0^{2\pi} d\theta \\[4pt] &= \dfrac{1}{4\pi \epsilon_0} \dfrac{2\pi \lambda Rz}{(z^2 + R^2)^{3/2}} \hat{k} \\[4pt] &= \dfrac{1}{4\pi \epsilon_0} \dfrac{q_{tot}z}{(z^2 + R^2)^{3/2}} \hat{k}. \end{align*}
What happens when $z \gg R$?
$$ \vec{E} = \frac{1}{4\pi\epsilon_0} \frac{q_{tot}}{z^2} \hat{k} $$
4.3 Disk
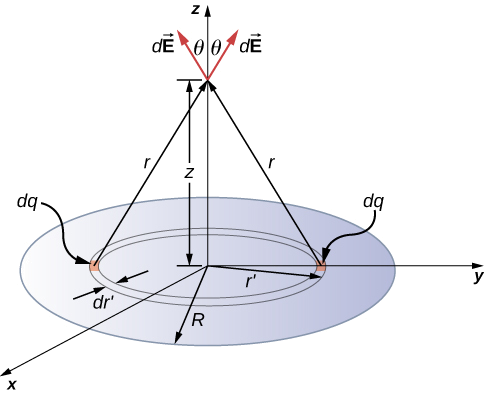
$$ \vec{E}(P) = \dfrac{1}{4\pi \epsilon_0} \int_{surface} \dfrac{\sigma dA}{r^2} \, \cos \, \theta \, \hat{k}. \nonumber $$
Here $dA = 2\pi r'dr'$ and $r^2 = r'^2 + z^2$ and
$$ \cos \, \theta = \dfrac{z}{(r'^2 + z^2)^{1/2}}. $$
Substituting all these in the first equation,
\begin{align*} \vec{E}(P) &= \vec{E}(z) \\[4pt] &= \dfrac{1}{4 \pi \epsilon_0} \int_0^R \dfrac{\sigma (2\pi r' dr')z}{(r'^2 + z^2)^{3/2}} \hat{k} \\[4pt] &= \dfrac{1}{4 \pi \epsilon_0} (2\pi \sigma z)\left(\dfrac{1}{z} - \dfrac{1}{\sqrt{R^2 + z^2}}\right) \hat{k} \end{align*}
If $R\rightarrow \infty$ you get an infinite plane and,
\begin{align} \vec{E} &= \lim_{R \rightarrow \infty} \dfrac{1}{4 \pi \epsilon_0} \left( 2 \pi \sigma - \dfrac{2 \pi \sigma z}{\sqrt{R^2 + z^2}}\right)\hat{k} \\[4pt] &= \dfrac{\sigma}{2 \epsilon_0} \hat{k}. \label{5.15} \end{align}
4.4 Planes
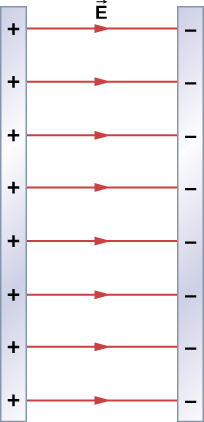
Electric field points away from positive charges and into the negative charges. Outside, the two planes the two fields cancel each other and inside they add up to give
$$ \vec{E} = \dfrac{\sigma}{\epsilon_0}\hat{i}. \nonumber $$
5. Field lines
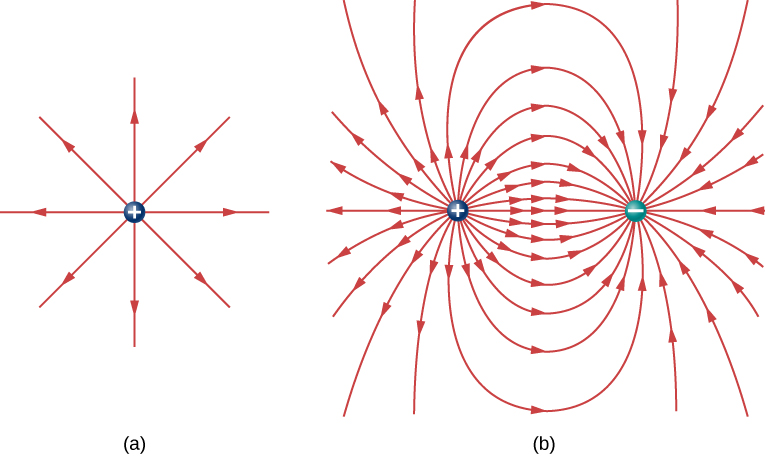

- Electric field lines either originate on positive charges or come in from infinity, and either terminate on negative charges or extend out to infinity.
- The number of field lines originating or terminating at a charge is proportional to the magnitude of that charge. A charge of 2q will have twice as many lines as a charge of q.
- At every point in space, the field vector at that point is tangent to the field line at that same point.
- The field line density at any point in space is proportional to (and therefore is representative of) the magnitude of the field at that point in space.
- Field lines can never cross. Since a field line represents the direction of the field at a given point, if two field lines crossed at some point, that would imply that the electric field was pointing in two different directions at a single point. This in turn would suggest that the (net) force on a test charge placed at that point would point in two different directions. Since this is obviously impossible, it follows that field lines must never cross.
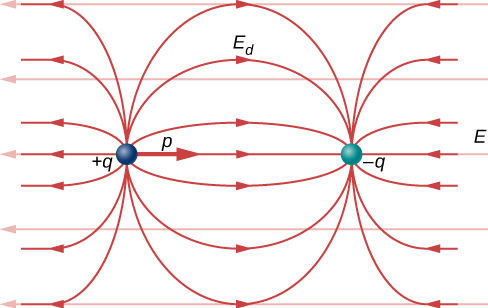
6. Electric dipole
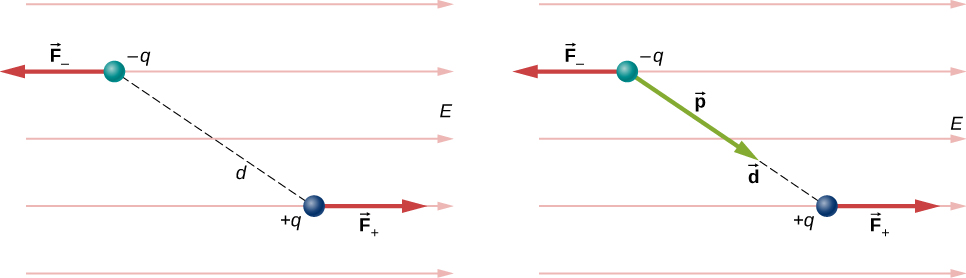
If $\vec{d}$ is the distance vector from the negative to the positive charge, the torque
\begin{align} \vec{\tau} &= \left(\dfrac{\vec{d}}{2} \times \vec{F}_+ \right) + \left(- \dfrac{\vec{d}}{2} \times \vec{F}_- \right) \\[4pt] &= \left[ \left(\dfrac{\vec{d}}{2}\right) \times \left(+q\vec{E}\right) + \left(-\dfrac{\vec{d}}{2}\right) \times \left(-q\vec{E}\right)\right] \\[4pt] &= q\vec{d} \times \vec{E}. \end{align}
where $\vec{p}=q\vec{d}$ is the dipole moment. Hence,
$$\vec{\tau} = \vec{p} \times \vec{E}.$$
Let us calculate the electric field of a dipole.
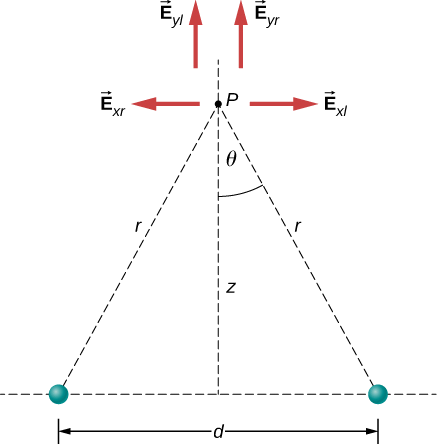
The vertical components of the field at point P cancels out. The horizontal component
\begin{align*} E_x &= \dfrac{1}{4\pi \epsilon_0} \dfrac{q}{r^2} \, \sin \, \theta + \dfrac{1}{4\pi \epsilon_0} \dfrac{q}{r^2} \, \sin \, \theta \\[4pt] &= \dfrac{1}{4\pi \epsilon_0} \dfrac{2q}{r^2} \, \sin \, \theta. \end{align*}
$$ r^2 = z^2 + \left(\dfrac{d}{2}\right)^2 \nonumber$$
$$ \sin \, \theta = \dfrac{d/2}{R} = \dfrac{d/2}{\left[z^2 + \left(\dfrac{d}{2} \right)^2\right]^{1/2}}. \nonumber $$
So
$$ \vec{E}(z) = \dfrac{1}{4\pi \epsilon_0} \dfrac{qd}{\left[z^2 + \left(\dfrac{d}{2}\right)^2\right]^{3/2}} \hat{i}.\label{5.6} $$
If $d \ll z \ll \infty$ then
$$ \vec{E}(z) = \dfrac{1}{4\pi \epsilon_0} \dfrac{qd}{z^3}\hat{i}. \nonumber $$