Table of Contents
3. Moment of inertia of a flywheel
1. Introduction and theory
$$ mgh = \frac{1}{2} m r^2 \omega^2 + \frac{1}{2} I \omega^2 + n_1 W $$
$$ \frac{1}{2} I \omega^2 = n_2 W \Rightarrow W = \frac{I\omega^2}{2n_2} $$
$$ I = \frac{2mgh - mr^2\omega^2}{\omega^2\left(1+\frac{n_1}{n_2}\right)} $$
$$ \frac{\omega+0}{2} = \frac{2\pi n_2}{t} \Rightarrow \omega = \frac{4\pi n_2}{t} $$
$$ h = 2\pi r n_1 $$
2. Method and data
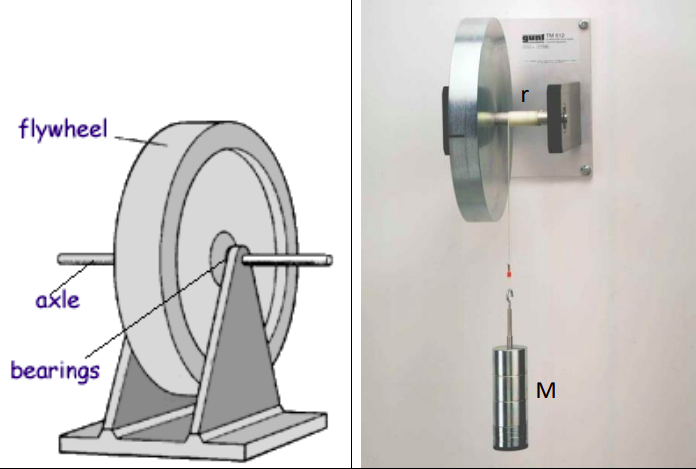
Number of rotations before the mass falls, $n_1=$
Radius of the axle, $r=[(a+vb)/2]$ cm; where $a$ is the main scale reading, $b$ is the Vernier scale reading, and $v$ is the Vernier constant.
| Mass [g] | $n_2$ | $t$ [s] |
|---|---|---|
| 1000 | ||
| 1500 | ||
| 2000 | ||
| 2500 |
3. Angular velocity
4. Moment of inertia
Mean
$$ \mu = \frac{1}{N} \sum_{i=0}^{N-1} x_i. $$
Standard deviation
$$ \sigma = \sqrt{ \frac{1}{N} \sum_{i=0}^{N-1} (x_i-\mu)^2}. $$
The final result of an experiment is quoted as
$$ \text{ value } = \mu \pm \sigma. $$
5. Discussion and conclusion
- Why does the flywheel come to a stop?
- Why are the 4 measurements of moment of inertia different?
- When does the flywheel reach its maximum velocity?
- What does the standard deviation (numpy.std) of $I$ tell you?