Table of Contents
1. Trajectory of a projectile
Report sample in Google Colab.
The report should have the following five sections. Each section must be written by a separate student. The whole report must be in a single Google Colab file and attached from Google Drive into the associated Google Classroom assignment.
1. Introduction and Theory
Any object projected in the gravitational field is called a projectile and its motion a projectile motion.

For such a motion, the magnitude of net acceleration $a=a_y=-g$, the gravitational acceleration, and the horizontal acceleration $a_x=0$. So horizontal velocity $v_x$ is always constant and the vertical velocity $v_y$ changes. The two perpendicular components are independent of each other. A set of 6 equations are needed for describing projectile motion. For the horizontal motion
$$ x = x_0 + v_x t $$
and for the vertical motion
$$ y = y_0 + \overline{v_y} t, $$ $$ y = y_0 + v_y t - \frac{1}{2} gt^2, $$ $$ v_y = v_{0y} - gt, $$ $$ v_y^2 = v_{0y}^2 - 2g(y-y_0) $$
where $\overline{v_y}$ is the average vertical velocity within a duration and $v_{0y}$ the initial vertical velocity.
The magnitude and direction of the velocity vector can always be found remembering the fact that $v_x=v\cos\theta$ and $v_y = v\sin\theta$ which means that the net velocity $v=\sqrt{v_x^2+v_y^2}$ and the angle of the velocity vector $\theta=\tan^{-1}(v_y/v_x)$.
From these equations of motion we can find three important quantities: maximum height, range and the trajectory. Maximum height of a projectile
$$ h = \frac{v_{0y}^2}{2g} = \frac{v_0^2\sin^2\theta}{2g}, $$
the range (maximum horizontal distance)
$$ R = \frac{v_0^2 \sin 2\theta_0}{g} $$
where $\theta_0$ is the initial angle, and the trajectory of the projectile is described as
$$ y = (\tan\theta)x - \frac{g}{2v_0^2\cos^2\theta} x^2 $$
which is the equation of a parabola in the form $y=Ax+Bx^2$. So the path taken by a projectile is always parabolic.
In this experiment, you will create such a parabolic path twice by releasing a marble ball from a ramp. The first part of the parabolic path will be from the end of the ramp to a point where the ball bounces, and the second part will be between the points of the first and second bounces.
You will measure different parameters of this trajectory, for example, the height of the ramp, the positions of the bounces and the maximum height of the second part of the trajectory. Using these parameters, you will calculate different velocity components and the energy, momentum and impulse related to this projectile. The aim is to get a complete description of a projectile including its impact with a horizontal surface.
2. Experimental Setup
For this experiment you have to use the following apparatus: a table, a bench, a ramp, some marble balls, 3 white recording papers, 3 carbon papers, some adhesive tape for fixing the papers on the table or bench, a long meter scale to measure long heights and lengths, a short meter scale for measuring short distances on the recording papers, and a weight scale to measure the mass of a ball.
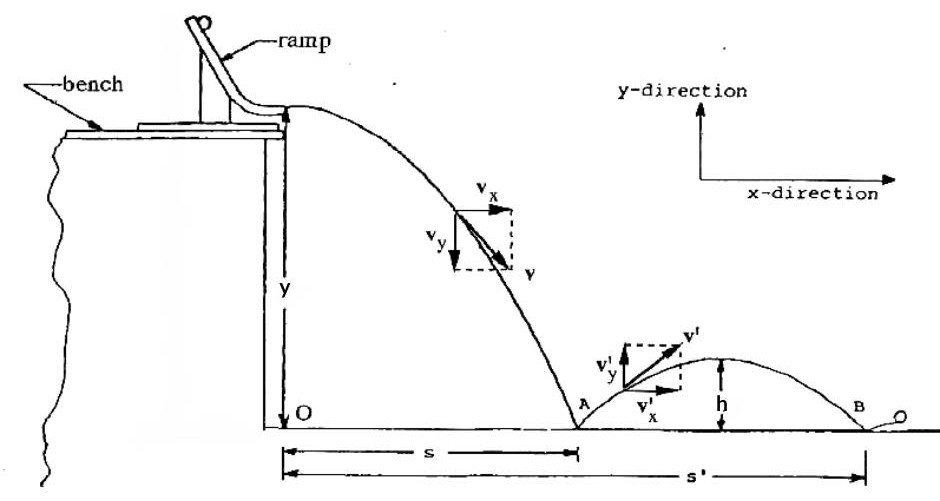
Describe how you set up the apparatus on the table.
3. Method and Data
| Quantity | Symbol | Value | Error ($\delta$) |
|---|---|---|---|
| Mass of the marble ball | $m$ | g | $\delta m=$ g |
| Height of the end of the ramp | $y$ | cm | $\delta y = $ cm |
| Position of the first bounce at A | $s$ | cm | $\delta s=$ cm |
| Position of the second bounce at B | $s'$ | cm | $\delta s'=$ cm |
| Maximum height between A and B | $h$ | cm | $\delta h = $ cm |
Describe how collected these data.
4. Analysis and Results
Using the five measurements you will have to calculate the following quantities.
4.1 Velocity
First, calculate the time for the ball to leave the ramp and reach point A which is $t = \sqrt{2y/g}$.
Horizontal component of the acceleration of the ball $a_x=0$, so the horizontal velocity of the ball $ v_x = s/t$. The vertical velocity of the ball just before it hits the table at point A would be $ v_y = -gt = -\sqrt{2gh}$.
From the maximum height $h$, you can calculate the time it took for the marble to go from points A to B ($t'$). We know $h=gt'^2/4$ and therefore $t' = \sqrt{4h/g}$. So the horizontal velocity of the ball after leaving A would be $ v_x' = (s'-s)/t'$. And the vertical component of the velocity of the ball after it leaves point A is $ v_y' = g t' / 2 $.
So the net velocity of the ball before it impacts at A is $v = \sqrt{v_x^2+v_y^2}$. And the net velocity of the ball after it impacts at A is $v' = \sqrt{v_x'^2+v_y'^2}$.
The angle of the trajectory before reaching A is $ \theta = \tan^{-1}(v_y/v_x) $ and after leaving A $ \theta' = \tan^{-1}(v_y'/v_x')$.
4.2 Kinetic energy
Kinetic energy of the ball before collision at point A
$$E = \frac{1}{2} mv^2.$$
Kinetic energy of the ball after collision at point A
$$E' = \frac{1}{2} mv'^2.$$
4.3 Momentum
Vertical component of the momentum before reaching A $P_y=mv_y$ and after leaving A $P'_y = mv'_y$.
Vertical component of the momentum before reaching A $P_x'=mv_x'$ and after leaving A $P'_x = mv'_x$.
So the net momentum before reaching A $p = mv$ and the net momentum after leaving A is $p' = mv'$.
4.4 Impulse
Vertical component of the impulse imparted on the ball by the table $J_y = p_y - p'_y$.
Horizontal component of the impulse imparted on the ball by the table $J_x = p_x - p'_x$.
5. Discussion and Conclusion
5.1 Discussion
Answer the following questions:
- What is the difference between systematic and stochastic error? Which errors in this experiment are systematic and which are stochastic?
- Why is $\delta s' > \delta h > \delta s$?
- Which velocity is greater, before reaching point A or after leaving A?
- Is the impulse positive or negative? Why?