Table of Contents
Questions and Problems
1. Second law
Before manned space flights, rocket sleds were used to test aircraft, missile equipment, and physiological effects on human subjects at high speeds. They consisted of a platform that was mounted on one or two rails and propelled by several rockets.
Calculate the magnitude of force exerted by each rocket, called its thrust T, for the four-rocket propulsion system shown below. The sled’s initial acceleration is 49 m/s$^2$, the mass of the system is $2100$ kg, and the force of friction opposing the motion is $650$ N.
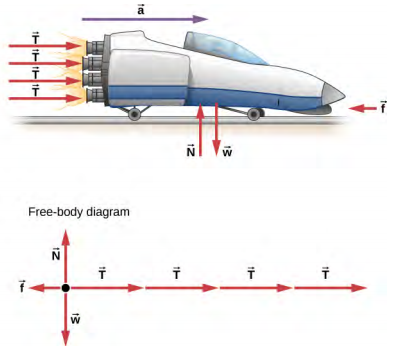
Use Example 5.4.
2. Force vectors
(A) Do the three quantities in Newton’s second law belong to the same particle or system? Explain.
(B) Several Forces on a Particle A particle of mass $m = 4.0$ kg is acted upon by four forces of magnitudes $F_1 = 10.0$ N, $F_2 = 40.0$ N, $F_3 = 5.0$ N, and $F_4 = 2.0$ N, with the directions as shown in the free-body diagram below. What is the acceleration of the particle?
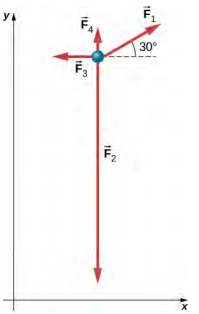
Use Example 5.7.
3. Mass and weight
(A) What is the difference between gravitational mass, inertial mass and weight?
(B) A farmer is lifting some moderately heavy rocks from a field to plant crops. He lifts a stone that weighs 180 N. What force does he apply if the stone accelerates at a rate of $1.5$ m/s$^2$?
Follow Section 6.
Use Example 5.5.1.
4. Combining the 3 laws
(A) A physics professor pushes a cart of demonstration equipment to a lecture hall as shown below. Her mass is $65.0$ kg, the cart’s mass is $12.0$ kg, and the equipment’s mass is $7.0$ kg. Calculate the acceleration produced when the professor exerts a backward force of $150$ N on the floor. All forces opposing the motion, such as friction on the cart’s wheels and air resistance, total $24.0$ N.
(B) Calculate the force the professor exerts on the cart in using data from (A) if needed.
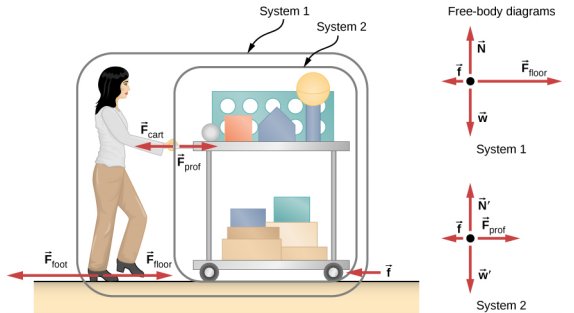
5. Different tensions
Consider the traffic light (mass of $15.0$ kg) suspended from two wires as shown below. Find the tension in each wire, neglecting the masses of the wires.
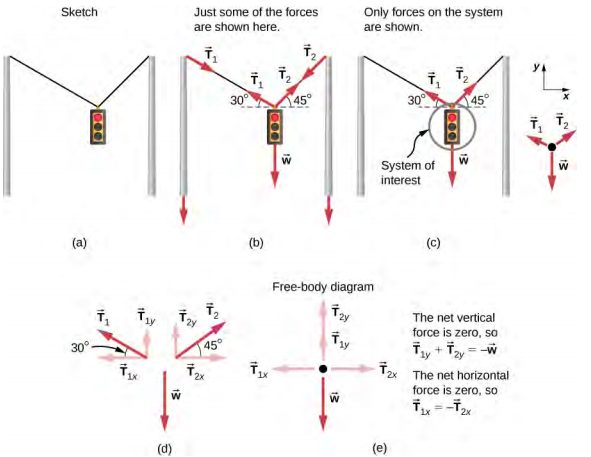
Follow Example 6.1.
6. Barge and boats
Two tugboats push on a barge at different angles (figure below). The first tugboat exerts a force of $2.7 \times 10^5$ N in the $x$-direction, and the second tugboat exerts a force of $3.6 \times 10^5$ N in the $y$-direction. The mass of the barge is $5.0 \times 10^6$ kg and its acceleration is observed to be $7.5 \times 10^{−2}$ m/s$^2$ in the direction shown. What is the drag force of the water on the barge resisting the motion?
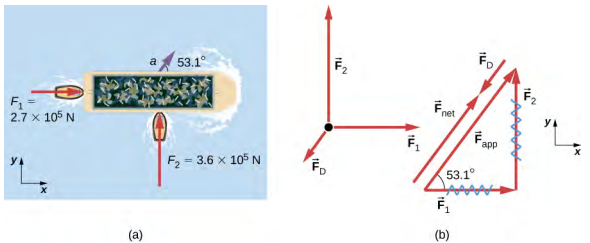
[Note: Drag force is a frictional force exerted by fluids, such as air or water. The drag force opposes the motion of the object. Since the barge is flat bottomed, we can assume that the drag force is in the direction opposite of motion of the barge.]
Use Example 6.2.
7. Weights on an elevator
The figure below shows a $75.0$-kg man standing on a bathroom scale in an elevator. Calculate the scale reading:
(A) If the elevator accelerates upward at a rate of $1.20$ m/s$^2$, and
(B) If the elevator moves upward at a constant speed of $1$ m/s.
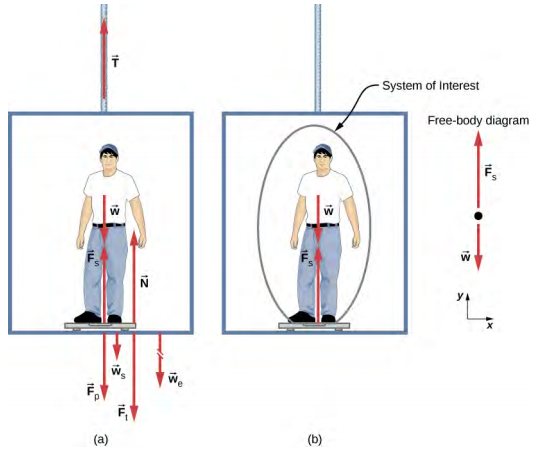
Follow Example 6.3.
8. Atwood machine
A classic problem in physics is that of the Atwood machine, which consists of a rope running over a pulley, with two objects of different mass attached. It is particularly useful in understanding the connection between force and motion. In the following figure, $m_1 = 2.00$ kg and $m_2 = 4.00$ kg. Consider the pulley to be frictionless.
(A) If $m_2$ is released, what will its acceleration be?
(B) What is the tension in the string?
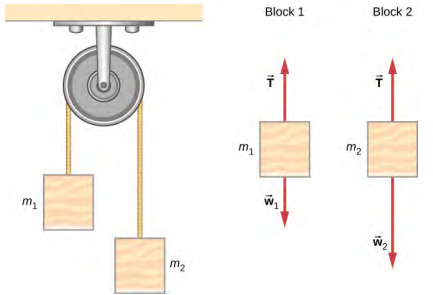
Follow Example 6.5.
9. Model helicopter
A $1.50$-kg model helicopter has a velocity $5.00 \hat{j}$ m/s at $t = 0$. It is accelerated at a constant rate for two seconds after which it has a velocity of ($6.00 \hat{i} + 12.00 \hat{j}$) m/s. What is the magnitude of the resultant force acting on the helicopter during this time interval?
Follow Example 6.7.
10. Static and kinetic friction
A $20.0$-kg crate is at rest on a floor as shown below. The coefficient of static friction between the crate and floor $\mu_s=0.700$ and the coefficient of kinetic friction $\mu_k=0.600$. A horizontal force $\overrightarrow{P}$ is applied to the crate. Find the force of friction if
(A) $P= 20.0$ N and $P = 30.0$ N, and if
(B) $P= 120.0$ N and $P = 180.0$ N.
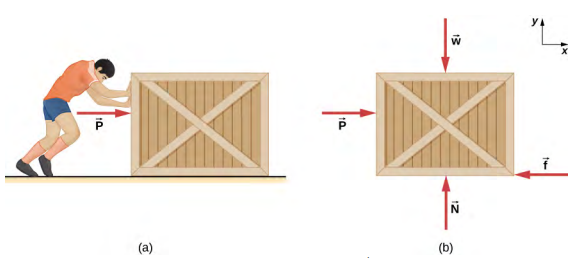
Follow Example 6.10.
11. Downhill skier
A skier with a mass of $62$ kg is sliding down a snowy slope at a constant velocity. Find the coefficient of kinetic friction for the skier if friction is known to be $45.0$ N.
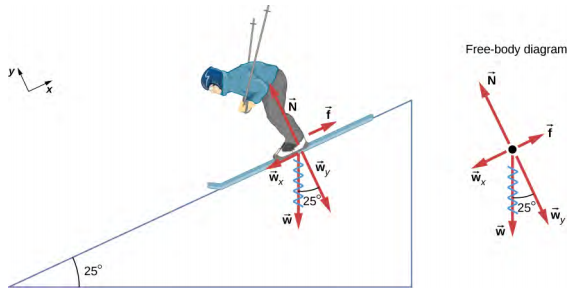
Follow Example 6.5.1.
12. Unbanked curve
(A) Calculate the centripetal force exerted on a $900.0$-kg car that negotiates a $500.0$-m radius curve at $25.00$ m/s.
(B) Assuming an unbanked curve, find the minimum static coefficient of friction between the tires and the road, static friction being the reason that keeps the car from slipping.
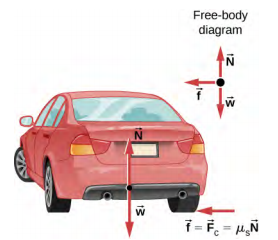
Follow Example 6.6.1.
13. Banked curve
Curves on some test tracks and race courses, such as Daytona International Speedway in Florida, USA, are very steeply banked. This banking, with the aid of tire friction and very stable car configurations, allows the curves to be taken at very high speed. To illustrate,
(A) derive an expression for calculating the banking angle necessary for making a curve at a certain speed, and
(B) calculate the speed at which a $100.0$-m radius curve banked at $31^\circ$ should be driven if the road were frictionless.
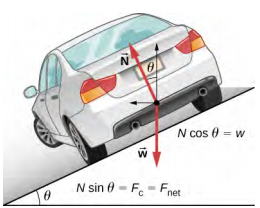
Follow Example 6.6.2.