Problems

On a six-string guitar, the high-E string has a linear density of $\mu_{hE} = 3.09 \times 10^{-4}$ kg/m and the low-E string has a linear density of $\mu_{lE} = 5.78 \times 10^{-3}$ kg/m.

a) If the high-E string is plucked, producing a wave in the string, what is the speed of the wave if the tension of the string is $56.40$ N?

b) The linear density of the low-E string is approximately 20 times greater than that of the high-E string. For waves to travel through the low-E string at the same wave speed as the high-E, would the tension need to be larger or smaller than the high-E string? What would be the approximate tension?

c) Calculate the tension of the low-E string needed for the same wave speed.

a) Tension force on the high-E string $F_T=56.40$ N. The wave speed on the high-E string

$$ v=\sqrt{\frac{F_T}{\mu_{hE}}} = 427.23 \text{ m/s}. $$

b) Wave speed is proportional to tension and inversely proportional to mass density. In order to keep the speed constant, if the density increases by a factor of 20 then the tension force on the string must also increase by a factor of 20. So the force would be around 1128 N.

c) The exact tension in the low-E string, $F_T=\mu v^2= 5.78\times 10^{-3} (427.23)^2 =1055$ N.

Consider a two-meter-long string with a mass of 70 g attached to a string vibrator (a spring that can create a wave on a string). The tension in the string is 90 N. When the string vibrator is turned on, it oscillates with a frequency of 60 Hz and produces a sinusoidal wave on the string with an amplitude of 4 cm and a constant wave speed. What is the time-averaged power supplied to the wave by the string vibrator?

Time-averaged power supplied by the wave $P=0.5 \mu\omega^2 A^2 v$.

Here, linear mass density $\mu=0.07/2=0.035$ kg/m.

Wave speed $v=\sqrt{F_T/\mu}=90/0.035=50.7$ m/s.

The angular frequency $\omega=2\pi f = 2\pi(60) = 377$ Hz.

So power $P=0.5 (0.035) (377)^2 (0.04)^2 50.7 = 201.5$ W.

Consider a string of L = 2.00 m attached to an adjustable-frequency string vibrator as shown in the figure.

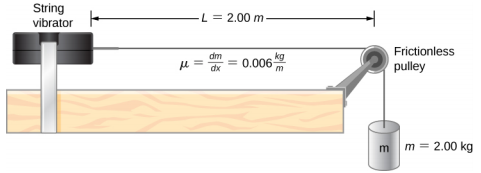
The waves produced by the vibrator travel down the string and are reflected by the fixed boundary condition at the pulley. The string, which has a linear mass density of μ = 0.006 kg/m, is passed over a frictionless pulley of a negligible mass, and the tension is provided by a 2.00-kg hanging mass.

a) What is the velocity of the waves on the string?

b) Draw a sketch of the first three normal modes of the standing waves that can be produced on the string and label each with the wavelength.

c) List the frequencies that the string vibrator must be tuned to in order to produce the first three normal modes of the standing waves.

a) The tension on the string is provided by the weight of the hanging mass. So wave speed $v=\sqrt{F_T/\mu}=\sqrt{mg/\mu}=\sqrt{2(9.8)/0.006}=57.15$ m/s.

b) The first normal mode has two nodes at either ends, so it must be a half wavelength long. The next two modes can be found my addition of half a wavelengths.

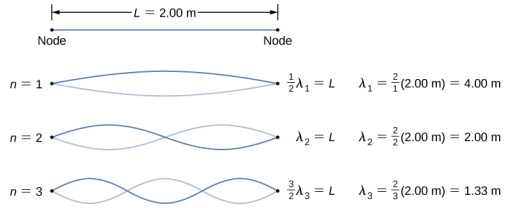
c) The first frequency $f_1=v/\lambda_1=57.15/4=14.29$ Hz.

Calculate the wavelengths of sounds at the extremes of the audible range, 20 and 20,000 Hz, in 30.0 °C air.

Speed of sound in air depends on temperature. $v=331\sqrt{T/273}$. At $30^\circ$ C, the speed

$$ v = 331\sqrt{\frac{303}{273}} = 348.7 \text{ m/s}. $$

The lowest and highest extremes of the audible range is 20 Hz and 20 kHz.

The wavelength of sound at the lowest extreme $\lambda_{max}=v/f_{min}=348.7/20 = 17$ m.

The wavelength at the highest extreme $\lambda_{min} = v/f_{max} = 348.7/20000 = 0.017$ m = 1.7 cm.

Calculate the sound intensity level in decibels for a sound wave traveling in air at 0° C and having a pressure amplitude of 0.656 Pa. Density of air at standard temperature and pressure is 1.29 kg/m$^3$.

Sound intensity is related to the amplitude of gauge pressure as $I=(\Delta P)^2/(2\rho v)$.

Here the pressure amplitude $\Delta P=0.656$ Pa. Speed of sound in air at $0^\circ$ C $v=331$ m/s. The density of air $\rho=1.29$ kg/m$^3$. So the intensity

$$ I = \frac{(\Delta P)^2}{2\rho v} = \frac{(0.656)^2}{2(1.29)331} = 5\times 10^{-4} \text{ W/m}^2.$$

The sound intensity level is measured with respect to $10^{-12}$ W/m$^2$. So the level

$$ \beta = 10 \log \frac{5\times 10^{-4}}{10^{-12}} = 10(\log 5 + \log 10^8) = 10(0.7+8) = 87 \text{ dB}. $$

Show that if one sound is twice as intense as another, it has a sound level about 3 dB higher.

Two speakers are separated by 5 m and are being driven by a signal generator at an unknown frequency. A student with a sound-level meter walks out 6.00 m and down 2.00 m, and finds the first minimum intensity, as shown below. What is the frequency supplied by the signal generator? Assume the speed of sound is $v = 343$ m/s.

The path length $r_1=\sqrt{6^2+2^2}=6.32$ m and $r_2=\sqrt{6^2+3^2}=6.71$ m.

So path length difference $\Delta r = |r_2-r_1| = 0.39$ m.

The first minimum occurs if the difference in path length is $\lambda/2$. So wavelength of the generated sound wave $\lambda = 2\Delta r = 0.78$ m.

So the frequency provided by the signal generator $f=v/\lambda=343/0.78=439.74$ Hz.

(a) What length should a tube closed at one end have on a day when the air temperature is 22.0 °C if its fundamental frequency is to be 128 Hz (C below middle C)?
(b) What is the frequency of its fourth overtone?