Table of Contents
1. Measurement and vectors
1. Fermi calculations
Physics deals with extremely small and large numbers simultaneously. For example, the table below shows some typical numbers for three different quantities: length (space), mass and time in units of m, kg and s, respectively.
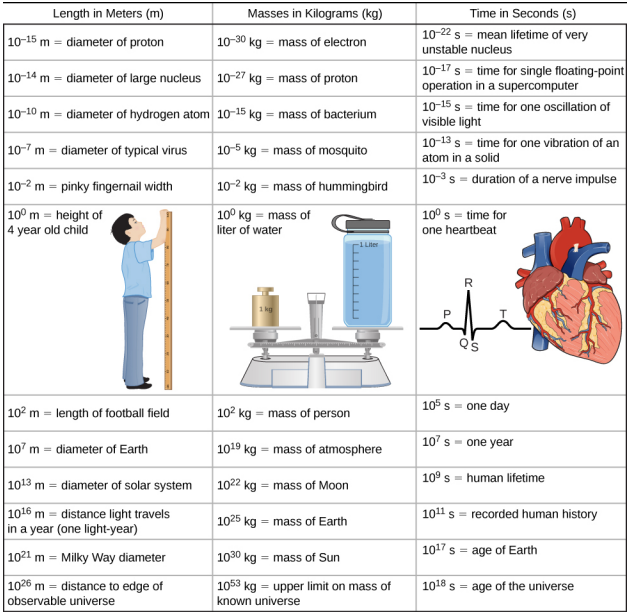
Do not memorize any of these numbers, but try to understand the scope and scale of the subject matter of physics by browsing through the table.
For example, how large is the distance to the edge of the observable universe compared to the diameter of a proton? The universe could be infinite (we do not know for sure), but the size of the radius of our observable universe, the portion of the universe we can observe via electromagnetic radiation $d_u = 10^{26}$ m. The diameter of a proton is around $d_p = 10^{-15}$ m. In order to compare these numbers, we have to calculate the ratio
$$ r_{up} = \frac{d_u}{d_p} = \frac{10^{26}}{10^{-15}} = 10^{26+15} = 10^{41}. $$
This is called an order of magnitude calculation or Fermi calculation (because Enrico Fermi popularized this type of calculation). We can say the radius of the observable universe is 41 orders of magnitude larger than the diameter of a proton or the universe is $10^{41}$ times larger than a proton.
Similarly the table tells us that the universe is $10^{53}/10^{-30} = 10^{83}$ times or 83 orders of magnitude heavier than an electron. On the other hand, the age of the universe is around $10^{18+22}$ or $10^{40}$ times or 40 orders of magnitude larger than the mean lifetime of a typical unstable nucleus.
You also see that $10^0$ m, $10^0$ kg and $10^0$ s are closely related to the world human beings experience. 1 m is the typical height of a 4-year-old child, 1 kg is the mass of 1 liter of water and 1 s is the average duration of a human heartbeat.
Read more from Section 1.2 and Section 1.6 of the textbook.
2. Units and prefixes
There are 7 base quantities from which all other quantities can be derived. All other quantities can be expressed as algebraic combinations of the base quantities and, hence, they are called derived quantities. The base quantities have base units and the derived quantities have derived units. All units can be expressed as algebraic combinations of base units.
International Organization for Standardization (ISO) recommends using the following seven base quantities which form the International System of Quantities (ISQ). They are used to define seven corresponding units that form the International System of Units (SI).

| ISQ Base Quantity | SI Base Unit |
|---|---|
| Length | meter (m) |
| Mass | kilogram (kg) |
| Time | second (s) |
| Electrical current | ampere (A) |
| Temperature | kelvin (K) |
| Amount of substance | mole (mol) |
| Luminous intensity | candela (cd) |
To give you an example of how other quantities can be derived from these seven, let us take Newton’s famous equation $F=ma$.
3. Unit conversion and consistency
4. Vectors
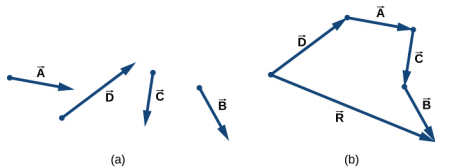
4.1 Geometric approach
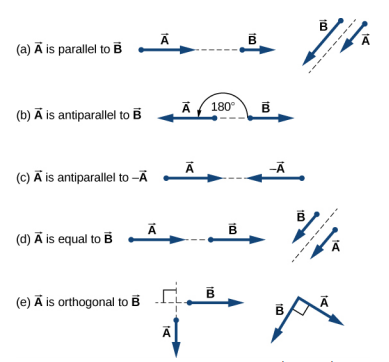
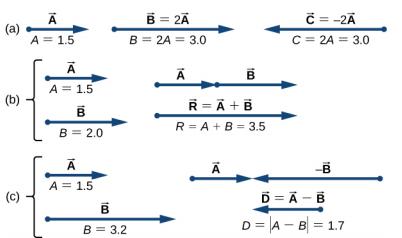
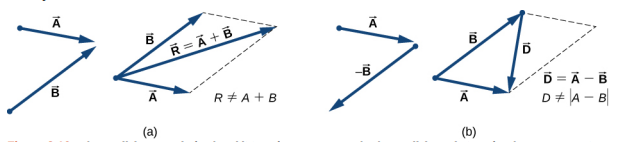
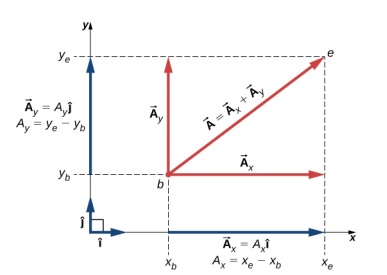
4.2 Algebraic approach
4.2.1 Components
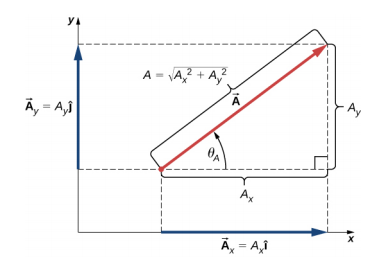
4.2.2 Addition and subtraction
4.2.3 Multiplication