Table of Contents
1. Road to reality
Astronomical numbers
We will deal with a lot of large or astronomical numbers. The best way to deal with these numbers is through orders of magnitude.
I can write that the age of the universe is either 14 billion (giga) years or $14\times 10^9$ years. Another way of saying $10^9$ is 10 orders of magnitude.
A number that only tells you how many zeros to put after $1$ is in the form of orders of magnitude. Nine orders of magnitude or $10^9$ means that there are 9 zeros after 1.
Calculations become very easy and calculators are never needed when we stick to only orders of magnitude. Let us calculate the mass of the universe in order to demonstrate this counterintuitive fact.
There are approximately 100 billion stars in a typical galaxy.
Units and prefixes
| Quantity | Unit | Symbol |
|---|---|---|
| Length | meter | m |
| Time | second | s |
| Mass | kilogram | kg |
| Prefix | Order of 10 | English word | |
|---|---|---|---|
| tera | T | $10^{12}$ | trillion |
| giga | G | $10^9$ | billion |
| mega | M | $10^6$ | million |
| kilo | k | $10^3$ | thousand |
| $10^0$ | one | ||
| milli | m | $10^{-3}$ | thousandth |
| micro | μ | $10^{-6}$ | millionth |
| nano | n | $10^{-9}$ | billionth |
| pico | p | $10^{-12}$ | trillionth |
Space and time
Time and river
Evolution
Poetry
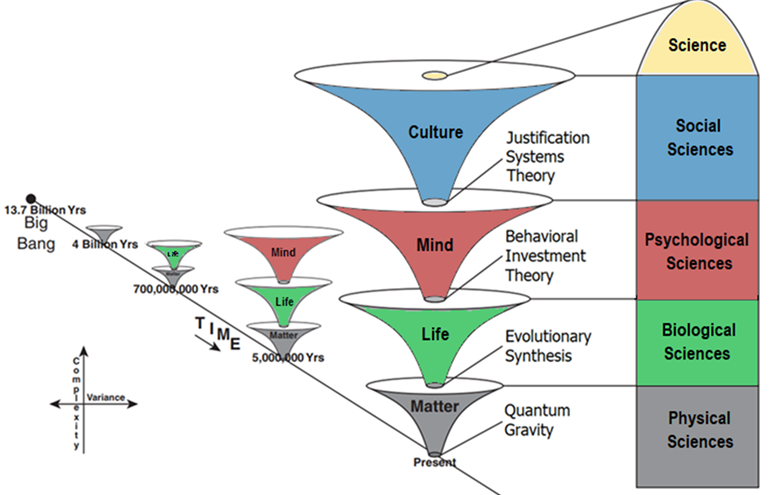
Cosmos and universe
There are two terms for ‘everything that exists’ in English, one from Greek, one from Latin. Cosmos is Greek in origin and it means order; it is related to the Sanskrit word samsati which has the same connotations. On the other hand, Universe is Latin in origin and has a complex set of meanings.
On first encounter, ‘universe’ seem to just mean ‘one poem’ (uni + verse).
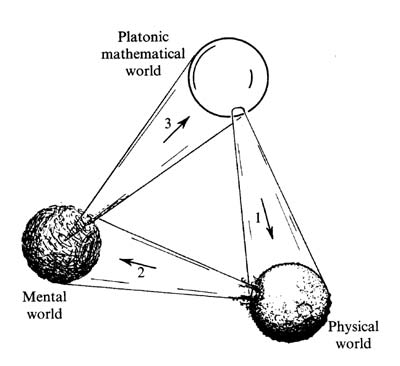
Three possible realms
Book: Road to Reality by Roger Penrose.
Tree of knowledge