7. Astronomical telescopes

“The adventure is not to see new things, but to see things with new eyes.” — Marcel Proust

For a ground-based telescope, the mount moves the telescope to point to a particular object and then track the object throughout a observation.

Transit or ‘drift-scan’ telescopes do not track but observe a particular region toward the zenith all the time. The spin of the Earth brings different parts of the sky within the FoV of such a telescope.

Ground-based telescopes have two main types of mounts: altazimuth and equatorial.

Altazimuth: rotate the the vertical axis to different azimuths, and horizontal axis to different altitudes.

Equatorial: rotate the polar axis (pointed toward the north celestial pole) to different hour angles, and the declination axis to different declinations. The hour angle is the sidereal time minus the right ascension (RA). So the mount directly tracks the RA and DEC.

Equatorial mount is simpler for pointing and tracking, but more expensive and clumsy in terms of construction. All ground-based telescopes above a diameter of 5 m use altazimuth mount.

Advantage of altazimuth mount is that the gravitational load does not vary with pointing direction in this case. But the main disadvantage is the complex tracking. Both the axes have to moved simultaneously with varying speed as a function of time.

Almost all modern telescopes are reflecting telescopes.

In prime focus telescopes, the astronomer or her remote-controlled detectors or instruments are located at the focal plane of the paraboloid primary mirror. As the detectors block parts of the light going to the primary mirror, this configuration works well only if the size of the detectors is small compared to the primary mirror. For mirrors larger than around 3.5 meters, the instruments are located in a prime focus cage.

For focused images, the central obstruction has minimal effect, but out-of-focus images have a ‘doughnut’ shape. The support structure of the prime focus cage, that connects it to the side of the optical tube, also creates ‘diffraction spikes’ on very bright stars.

The length of the coma effect for these telescopes, $L_c = \theta/16\mathcal{R}^2$ and for astigmatism $L_a=\theta^2/2\mathcal{R}$ where $\mathcal{R}$ is the focal ratio $f/D$ and $\theta$ is the angular distance of the image from from the optical axis.

An alternative to prime focus is Newtonian focus, where the light is reflected away from the focal plane to the side of the tube where the detectors and instruments are located. Light is redirected using a diagonal mirror at the focal plane. Professional astronomers do not really use Newtonian anymore, they prefer Cassegrain.

Neither the prime focus nor the Newtonian designs are good enough for modern professional astronomy because they require placing the astronomer or the instruments directly at the focal plane which is challenging, especially when the focal length is large. Also any weight at the focus creates a variable torque on the optical tube.

The Cassegrain and Gregorian designs are shown above. In Cassegrain design, a convex hyperboloid secondary mirror is placed in front of the paraboloid primary so that the virtual focus of the secondary mirror coincide with the focus of the primary mirror. Light is collected at the second focus of the hyperboloid at $F'$. The Gregorian uses the same method with the exception that the secondary is a concave ellipsoid.

The parameters of a two-mirror telescope are defined in reference to the above diagram. Final power

$$ P = \frac{1}{f} = P_1 + P_2 - dP_1P_2 $$

where $P_1$ and $P_2$ are the powers of the primary and secondary, respectively. Three dimensionless parameters describe the final focal length $f$, the distance between the primary and secondary $d$, and the back focal distance $z_F$. The respective dimensionless parameters are

$$ m = \frac{P_1}{P} = \frac{f}{f_1} = -\frac{s_2'}{s_2} $$

$$ k = \frac{y_2}{y_1} = 1-\frac{d}{f_1} $$

$$ \beta = \frac{z_F}{f_1} $$

where $\beta$ is positive if the focus is behind the primary, and $m$ and $k$ are positive for aCassegrain and negative for a Gregorian. Only two of these parameters might be enough as

$$ k = \frac{1+\beta}{1+m}. $$

The tube of the Cassegrain is much shorter than a Newtonian which means Cassegrain is much cheaper to build. A Gregorian is longer than a Cassegrain but still shorter than a Newtonian.

The conic constant for the primary $K_1=-1$ (paraboloid) for both, and for Cassegrain the conic constant for the secondary

$$ K_2 = -\left(\frac{m+1}{m-1}\right)^2 $$

which is determined by the requirement that SA should be zero.

Both Gregorian and Cassegrain have $K=-1$ which means they cannot avoid coma and astigmatism. But an aplanatic (without coma and astigmatism) two-mirror telescope called the Ritchey–Chrétien (RC) is made using a primary mirror of different. In an RC, both the primary and secondary are hyperboloid and their conic constants

$$ K_1 = K_{1c} - \frac{2(1+\beta)}{m^2(m-\beta)} $$

$$ K_2 = K_{2c} - \frac{2m(m+1)}{(m-\beta)(m-1)^3} $$

where $K_{1c}$ and $K_{2c}$ are the conis constants of the Cassegrain.

RC reduces coma and astigmatism, but the other aberrations are higher in RC than in Gregorian. But Gregorian has longer tube and greater central obstruction due to the concave paraboloid. So RC is the design of choice in many cases.

Below panel (a) shows the Nasmyth focus and (b) the coudé focus. Both are used in cases when heavier instruments need to be placed at the final focus. Nasmyth can take heavier instruments than Cassegrain and RC, but coudé can take even more load than Nasmyth.

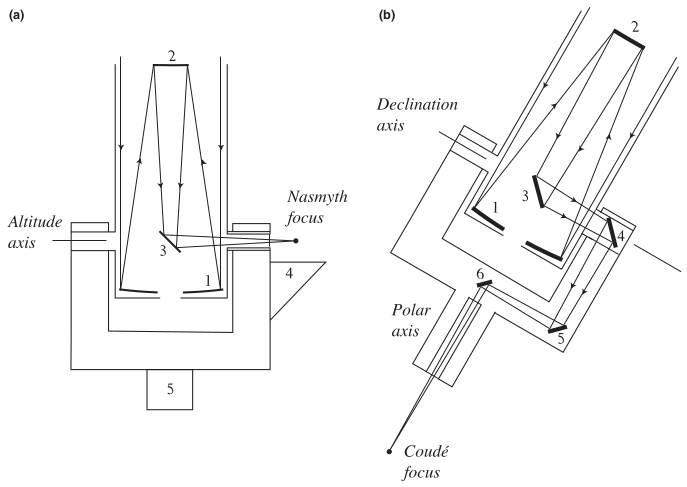
In (a) a flat mirror intercepts the light from the secondary and redirects it horizontally along the altitude axis to the Nasmyth focus which remains fixed relative to the mount during tracking. Gravitational stress on the telescope and mount do not change over time for this.

In (b) (shown in an equatorial mount here) the light from the secondary is intercepted and, first, brought along the declination axis and then to the polar axis.

RC can give good quality images for up to 1 deg, and maybe up to 3 deg with corrector lenses. Schmidt telescopes are used for larger field of view, 6 to 8 deg. They are specially good for photographic surveys.

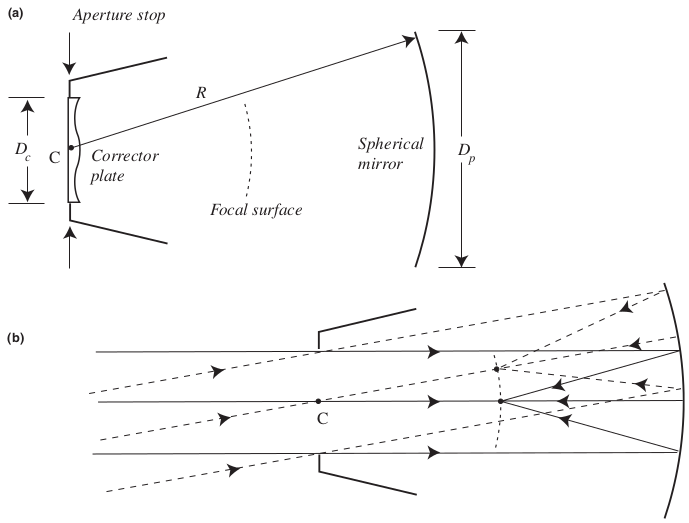
In this configuration, a spherical mirror is used as primary and an aperture stop is placed at the center of curvature of the primary to remove SA. A corrector plate is placed on top of the aperture stop.

Light from different angles illuminate different parts of the primary, and the focal surface, but the chief ray from any direction always passes through $C$. So $b=0$ and all off-axis aberrations are gone.

The corrector plate then removes SA. The marginal rays ($\rho$ large) converge more strongly than the axial rays ($\rho$ small, closer to axis) as you saw in Section 5.3 of Chapter 6. A Schmidt corrector has higher power for the axial rays than for the marginals, this bringing all rays to a common focal plane.

$$ \theta = 2\alpha = \frac{2.44 \lambda}{D} $$

The number of photons detected by a detector is the Signal

$$ S = \frac{\pi D^2}{4} \frac{\lambda}{hc} f_\lambda tQ $$

where the factor $hc/\lambda$ converts from the energy units to number of photons, $Q$ is a factor dependent on the bandwidth and efficiency of the detector, $t$ is the exposure (integration) time, and $f_\lambda$ is the actual flux from the object at a particular wavelength.

A star is detectable if $S$ is about the same size as its uncertainty. The measurement

$$ M = S+B $$

where $B$ is the background containing everything other than the star in the image. The background can actually be both in front of the star or behind star or at the same distance as the star. The background

$$ B = \frac{\pi D^2}{4} \frac{\lambda}{hc} \frac{\pi\theta^2}{4} b_\lambda tQ $$

where $\theta$ is the size of the star in the image and $b_\lambda$ the actual background flux. Now according to Poisson statistics the uncertainty in counting photons, the noise,

$$ N = \sigma(S) = \sqrt{(S+B)+B} \approx \sqrt{2B} = \frac{\pi D\theta}{4} \left(\frac{2\lambda b_\lambda tQ}{hc}\right)^{1/2} $$

and, thereby, the signal-to-noise-ratio (SNR)

$$ \frac{S}{N} \approx \left(\frac{\lambda Qt}{hcb_\lambda}\right) \frac{D}{\theta} f_\lambda $$

for a star that is marginally detectable. Purring $S/N=1$ results in the flux of such a star

$$ f_\lambda = \sqrt{\frac{hc}{\lambda Q}} \sqrt{\frac{b_\lambda}{t}} \frac{\theta}{D} $$

for a telescope whose image results in the diameter of a star to be $\theta$. In case of ground-based telescope, the size is that of the seeing disk. For space telescope putting $\theta=2.44\lambda / D$ gives

$$ f_{d,space} = \sqrt{\frac{hc\lambda}{Q}} \sqrt{\frac{b_\lambda}{t}} \frac{2.44}{D^2} $$

which means, increasing the aperture size gives a huge advantage in case of space telescopes because $f_d \propto D^{-2}$ in that case.

Advantages are as follows.

1. Background $b_\lambda$: the darkest background for HST is $23.3$ mag arcsec$^{-2}$, and the background for the darkest ground-based telescopes is $22.0$ mag arcsec$^{-2}$. For JWST, the sky at 5 $\mu$m is 12 mag darker in space than on the darkest ground.
2. Atmospheric transmission
3. Visible sky area
4. Gravitational and frictional stress

Disadvantages are as follows.

1. Cost. One 8-m Gemini telescope cost 100 million USD, and one 2.4-m HST telescope cost 2 billion USD.
2. Thermal stress
3. Harmful radiation, high-energy particles

The Hale telescope had 5-m mirror made of Pyrex glass and weighed 14 tons. The paraboloidal mirror needs a moving support structure that weighs 530 tons. Completed in 1949, it set the standard of the time. There are 3 stages of making a mirror.

1. Casting: molten glass poured into a cylindrical mold
2. Annealing
3. Grinding and polishing