Space, time and motion

In order locate an astronomical object, we need to define a coordinate systems. The most widely used system is the spherical coordinate system $(r,\theta,\phi)$ related to the Cartesian coordinate system $(x,y,z)$. We basically need 4 steps to define such a system:

1. Origin: the center of the Earth, Sun or our Galaxy.
2. Fundamental plane: the $x-y$ plane, plane of the Earth’s equator, the solar system or the Galaxy.
3. Fundamental direction: direction of the positive $x$-axis, e. g. the direction from the Sun to the Galactic center.
4. Sign convention: convention for the signs of $y-$ and $z$-axes.

The fourth step can give rise to either a left-handed (left panel above) or a right-handed (right panel) system. In the right-handed system, the right hand is used to determine the direction of positive $\phi$ and $\theta$ from the $x$- and $z$-axis, respectively. In the left-handed system, the left hand is used to determine the direction of positive $\lambda$ and $\xi$ from the $x$- and $z$-axis, respectively.

For a Cartesian system, the distance between any two points is given by Pythagoras’ theorem:

$$ d = \sqrt{x^2+y^2+z^2}. $$

If we are mainly interested in defining positions on a spherical surface, we seldom need the $r$ coordinate which is basically the distance of an object from the center of the Earth. Let us focus on the surface for now.

A great circle is the circle created by the intersection of the surface and a plane passing through the center. A small circle is created when the plane does not pass through the center. A distance on the surface is an arc of a great circle. The sides of a spherical triangle on the surface are arcs of three different great circles and such a triangle follows some rules. The law of cosines says

$$ \cos a = \cos b \cos c + \sin b \sin c \cos A $$

$$ \cos A = \cos B \cos C + \sin B \sin C \cos a $$

and the law of sines says

$$ \frac{\sin a}{\sin A} = \frac{\sin b}{\sin B} = \frac{\sin c}{\sin C} $$

where $A,B,C$ are the angles and $a,b,c$ are the sides opposite to the angles.

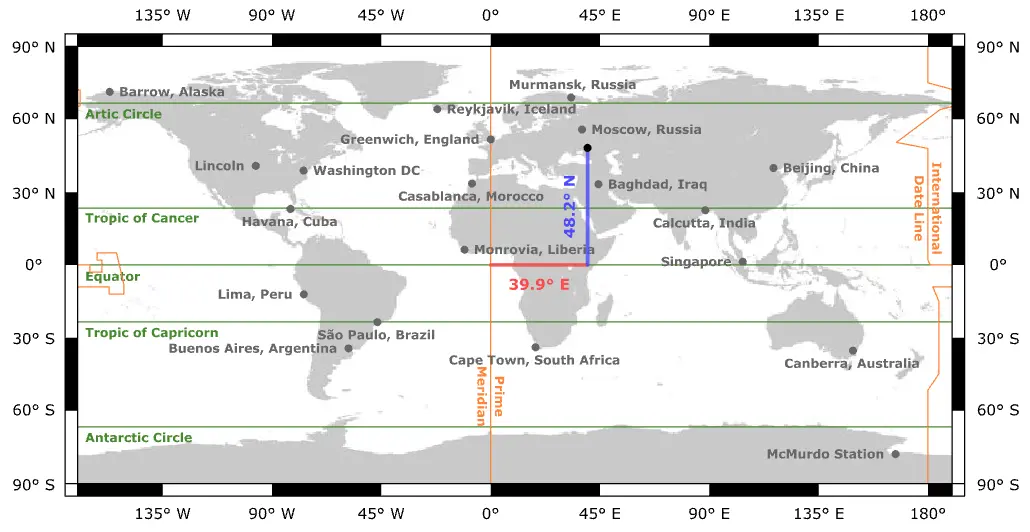
In the terrestrial coordinate system, i. e. the latitude-longitude system, we define the center of the Earth as the origin, the equatorial plane of the Earth as the fundamental plane, the direction from the center of the Earth to the prime meridian as the positive $x$-axis, and then we use the left hand to define the direction of positive longitude $\lambda$ from the prime meridian, and the direction of positive latitude $\beta$ from the equatorial plane. Great circles perpendicular to the equator are called meridians and they pass both the north and south poles. The meridian passing through the Greenwich Observatory (UK) $G$ is the prime meridian.

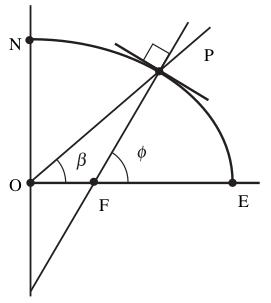
The geocentric latitude $\beta$ is different from the geodetic latitude $\phi$ as shown above. In the geodetic system, the latitude is defined a line that is perpendicular to the actual spheroid (ellipsoid of revolution) that the Earth actually is. Here the line $PF$ is perpendicular to the spheroidal surface of the Earth and points toward the gravitational force toward the center. GPS uses the geodetic system. There is one more latitude, the geographic latitude which is the angle between the local vertical and the equator which might not be the same as the geocentric or the geodetic latitude.

Planetary scientists or planetologists define latitude-longitude system for other planets as well using a distinguishing mark on its surface to establish the prime meridian. In any planet, the north pole is defined as the pole that is north of the ecliptic, the plane containing the Earth’s orbit.

A system defined with respect to the horizon of an observer on the surface of the Earth. The location of the observer is the origin $O$, the fundamental plane is the horizontal plane which is tangent to the spherical earth at point $O$ and intersects the celestial horizon at points NEWS. Vertical circles are perpendicular to the horizon and pass through the zenith ($T$) and nadir. The vertical circle intersecting NTS is the observer’s meridian. The fundamental direction is from $O$ to $N$.

A point on the sky $P$ has two coordinates: altitude or elevation $e$ or $\angle QOP$ and azimuth $a$ $\angle NOQ$. Astronomers sometimes use the zenith angle $z$ instead of altitude.

Stars, planets, the sun and the moon all go though a diurnal motion in this coordinate system. Stars take 23 hours 56 minutes 4.1 seconds between two successive meridian crossings. This duration is called the sidereal day. The sidereal day is getting longer by 0.0015 seconds every century as the spin of the Earth is slowing down.

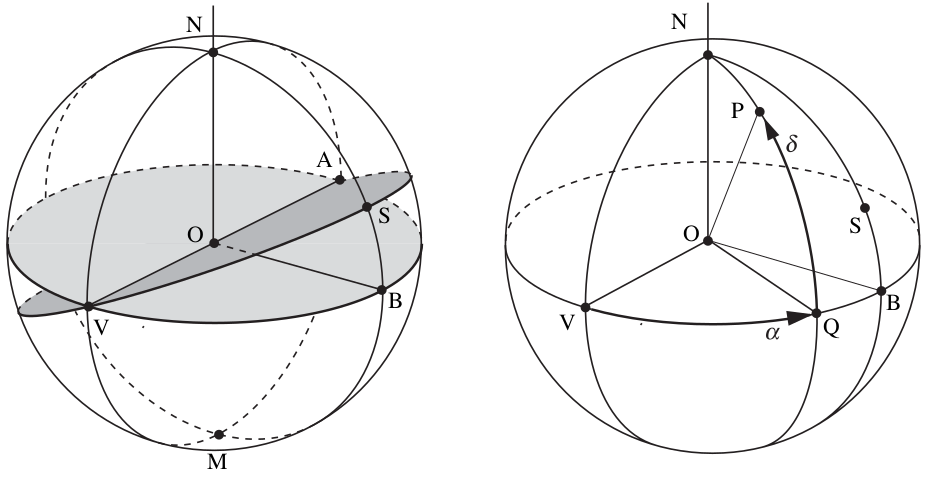
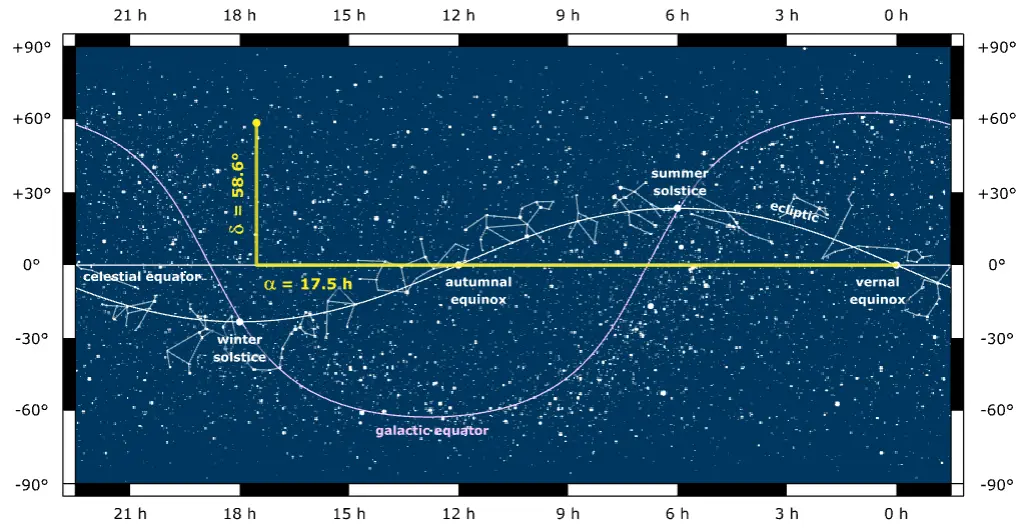
In the equatorial system, the center of the Earth is the origin $O$ and the equator is the fundamental plane making the $z$-axis parallel to the rotational axis and directly relating the celestial poles (N and M) with the terrestrial ones. The great circle created by the intersection of the fundamental plane and the celestial sphere is the celestial equator VBA. The latitude-like angles from the equator is called the declination $\delta$.

The sun traces a great circle in the celestial sphere called the ecliptic VSA which intersects the celestial equator at an angle $\epsilon=23.5$ degrees called the obliquity of the ecliptic. The point that the sun crosses going from south to north is is called the March equinox V and the direction from the center to the equinox OV is the reference direction of this system. The right ascension (RA) $\alpha$ is measured in the equatorial plane from west to east as shown in the right-handed system (right panel) above.

RA is measured in hours-minutes-seconds whereas DEC is measured in degrees-arcminutes-arcseconds. Note that ‘minute’ is a unit of time whereas ‘arcminute’ is a pseudo-unit of angle.

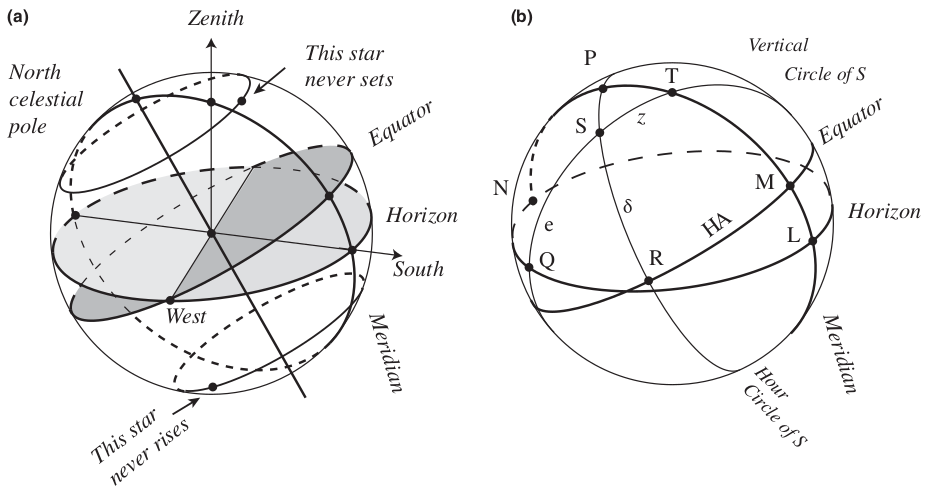
The relation between the equatorial and horizon systems is shown above. It assumes an observer located at a latitude of $60$ degrees north on Earth. Both spheres show the horizon, equator and observer’s meridian, the north celestial pole P and the zenith T. Panel (a) shows the diurnal path of a circumpolar star that never sets and the path of a star that never rises for the observer at the center of the horizon.

The following equations can all be derived geometrically from the above diagram.

1. Altitude of NCP = Geodetic latitude of observer
2. Object HA = Meridian RA - Object RA
3. Sidereal day = Time between upper meridian transits of the March equinox
4. Sidereal time = Object RA on the upper meridian
5. Object HA = Sidereal time now - sidereal time when the object culminates

The equatorial system is not inertial, it is accelerated due to the long-term general precession and short-term oscillatory nutation.

As shown above, the north ecliptic pole remains fixed with respect to the stars, but the north celestial pole rotates in a small circle around the ecliptic pole. The precessional circle has a radius of around 23 deg, the same as the obliquity of Earth’s axis. Obliquity is the angle between the celestial and ecliptic axes.

NCP completes one orbit in 26,000 years moving at an almost constant speed. So the celestial equator moves at an almost constant speed westward toward ecliptic at a rate of $5029.097$ arcsec (1.4 deg) per century, i. e. almost $50''$ per year.

Hipparchus already knew about precssion. Polaris was not always so close to the NCP. Around 4500 years ago, Thuban was the pole star. After 12,000 years, Vega will be the pole star and Polaris will have a declination of $45$ degrees.

Unlike the lunisolar precession, planetary precession causes the obliquity, i. e. distance between the ecliptic and celestial axes, to change. It results in an oscillation on top of the precessional circle as shown above. The obliquity oscillates between $22^\circ$ and $24^\circ$ once in 41,000 years. Currently the obliquity is decreasing by $47''$ per century, i. e. only $0.47''$ per year.

The actual reasons behind these motions lies in the physics of a spinning top. When you release a top, you exert a torque on the axis of the top and, hence, the axis rotates and oscillates. The details can be found in this Universe article.

The equatorial system is highly non-inertial, has a lot of different accelerations. Four effects, specially, change the standard J2000 equatorial RA-DEC of an astronomical object: (1) precession, (2) nutation, (3) heliocentric stellar parallax, and (4) aberration of starlight. Parallax is caused by the changing position of Earth as it goes around the sun. Aberration is caused by the changing velocity of Earth. We have already talked about these 4 effects.

In order create a more inertial frame of reference, IAU recommended ICRS (International Celestial Reference System) in 1991. The origin of ICRS is the barycenter of the solar system. The equator still defines the fundamental plane, but the poles and the axis are determined by distant quasars.

RA and DEC are traditionally measured using transit telescopes (or meridian circles). A transit telescope always points toward an observer’s meridian and rotates east-west. To determine declinations, first locate the celestial pole and take a circumpolar star. Then read the graduated circle twice: once when the star crosses the upper meridian, once when it crosses the lower meridian. The average of the two gives the location of NCP or SCP on your meridian circle. After this calibration, any other declination can be determined.

The position of Alpha Centauri is uncertain in ICRS by only 0.4 mas (milli-arcsec), i. e. by only 3 parts in $10^9$ of a full circle, but its distance is uncertain by one part in 2500.

ICRS-defining quasars have positional uncertainty of only 0.02 mas, but distance uncertainty of almost 10%.

Semimajor axis of planetary orbits

$$ a = P^{2/3} $$

where $a$ is measured in AU, and $P$ the period in years.

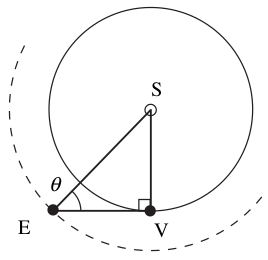
$$ 1 \text{ au } = \frac{c\Delta t}{2\cos\theta} = 149.5978 \text{ Gm} \pm 1 \mu\text{m}$$

where $\Delta t$ is the time it takes for a radio signal to come back to earth after getting reflected from Venus.

TAI: International Atomic Time defines 1 SI second as 9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the cesium-133 atom. Practical atomic clocks have a precision of about $2/10^{13}$. Two clocks located at two frames will have differing speed based on their relative velocities (special relativity) and their accelerations or local gravitational fields (general relativity).

A astronomical day = 86,400 SI seconds. But historically we have used the sun, not atoms, for measuring time.

This figure shows an Earth-sized clock from god’s-eye-view from above the solar system. Figure (b) clearly shows that Local apparent solar time = HA of the Sun + 12 hrs. The apparent solar day varies from the astronomical day throughout a year because of Earth’s obliquity of axis and ellipticity of orbit. So we introduce the

Local mean solar time = HA of the mean Sun + 12 hrs.

Equation of time = local apparent solar time - local mean solar time. It takes on values up to $\pm 15$ minutes in a year.

Universal time, UT = mean solar time at Greenwich.

But even UT is not precise enough because Earth’s precession is not that accurately known and also because its spin is not uniform. Variations in spin are caused by the tidal effects of the moon (monthly) and the sun (seasonal). Even the interaction between the core and the mantle of earth changes the spin on timescales of decades. Finally, tidal friction is slowing the spin rate and, hence, the mean solar day is getting longer by $1.5$ milliseconds per century, or $15$ $\mu$s per year.

IERS maintains UTC: Coordinated Universal Time (UTC). UTC is close to UT, but it uses SI seconds instead of mean solar time. To keep pace with UT, UTC introduces leap seconds occasionally. The acceleration Earth’s spin has a random component, so it is not possible to predict the need for leap seconds ahead of time. Between 1972 and 1998, a total of 22 leap seconds were added.

Our legal time follows UTC but finds

Zone time = UTC + longitude correction for the zone.

The zones are usually $15^\circ$ wide in longitude; as the earth rotates that much in 1 hour. Computer networks synchronize clocks using standard protocols like ITS and ACTS.

Sidereal time = HA of the mean March equinox of date

which follows the UT. Astronomers count days continuously from a reference day as

Julian date (JD) = number of elapsed UT days since 4713 BC January 1.5 (12 hrs UT).

In many cases, JD is given instead of UT date.

J2000.0 = Julian epoch 2000.0 = 2000 Jan 1.5 UT = JD 2451545.0.

Space velocity

$$ \vec{v} = \vec{v}_T + \vec{v}_R $$

where $\vec{v}_T$ is the tangential velocity and $\vec{v}_R$ the radial velocity.

Radial velocity can be measured directly using a spectrograph or spectrometer.

Tangential velocity can only be calculated from the measurements of displacement or proper motion.

Measure the ICRS coordinate of a star in 10-year intervals. If the position changes, we know that the star actually moved because ICRS is not affected by parallax or precession.

Christian Doppler gave a lecture on 25 May 1842 at the Royal Bohemian Scientific Society in Prague, Czechia.

For small redshifts $z\ll 1$

$$ \frac{\lambda-\lambda_0}{\lambda_0} = \frac{\Delta \lambda}{\lambda_0} = \frac{v_R}{c} = z $$

Resolving power of a spectrograph

$$ R = \frac{\lambda}{\delta\lambda} $$

For large redshifts $z \gg 1$

$$ z = \frac{\sqrt{1-\beta^2}}{1-\beta}-1 $$

where

$$ \beta = \frac{v_R}{c} = \frac{(z+1)^2-1}{(z+1)^2+1} $$