Overthrowing Ptolemy

Astronomy has almost 3000 years of continuous history where almost all cultures of the world contributed. In this module, we will see how our view of the universe changed due to the observational works of astronomers and how this endeavor gave rise to modern science. Our main goal is to understand the importance of ‘telescopes’ in this astronomical journey as a motivation for this course because the course is about modern telescopic observations.

Before Ptolemy, a Greek astronomer and mathematician of Alexandria, people measured positions of stars and planets for more than a thousand years. Ptolemy combined all these information and presented a coherent model of the cosmos in his 2nd-century book Almagest (‘al majisti’ or ‘the greatest’ in Arabic).

In this model, earth is at the center of the universe and all objects of the sky move around the earth. The whole sky seems to rise and set on a daily basis giving the diurnal motion. And seven objects (Sun, Moon, Mercury, Venus, Mars, Jupiter and Saturn) have an additional ‘annual’ motion: they change their position with respect to the background stars from one day to the next.

Try to understand the ‘annual’ motion this way. If you measure the position of Mars at exactly 10 pm every night for 687 days, you will see that the position changes from one day to the next. The position tonight at 10 pm will be the same as the position exactly after 687 days at 10 pm. This does not happen to the stars; the position of a star is the same every night on a give time. But Mars keeps moving on the background of stars and comes back to its initial position after every 687 days.

How do you interpret this behavior? Aristotle imagined 8 concentric spheres around the earth:

the outermost sphere has all the stars, the inner 7 spheres contain the heavenly bodies Saturn, Jupiter, Mars, Sun, Venus, Mercury and the Moon. Each of the 8 spheres moves once in 24 hours, but the 7 inner spheres have a second annual motion. For the sphere of Mars, the annual motion repeats after every 687 days. The sphere of moon takes around a month to come back to its initial position, the spheres of Sun, Mercury and Venus take around 1 year, Jupiter’s sphere takes 12 years and Saturn’s sphere around 29 years.

So far it seems like a neat theory. Every movement is described by a ‘uniform circular motion’ as Plato envisaged, even though there is no explanation of exactly how the spheres move. But 4 planets (Venus, Mars, Jupiter, Saturn) made the life of ancient astronomers very difficult. These planets have something called ‘retrograde motion’ shown in the following figure.

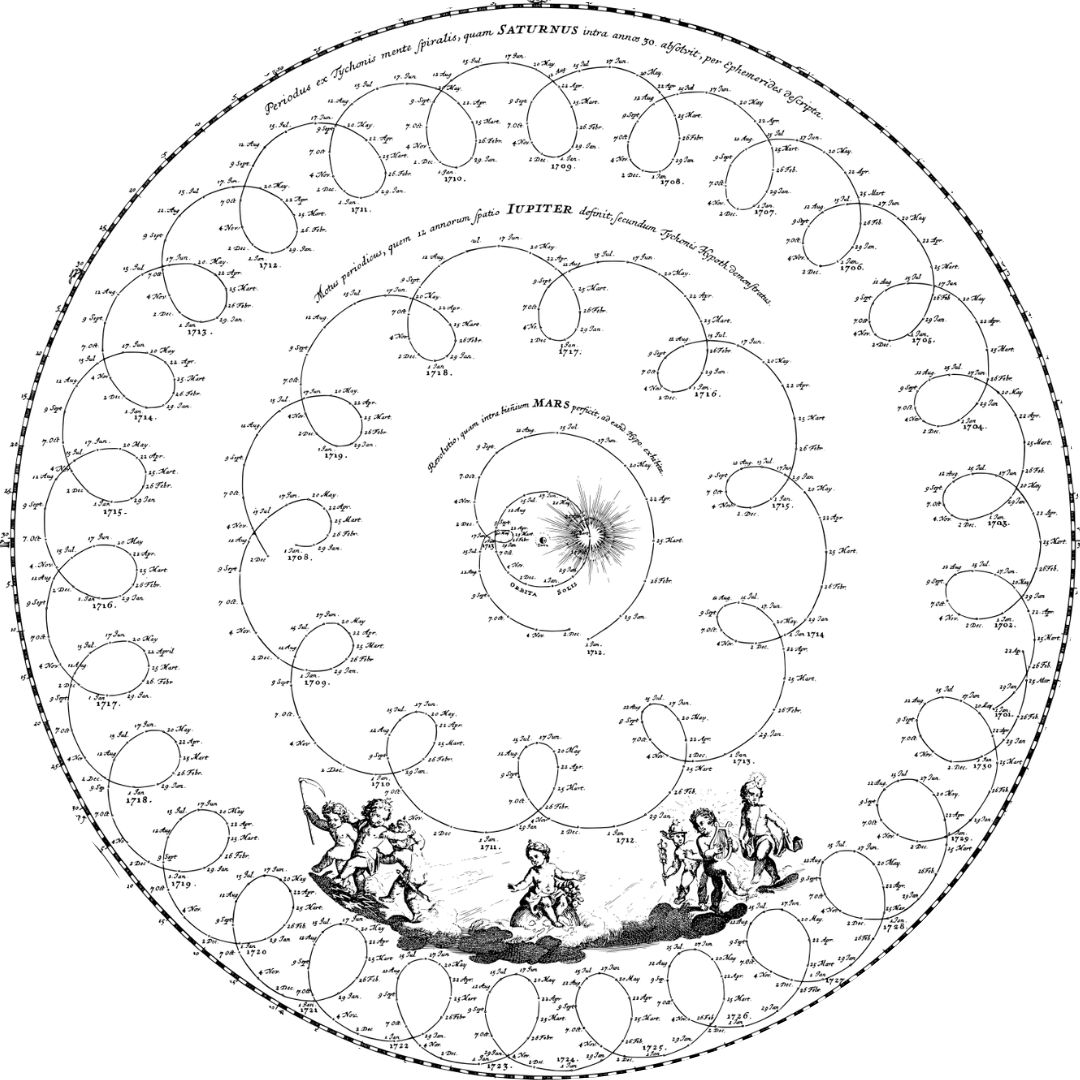
For example, during its 12 year long ‘annual’ motion, Jupiter changes course as many as 11 times. During these ‘retrograde’ periods, Jupiter seems to be moving backward from one day to the next, but the period passes and the initial prograde motion is re-established. After a year, the retrograde period comes back. How many times Saturn does this? Count!

To describe these irregularities, Ptolemy followed his predecessors Apollonius and Hipparchus and used something called ‘epicycle’ in a new model. In this model, each planet orbits on a small circle called epicycle and the center of the epicycle in turn rotates around the earth. The animation below (made using NAAP Labs) shows how.

This model had quite a few ‘free parameters’ that could be adjusted to describe the motion of any planet, for example, the radius of the epicycle and the speed of the planet along the epicycle. Ptolemy had to move the earth from the center a little bit as well anticipating the ellipse of Kepler.

But even after all these tweaking, the exact position of the planets could not be predicted. In 5th-century India, Aryabhata found problems in Ptolemy. Later, astronomers in the Islamic world made more precise and accurate observations which further disclosed the limitations of the model.

A timid monk in Poland named Copernicus came to the rescue. Maybe he could dare to put the sun at the center because he had some vague knowledge about the heliocentric adventures of Aristarchus in ancient Greece. His model was published in the 1543 book On the Revolutions which literally sowed the seeds of ‘scientific revolution’ in Europe. The following figure is taken from this book.

As you can see, the sun is at the center and the outermost sphere is for the fixed stars. In the middle, the six planets are given the spheres from II to VII and moon is put on an orbit around the earth. We see the whole sky rise and set every day because earth rotates on its axis once in 24 hours. We see the annual motions because the planets are orbiting around the sun. The annual motion of the sun takes 1 year because the earth moves around the sun once in 1 year. Mercury and Venus also take around a year because they are always close to the sun from our point of view. Mars, Jupiter and Saturn take approximately 2, 12 and 29 years because those are exactly how long they take to orbit the sun once.

Sounds good. But how did the heliocentric model solve the problem of retrograde motion of the planets. Its solution was much more simple and elegant than that of the geocentric model. The video explains.

As you can see, the retrograde motion occurs every time the earth overtakes a planet in its orbit. Mars goes into retrogression only once because earth overtakes mars only once during one orbit of mars (which is less than 2 years). For Jupiter we get 11 retrogressions because earth overtakes Jupiter that many times during one orbit of Jupiter. It is no different than seeing a forward-moving bus apparently go backward when you overtake it on the road.

Kepler’s third law states that the square of the period ($T=2\pi r/v$) of a planet is proportional to the cube of its distance ($r$) from the sun. This entails there is a centripetal acceleration ($v^2/r$) proportional to the inverse-square of the distance which was found by Newton later.

$$ T^2 \propto r^3 \Rightarrow \left(\frac{r}{v}\right)^2 \propto r^3 \Rightarrow \frac{v^2}{r} \propto \frac{1}{r^2} $$

Kepler’s third law states that a planet sweeps out equal areas (subtended by an arc at the focus with the sun) in equal times. This entails $dA/dt$ is a constant which was later found to be related to the magnitude of the angular momentum ($J$) of the planet which is always conserved.

$$ \frac{dA}{dt} = \frac{J}{2m}. $$

Newton formulated this into his third law of motion. Galileo did not pay much attention to Kepler and, hence, missed out on the theoretical aspects of astronomy. He instead focused on observations and found two observations supporting Copernicus although they did not prove heliocentrism conclusively.

Here you see the positions of more than 80 stars in the belt and sword of Orion seen by Galileo through his telescope. With a telescope Galileo could magnify planets, but the stars never appeared magnified. There could only be one explanation: the stars must be extremely distant. This supports Copernicus because if the stars were not distant, an observer on the moving earth would see their position change due to parallax.

Planets indeed appeared larger through Galileo’s eyepiece and he discovered 4 satellites orbiting around the planet Jupiter as you see here in the observations done in January 1610. Galileo has drawn the changing positions of the moons (dots beside the circle) around Jupiter. This supported Copernicus because for the first time we get proof of revolution around an object other than the earth.

Descartes went one step further and made all the stars in the night-sky equals of the sun. In his ‘mechanical’ model of the universe there is a vortex of material around each star and the planets move around a star because of their interaction with the material. This was the first ‘physical’ model of the solar system as opposed to the merely ‘mathematical’ models of Ptolemy, Copernicus and Kepler.

Newton made gravity the physical reason behind planetary motions as opposed to Descartes’ mysterious vortices. The full form his gravitational acceleration

$$ \vec{g} = \frac{GM}{r^2} \hat{r} $$

where $G$ is the Newtonian gravitational constant, $M$ the mass of an object and $r$ is the distance at which the acceleration is being calculated. This $\vec{g}$ can be thought of also as a gravitational field around a massive object. The gravitational potential

$$ U = - \frac{GMm}{r} $$

for a small mass $m$ around a large mass $M$.

The theory was later modified by Einstein as

$$ G_{\mu\nu} + \Lambda g_{\mu\nu} = \kappa T_{\mu\nu} $$

where $G_{\mu\nu}$ is the Einstein tensor, $g_{\mu\nu}$ is the metric tensor, $T_{\mu\nu}$ is the stress-energy tensor, $\Lambda$ is the cosmological constant and

$$ \kappa = \frac{8\pi G}{c^4} $$

is the Einstein gravitational constant.

The heliocentric theory was finally proved by two observations: the observation of stellar aberration of $\gamma$ Draconis by James Bradley in 1727 and the observation of stellar parallax of Vega by von Struve.

In this example of 2D frame moving only in the $x$-direction, the vertical component of the apparent speed of light ($u$) will not change, but the horizontal component will be modified due to the velocity of the Earth.

$$ \tan\phi = \frac{u_y'}{u_x'} = \frac{u_y}{\gamma(u_x+v)} $$

where $\gamma=(1-v^2/c^2)^{-1/2}$, $v$ is the velocity of the observer and $c$ is the magnitude of the velocity of light. The velocity components of light in the rest and moving frames are $(u_x,u_y)$ and $(u_x',u_y')$, respectively and $c^2 = u_x^2 + u_y^2$. So

$$ \tan\phi = \frac{c\sin\theta}{\gamma(c\cos\theta+v)} = \frac{\sin\theta}{\gamma(v/c+\cos\theta)}. $$

If $v \ll c$, $\gamma=1$. and if $\theta=90^\circ$ then

$$ \tan(\theta-\phi) = \cot\phi = \frac{\gamma(v/c+\cos\theta)}{\sin\theta} = \frac{v}{c} $$

and, finally, if $\theta-\phi$ is very small then aberration $\alpha = \theta-\phi \approx v/c$.

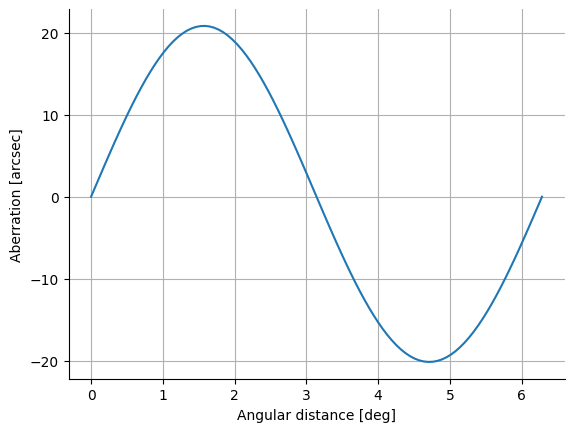
Using google colab, calculate the factor $v/c$ considering $v$ to be the speed of earth around the sun which is $30$ km/s. You will see that $v/c\approx 20$ arcsec. So the maximum stellar aberration is 20 arcsec, but the actual measurement of aberration will vary from $-20$ to $+20$ arcsec for starlight coming at a right angle with the plane of the solar system.

The annual variation of aberration can be seen in the figure above. Around the time of March equinox, the Earth is travelling toward left in this figure, so starlight is also bent toward the left, but as the Earth approaches the June solstice, the aberration vanishes and then again increases as the Earth travels toward the September equinox. The aberration again goes to zero around the time of December solstice.

This variation has been modelled above using a sine function with an amplitude of $20$ arcsec and a period of $2\pi$. The amplitude is not exactly $20$ and the sine curve is not vertically symmetric because the variation of the orbital velocity of the Earth in its elliptical orbit has been taken into account here. Click on the image to see the python code and the corresponding equations.

Compare this model with the actual observations carried out by James Bradley in 1727 using the star $\gamma$ Draconis.

You can see minimum aberration during the solstices and maximum aberration during the equinoxes as predicted. Think why!

The tangent of the parallactic angle

$$ \tan p = \frac{a}{r} $$

where $r$ is the distance to the object and $a$ is in au. For $p\ll 1$ we can approximate $\tan p = \sin p = p$ and

$$ p = \frac{a}{r}. $$

If $a$ is in au and $p$ in arcsec, then $r$ is in parsec.

1 parsec = 206265 au = $3.085678\times 10^{16}$ m = 3.261633 ly.

For nearby star, measurements of $p$ have uncertainties of 50 mas, but can be reduced to 5 mas. Only works for around 1000 stars closer than 20 pc.

<gallery full> :courses:ast201:vonstruve.png Bessel 1838 :courses:ast201:bessel.png von Struve 1837 :courses:ast201:parallax-henderson.png Henderson 1837 </gallery>

HIPPARCOS has parallax uncertainties of 0.97 mas for around 118k stars brighter than $m_V=8.0$.

1. Bradley 1727, A Letter from the Reverend Mr. James Bradley.
2. Reid & Menten, 2020, The First Stellar Parallaxes Revisited.
3. Warner, 2004, Thomas Henderson and α Centauri.