প্লাজমা

আগে জিওফিজিক্সের বিষয় ছিল মূলত পৃথিবীর ইন্টেরিয়র, কিন্তু এখন পৃথিবীর এটমস্ফিয়ার ও নেবারহুডও এই ফিজিক্সের মধ্যে স্টাডি করা হয়। আমাদের নেবারহুডের বা আসলে পুরা সোলার সিস্টেমের পদার্থ কঠিন, তরল, বায়বীয় কোনোটাই না, বরং প্লাজমা অবস্থায় আছে। আসলে ইউনিভার্সের মোট পদার্থের ৯৯ পার্সেন্টই প্লাজমা। তাই প্লাজমা কি তা বুঝা স্পেস ফিজিক্সের জন্য জরুরি।

প্লাজমা হলো চার্জড পার্টিকেলের একটা আয়নিত গ্যাস যেখানে ফ্রি পজিটিভ ও নেগেটিভ চার্জ ক্যারিয়ার আছে সমান সমান। এই কারণে স্টেশনারি অবস্থায় প্লাজমা কোয়াজাইনিউট্রাল ধরা হয়। বাইরে থেকে একে নিউট্রাল মনে হয়। আর ফ্রি পার্টিকেল তাকেই বলে যার পটেনশাল এনার্জির চেয়ে কাইনেটিক এনার্জি বেশি। এই কারণে প্লাজমার টেম্পারেচারও বেশি, কারণ টেম্পারেচার কাইনেটিক এনার্জির পরিমাপ।

স্টেশনারি অবস্থায় প্লাজমা যাতে কোয়াজাইনিউট্রাল হয়, সেজন্য মাইক্রোস্কোপিক স্কেলে এক কণাদের চার্জ এমনভাবে ক্যান্সেল হতে হবে যাতে ম্যাক্রোস্কোপিক স্কেলে গ্যাসটাকে নিউট্রাল মনে হয়। একটা চার্জ $q$ থেকে $r$ দূরত্বে কুলম্ব পটেনশাল

$$ \phi_C = \frac{q}{4\pi\epsilon_0 r} $$

যেখানে $\epsilon_0$ ফ্রি স্পেসে পার্মিটিভিটি। এই পটেনশালের মধ্যে যাতে অন্য চার্জের পটেনশালের প্রভাব পড়তে না পারে সেজন্য এটাকে শিল্ড করতে হবে। এই শিল্ডেড পটেনশালের নাম ডেবাই পটেনশাল, গাণিতিকভাবে

$$ \phi_D = \frac{q}{4\pi\epsilon_0 r} e^{-r/\lambda_D} $$

যেখানে $\lambda_D$ কে বলে ডেবাই লেন্থ। একটা চার্জের ডেবাই লেন্থের বাইরে, মানে $r > \lambda_D$ হলে, পটেনশাল কমতে থাকে এক্সপোনেনশালি। থার্মাল কাইনেটিক এনার্জি নিউট্রালিটি কমাতে চায়, ইলেক্ট্রোস্ট্যাটিক পটেনশাল এনার্জি নিউট্রালিটি আবার ফেরাতে চায়, এবং ডেবাই লেন্থে এই দুই এনার্জির মধ্যে একটা ভারসাম্য তৈরি হয়। ডেবাই লেন্থ

$$ \lambda_D = \left(\frac{\epsilon_0 k_B T_e}{n_e e^2}\right)^{1/2} $$

যেখানে $k_B$ বোল্টজমান কনস্টেন্ট, $e$ ইলেক্ট্রনের চার্জ, $T_e$ ইলেক্ট্রনের টেম্পারেচার যা আয়ন টেম্পারেচার $T_i$-এর সমান, $n_e$ ইলেক্ট্রনের ডেন্সিটি যা আয়ন ডেন্সিটি $n_i$-এর সমান। টেম্পারেচারের সংজ্ঞা আরো একজাক্ট করা যায়, কিন্তু আমরা এভারেজ এনার্জি ও টেম্পারেচারের মধ্যে এই সম্পর্কটাই আপাতত ধরে নিব: $\langle E \rangle = k_B T$।

কোয়াজাইনিউট্রাল হতে হলে একটা প্লাজমার ফিজিকেল লেন্থ ডেবাই লেন্থের চেয়ে অনেক বেশি হতে হবে, শর্তটা হলো $L \gg \lambda_D$। এই শর্ত পূরণ না হলে সব চার্জের যৌথ শিল্ডিং কাজ করবে না। এই শর্তকে তাই অনেক সময় প্রথম প্লাজমা ক্রাইটেরিয়ন বলে।

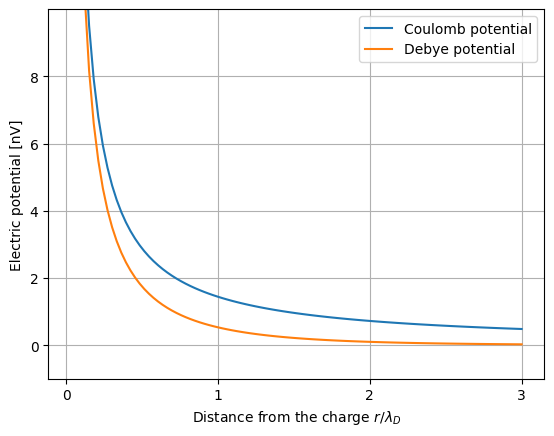
এই ফিগারে কুলম্ব ও ডেবাই পটেনশাল তুলনা করা হয়েছে ন্যানোভোল্ট ইউনিটে। এক্স অক্ষে দূরত্ব দেয়া হয়েছে ডেবাই লেন্থের অনুপাতে। দেখা যাচ্ছে, ডেবাই লেন্থের বাইরে কুলম্ব পটেনশালের (নীল) তুলনায় ডেবাই পটেনশাল (অরেঞ্জ) অনেক তাড়াতাড়ি শূন্যের কাছাকাছি চলে যাচ্ছে।

ডেবাই লেন্থের রেডিয়াস দিয়ে একটা ডেবাই স্ফিয়ার চিন্তা করা যায়। প্লাজমা হতে হলে এই স্ফিয়ারের মধ্যে যথেষ্ট সংখ্যক পার্টিকেল থাকতে হবে। স্ফিয়ারটার ভলিউম $(4\pi/3) \lambda_D^3$ যাকে ইলেক্ট্রন ডেন্সিটি দিয়ে গুণ করলে মোট পার্টিকেলের সংখ্যা হয়

$$ N = \frac{4\pi}{3} \lambda_D^3 n_e $$

যার মধ্যে $\Lambda = \lambda_D^3 n_e$ কে বলা হয় প্লাজমা প্যারামিটার। এখান থেকেই আসে দ্বিতীয় প্লাজমা ক্রাইটেরিয়ন:

$$ \Lambda \gg 1 $$

অর্থাৎ মোট পার্টিকেল একের চেয়ে অনেক বেশি হতে হবে। এই ইকুয়েশনে ডেবাই লেন্থের ফুল ফর্ম বসালে পাওয়া যায়

$$ n_e^{1/3} \ll k_B T_e $$

যা দ্বিতীয় ক্রাইটেরিয়নের অর্থ পরিষ্কার করে। পটেনশাল এনার্জি যেহেতু উপরের ইলেক্ট্রন ডেন্সিটির সমানুপাতিক, সেহেতু বলা যায়, মিন পটেনশাল এনার্জিকে মিন এনার্জি $\langle E \rangle$-এর তুলনায় অনেক কম হতে হবে।

কোয়াজাইনিউট্রাল একটা প্লাজমাকে যখন বাইরে থেকে ডিস্টার্ব করা হয় তখন তার ইলেক্ট্রনরা আবার আগের নিউট্রাল দশায় ফিরে যেতে চায়। আয়ন না ধরে ইলেক্ট্রনের গতির কথা বলা হচ্ছে কারণ অন্যান্য আয়নের তুলনায় ইলেক্ট্রন অনেক হালকা। বাইরের ডিস্টার্বেন্সের কারণে প্লাজমার ইলেক্ট্রনদের মধ্যে একটা এভারেজ অসিলেশন তৈরি হয় তুলনামূলক ম্যাসিভ আয়নদের চারদিকে। এই অসিলেশনের কম্পাঙ্কের নাম প্লাজমা ফ্রিকোয়েন্সি, গাণিতিকভাবে

$$ \omega_{pe} = \left(\frac{n_e e^2}{m_e \epsilon_0} \right)^{1/2} $$

যেখনে $m_e$ ইলেক্ট্রনের ম্যাস। এই ইকুয়েশনের মূল শিক্ষা হলো, প্লাজমা ফ্রিকোয়েন্সি ইলেক্ট্রন ডেন্সিটির বর্গমূলের সমানুপাতিক।

পৃথিবীর আয়নোস্ফিয়ারের মতো প্লাজমাকে বিশুদ্ধ প্লাজমা বলা যায় না। আয়নোস্ফিয়ারে ফ্রি পার্টিকেলের পাশাপাশি অনেক নিউট্রাল এটম আছে। নিউট্রালদের সাথে ফ্রি চার্জের অনেক কলিশন হলে দুয়ের মধ্যে একটা ভারসাম্য তৈরি হয় এবং প্লাজমাটা তখন নিউট্রাল গ্যাসের মতো আচরণ করে। এটা ঠেকানোর জন্য ইলেক্ট্রনদেরকে কলিশন থেকে বিরত থাকতে হবে। এই শর্তকে কেন্দ্র করে বানানো হয়েছে তৃতীয় প্লাজমা ক্রাইটেরিয়ন:

$$ \omega_{pe} \tau_n \gg 1 $$

যেখানে $\tau_n$ ইলেক্ট্রন ও নিউট্রালের মধ্যে দুইটা কলিশনের মধ্যবর্তী এভারেজ সময়। এর মূলকথা এই: প্লাজমা ফ্রিকোয়েন্সিকে হতে হবে কলিশন ফ্রিকোয়েন্সির চেয়ে অনেক বেশি।

প্লাজমা ডায়নামিক্স মানে বিভিন্ন ধরনের চার্ক ক্যারিয়ারের সাথে ইলেক্ট্রিক ও ম্যাগ্নেটিক ফিল্ডের ইন্টারেকশন। স্পেস প্লাজমায় বাইরের প্রভাবের পাশাপাশি প্লাজমার ভিতরেও অনেক ধরনের প্রভাব থাকে, এই কারণে এর ডায়নামিক্স অনেক জটিল। এর পারফেক্ট গাণিতিক মডেল তৈরি করতে হলে প্রত্যেক পার্টিকেলের গতির ইকুয়েশন জানতে হবে, এবং প্রতিটা পার্টিকেল যেহেতু অন্য সব পার্টিকেল দিয়ে প্রভাবিত সেহেতু সব পার্টিকেলের ইকুয়েশন একসাথে সল্ভ করতে হবে। এটা বাস্তবে অসম্ভব এবং অত জরুরিও না, কারণ আমরা শুধু প্লাজমার এভারেজ বৈশিষ্ট্য জানতে চাই। তাই চার ধরনের এপ্রক্সিমেশন বা সিম্পলিফায়িং এপ্রোচ ব্যবহার করা হয় প্লাজমা থিওরি বানানোর জন্য।

সিংগল পার্টিকেল মোশন সবচেয়ে সিম্পল এপ্রোচ। এখানে শুধু একটা স্বতন্ত্র পার্টিকেলের উপর বাইরের ইলেক্ট্রিক ও ম্যাগ্নেটিক ফিল্ডের প্রভাব বিবেচনা করা হয়। এখানে প্লাজমার সার্বিক আচরণ নেগ্লেক্ট করা হয়। কিন্তু রিং কারেন্টে যে-ধরনের লো-ডেন্সিটি প্লাজমা পাওয়া যায় তা ব্যাখ্যার জন্য এই এপ্রোচই যথেষ্ট।

ম্যাগ্নেটোহাইড্রোডায়নামিক্স হলো অন্য এক্সট্রিমে, যেখানে স্বতন্ত্র পার্টিকেল বাদ দিয়ে সার্বিকভাবে পুরো প্লাজমাটা বিবেচনা করা হয়। প্লাজমাটা এখানে একটা একক পরিবাহী ফ্লুয়িড যার কিছু এভারেজ প্রপার্টি আছে, যেমন, ডেন্সিটি, টেম্পারেচার, ভেলোসিটি। এখানে প্লাজমাটা লোকাল ইকুয়িলিব্রিয়ামে আছে ধরা হয়। অনেক পরিবাহী ম্যাগ্নেটিক ফ্লুয়িডে কম কম্পাঙ্কের তরঙ্গ স্টাডি করার জন্য এই এপ্রোচ ভালো।

মাল্টি-ফ্লুয়িড এপ্রোচ ম্যাগ্নেটোহাইড্রোডায়নামিক্সের মতোই, শুধু এখানে বিভিন্ন প্রজাতির পার্টিকেল আলাদা আলাদাভাবে বিবেচনা করা হয়, যেমন, ইলেক্ট্রন, প্রোটন, আরো ভারী আয়ন। প্রত্যেক প্রজাতির জন্য একটা আলাদা ফ্লুয়িড বরাদ্দ করা হয়।

কাইনেটিক থিওরি সবচেয়ে উন্নত এপ্রোচ, কারণ এখানে স্ট্যাটিস্টিক্স ভালোভাবে ইউজ করা হয়। স্বতন্ত্র পার্টিকেলের গতির ইকুয়েশনের বদলে কাজে লাগানো হয় ফেজ স্পেসে বিভিন্ন ধরনের স্ট্যাটিস্টিকেল ডিস্ট্রিবিউশন ফাংশন।