ম্যাগ্নেটিক ডাইপোল ফিল্ড
পৃথিবীর সার্ফেসের কাছাকাছি অঞ্চলে ম্যাগ্নেটিক ফিল্ড ডাইপোলার হিসেবে চিন্তা করা যায়, দক্ষিণ থেকে উত্তর মেরুর দিকে। ফিল্ড লাইনের চারদিকে অনেক চার্জিত কণা উত্তর-দক্ষিণে জাইরেট ও অসিলেট করে, এবং পূর্ব-পশ্চিমে ড্রিফট করে। পৃথিবীর ইনার কোর, আউটার কোর, কনভেকশন কারেন্ট ও ম্যাগ্নেটিক ফিল্ড লাইন নিচে দেখানো হয়েছে।

ম্যাগ্নেটিক ফিল্ডটা তৈরি হয় পৃথিবীর আউটার কোরে লিকুইড মেটালের গতির কারণে। সলিড ইনার কোরের হিটের কারণে লিকুইড আউটার কোরে কনভেকশন হয়। ইনার কোর যদি চুলা হয়, তবে আউটার কোর সেই চুলার উপরে পানির পাতিল; চুলার তাপে যেমন ফুটন্ত পানিতে বুদ্ববুদের কনভেকশন হয়, তেমনি ইনার কোরের তাপে আউটার কোরের লিকুইড মেটালের কনভেকশন হয়। পৃথিবীর রোটেশন থেকে তৈরি হওয়া করিওলিস ফোর্সের কারণে কনভেকশনটা হয় সার্কুলার পথে। লিকুইড মেটালের এই সার্কুলার গতি কারেন্ট লুপ তৈরি করে, এবং এর ফলে লুপের এরিয়া ভেক্টরের ($\mathbf{A}$) দিকে ম্যাগ্নেটিক ফিল্ড তৈরি হয়। লুপের মধ্যে দিয়ে যদি $I$ কারেন্ট প্রবাহিত হয়, তাহলে এই ফিল্ডের ম্যাগ্নেটিক ডাইপোল মোমেন্ট
$$ \vec{\mu}_E = I\mathbf{A} $$
যার এভারেজ ম্যাগ্নিচুড আমাদের হিসাব মতে $\mu_E = 8.05\times 10^{22}$ A m$^2$। এখন বিও-সাভার ল ব্যবহার করে একটা কারেন্ট লুপের কেন্দ্র দিয়ে লুপের এরিয়া ভেক্টর বরাবর তৈরি হওয়া ম্যাগ্নেটিক ফিল্ড সহজেই হিসাব করা সম্ভব।
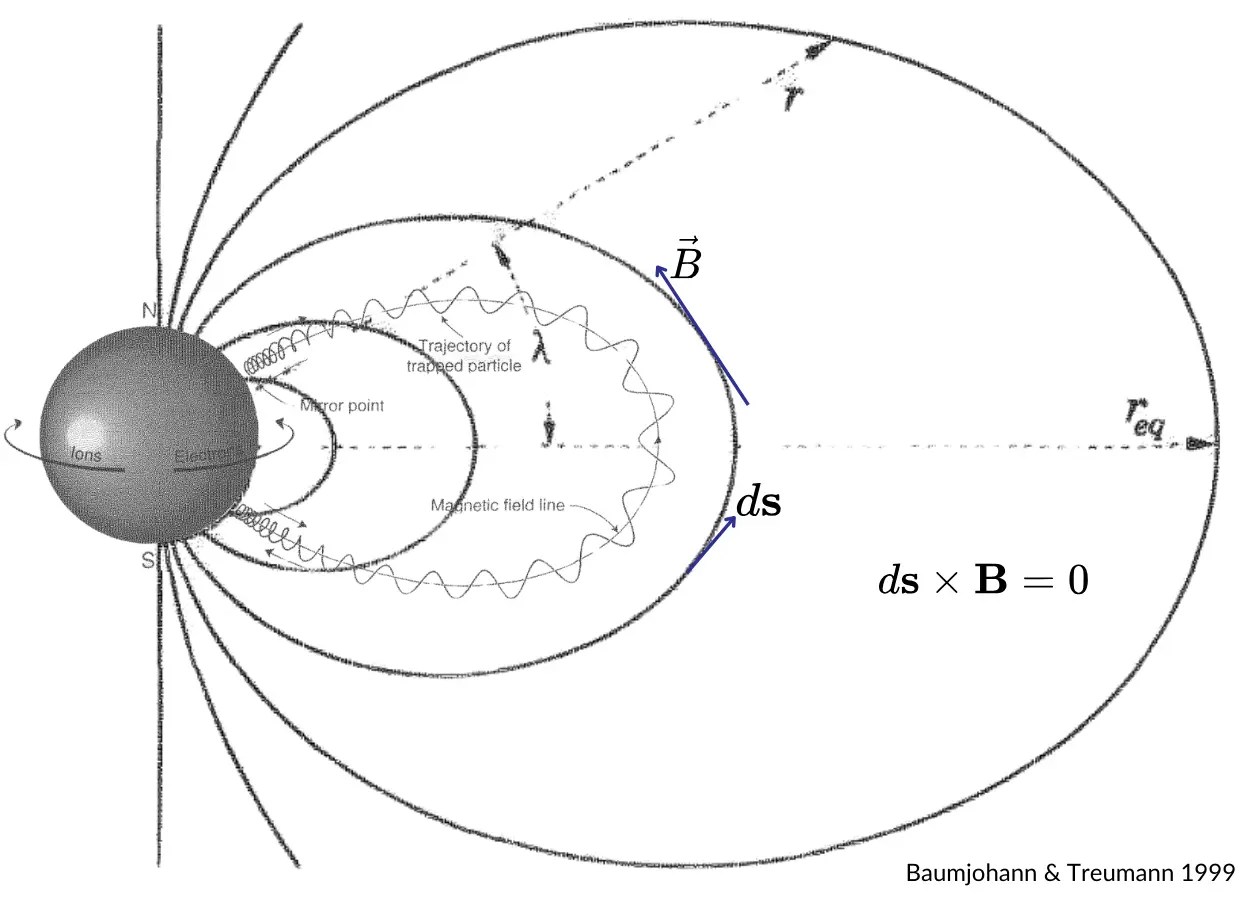
ম্যাগ্নেটিক মোমেন্ট ইউজ করে স্ফেরিকেল কোওর্ডিনেট সিস্টেমে পৃথিবীর ম্যাগ্নেটিক ফিল্ডের রেডিয়াল কম্পোনেন্ট $B_r$ এবং এজিমুথাল কম্পোনেন্ট $B_\lambda$ একসাথে এভাবে ভেক্টর হিসেবে লেখা যায়:
$$ \mathbf{B} = \frac{\mu_0\mu_E}{4\pi r^3} (-\hat{r}2\sin\lambda+\hat{\lambda}\cos\lambda) $$
যেখানে $\hat{r}$ এবং $\hat{\lambda}$ যথাক্রমে রেডিয়াল ও এজিমুথাল দিকে ইউনিট ভেক্টর; দিক দুটি উপরের ছবিতে চিহ্নিত করা আছে। এজিমুথাল দিকের কোওর্ডিনেটকে বলা যায় ম্যাগ্নেটিক ল্যাটিচুড, যার সাথে পৃথিবীর জিওগ্রাফিক ল্যাটিচুডের পার্থক্য আছে। আমাদের ম্যাগ্নেটিক ফিল্ড এক্সিসিমেট্রিক হওয়ায় স্ফেরিকেল সিস্টেমের তৃতীয় কোওর্ডিনেট এখানে ইউজ করতে হচ্ছে না, কারণ নির্দিষ্ট একটা ল্যাটিচুডে পূর্ব-পশ্চিম বরাবর ০ থেকে ৩৬০ ডিগ্রি পর্যন্ত সবখানে ফিল্ডের মান একই।। এই ফিল্ডের ম্যাগ্নিচুড
$$ B = \sqrt{B_r^2+B_\lambda^2} = \frac{\mu_0 \mu_E}{4\pi r^3} \sqrt{1+3\sin^2\lambda} $$
যেখানে দুই কম্পোনেন্টের মান বসিয়ে হিসাব করা হয়েছে। ফিল্ড লাইনের যেকোনো পয়েন্টে ম্যাগ্নেটিক ফিল্ড সেই লাইনের সাথে ট্যাঞ্জেন্ট। অতএব $d\mathbf{s}$ যদি ফিল্ড লাইনের ইনফিনিটেসিমাল এলিমেন্ট হয়, তাহলে
$$ d\mathbf{s}\times \mathbf{B} = 0 $$
ডিটার্মিনেন্টের মাধ্যমে যা সমাধান করলে পাওয়া যাবে
$$ \frac{dr}{r} = \frac{B_r}{B_\lambda} d\lambda = -d\lambda\frac{2\sin\lambda}{\cos\lambda} $$
যা ইন্টিগ্রেট করলে শেষে পাওয়া যাবে ফিল্ড লাইন ইকুয়েশন
$$ r = r_{eq} \cos^2\lambda $$
যেখানে $r_{eq}$ ইন্টিগ্রেশন কনস্টেন্ট যার মান একটা ফিল্ড লাইনের ইকুয়েটরিয়াল রেডিয়াসের সমান, যা পৃথিবী থেকে ফিল্ড লাইনের সর্বোচ্চ দূরত্ব। এটা সহজেই বুঝা যাচ্ছে কারণ $\lambda=0$ হলে $r=r_{eq}$ পাওয়া যায়। আমরা যদি মনে রাখি
$$ ds^2 = dr^2 + r^2 d\lambda^2 $$
কারণ বৃত্তের পরিধি বরাবর আর্ক এলিমেন্ট $r d\lambda$, তাহলে ম্যাগ্নেটিক ল্যাটিচুডের সাথে একটা ফিল্ড লাইনের মোট দৈর্ঘ্যের সম্পর্ক এভাবে লেখা যায়:
$$ \frac{ds}{d\lambda} = r_{eq} \cos\lambda \sqrt{1+3\sin^2\lambda} $$
যা ল্যাটিচুডের সাপেক্ষে ইন্টিগ্রেট করলে ফিল্ড লাইনের মোট দৈর্ঘ $s$ বের করা সম্ভব।
ম্যাগ্নেটিক ফিল্ড অনেক সময় পৃথিবীর ইকুয়েটরিয়াল রেডিয়াস $R_E$ দিয়ে প্রকাশ করা হয়, তবে তার চেয়েও বেশি সুবিধা যদি এল-শেল প্যারামিটার বা এল-ভ্যালু $L=r_{eq}/R_E$ ব্যবহার করা হয়। কাজটা সোজা। পৃথিবীর ইকুয়েটর বরাবর $\lambda=0$, সুতরাং ম্যাগ্নেটিক ফিল্ড কেবল $B_E = \mu_0 \mu_E / (4\pi R_E^3)$ যা দিয়ে ম্যাগ্নেটিক ফিল্ডের সাধারণ সমীকরণ ভাগ করলে পাওয়া যাবে
$$ \frac{B}{B_E} = \frac{R_E^3}{r^3} \sqrt{1+3\sin^2\lambda} $$
যেখানে $ r = r_{eq} \cos^2\lambda $ এবং $L=r_{eq}/R_E$ বসালে পাওয়া যাবে
$$ B = \frac{B_E}{L^3} \frac{\sqrt{1+3\sin^2\lambda}}{\cos^6\lambda} $$
যা অনেক ক্ষেত্রে বেশি কাজে লাগে। এল-ভ্যালু দিয়ে ফিল্ড লাইন ইকুয়েশনও অন্যভাবে লেখা যায়:
$$ \cos^2\lambda_E = \frac{R_E}{r_{eq}} = L^{-1} $$
যেখানে $\lambda_E$ সেই ম্যাগ্নেটিক ল্যাটিচুড যেখানে একটা নির্দিষ্ট এল-ভ্যালুর ফিল্ড লাইন পৃথিবীর সার্ফেসকে স্পর্শ করে।